
网址:http://www.1010jiajiao.com/paper/timu/5159829.html[举报]
(二)揭示并认识函数与其他数学知识的内在联系.函数是研究变量及相互联系的数学概念,是变量数学的基础,利用函数观点可以从较高的角度处理式、方程、不等式、数列、曲线与方程等内容.在利用函数和方程的思想进行思维中,动与静、变量与常量如此生动的辩证统一,函数思维实际上是辩证思维的一种特殊表现形式.
所谓函数观点,实质是将问题放到动态背景上去加以考虑.高考试题涉及5个方面:(1)原始意义上的函数问题;(2)方程、不等式作为函数性质解决;(3)数列作为特殊的函数成为高考热点;(4)辅助函数法;(5)集合与映射,作为基本语言和工具出现在试题中.
参考答案
难点磁场
(1)证明:令x=y=0,得f(0)=0
令y=-x,得f(0)=f(x)+f(-x),即f(-x)=-f(x)
∴f(x)是奇函数
(2)解:1°,任取实数x1、x2∈[-9,9]且x1<x2,这时,x2-x1>0,f(x1)-f(x2)=f[(x1-x2)+x2]-f(x2)=f(x1-x2)+f(x2)-f(x1)=-f(x2-x1)
因为x>0时f(x)<0,∴f(x1)-f(x2)>0
∴f(x)在[-9,9]上是减函数
故f(x)的最大值为f(-9),最小值为f(9).
而f(9)=f(3+3+3)=3f(3)=-12,f(-9)=-f(9)=12.
∴f(x)在区间[-9,9]上的最大值为12,最小值为-12.
歼灭难点训练
一、1.解析:分类讨论当a>1时和当0<a<1时.
答案:C
2.解析:用特值法,根据题意,可设f(x)=x,g(x)=|x|,又设a=2,b=1,
则f(a)=a,g(a)=|a|,f(b)=b,g(b)=|b|,f(a)-f(b)=f(2)-f(-1)=2+1=3.
g(b)-g(-a)=g(1)-g(-2)=1-2=-1.∴f(a)-f(-b)>g(1)-g(-2)=1-2=-1.
又f(b)-f(-a)=f(1)-f(-2)=1+2=3.
g(a)-g(-b)=g(2)-g(1)=2-1=1,∴f(b)-f(-a)=g(a)-g(-b).
即①与③成立.
答案:C
二、3.解析:设2x=t>0,则原方程可变为t2+at+a+1=0 ①
方程①有两个正实根,则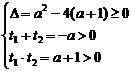
解得:a∈(-1,2-2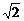
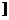 .
.
答案:(-1,2-2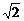
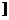
三、4.解:(1)当a=0时,函数f(-x)=(-x)2+|-x|+1=f(x),此时f(x)为偶函数;当a≠0时,f(a)=a2+1,f(-a)=a2+2|a|+1,f(-a)≠f(a),f(-a)≠-f(a).此时函数f(x)既不是奇函数也不是偶
函数.
(2)①当x≤a时,函数f(x)=x2-x+a+1=(x- )2+a+
)2+a+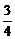 ,若a≤
,若a≤ ,则函数f(x)在(-∞,a
,则函数f(x)在(-∞,a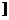 上单调递减,从而,函数f(x)在(-∞,a
上单调递减,从而,函数f(x)在(-∞,a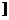 上的最小值为f(a)=a2+1.
上的最小值为f(a)=a2+1.
若a> ,则函数f(x)在(-∞,a
,则函数f(x)在(-∞,a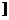 上的最小值为f(
上的最小值为f( )=
)=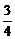 +a,且f(
+a,且f( )≤f(a).
)≤f(a).
②当x≥a时,函数f(x)=x2+x-a+1=(x+ )2-a+
)2-a+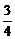 ;当a≤-
;当a≤- 时,则函数f(x)在[a,+∞
时,则函数f(x)在[a,+∞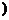 上的最小值为f(-
上的最小值为f(- )=
)=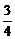 -a,且f(-
-a,且f(- )≤f(a).若a>-
)≤f(a).若a>- ,则函数f(x)在[a,+∞)上单调递增,从而,函数f(x)在[a,+∞]上的最小值为f(a)=a2+1.
,则函数f(x)在[a,+∞)上单调递增,从而,函数f(x)在[a,+∞]上的最小值为f(a)=a2+1.
综上,当a≤- 时,函数f(x)的最小值是
时,函数f(x)的最小值是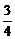 -a,当-
-a,当- <a≤
<a≤ 时,函数f(x)的最小值是a2+1;当a>
时,函数f(x)的最小值是a2+1;当a> 时,函数f(x)的最小值是a+
时,函数f(x)的最小值是a+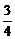 .
.
5.(1)证明:由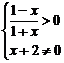 得f(x)的定义域为(-1,1),易判断f(x)在(-1,1)内是减函数.
得f(x)的定义域为(-1,1),易判断f(x)在(-1,1)内是减函数.
(2)证明:∵f(0)= ,∴f--1(
,∴f--1( )=0,即x=
)=0,即x= 是方程f--1(x)=0的一个解.若方程f--1(x)=0还有另一个解x0≠
是方程f--1(x)=0的一个解.若方程f--1(x)=0还有另一个解x0≠ ,则f--1(x0)=0,由反函数的定义知f(0)=x0≠
,则f--1(x0)=0,由反函数的定义知f(0)=x0≠ ,与已知矛盾,故方程f--1(x)=0有惟一解.
,与已知矛盾,故方程f--1(x)=0有惟一解.
(3)解:f[x(x- )]<
)]< ,即f[x(x-
,即f[x(x- )]<f(0).
)]<f(0).
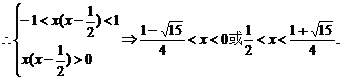
6.证明:对f(x)+f(y)=f(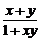 )中的x,y,令x=y=0,得f(0)=0,再令y=-x,又得f(x)+f(-x)=f(0)=0,即f(-x)=-f(x),∴f(x)在x∈(-1,1)上是奇函数.设-1<x1<x2<0,则f(x1)-f(x2)=f(x1)+f(-x2)=f(
)中的x,y,令x=y=0,得f(0)=0,再令y=-x,又得f(x)+f(-x)=f(0)=0,即f(-x)=-f(x),∴f(x)在x∈(-1,1)上是奇函数.设-1<x1<x2<0,则f(x1)-f(x2)=f(x1)+f(-x2)=f(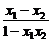 ),∵-1<x1<x2<0,∴x1-x2<0,1-x1x2>0.∴
),∵-1<x1<x2<0,∴x1-x2<0,1-x1x2>0.∴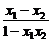 <0,于是由②知f(
<0,于是由②知f(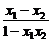 )>0,从而f(x1)-f(x2)>0,即f(x1)>f(x2),故f(x)在x∈(-1,0)上是单调递减函数.根据奇函数的图象关于原点对称,知f(x)在x∈(0,1)上仍是递减函数,且f(x)<0.
)>0,从而f(x1)-f(x2)>0,即f(x1)>f(x2),故f(x)在x∈(-1,0)上是单调递减函数.根据奇函数的图象关于原点对称,知f(x)在x∈(0,1)上仍是递减函数,且f(x)<0.
7.解:(1)因污水处理水池的长为x米,则宽为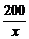 米,总造价y=400(2x+2×
米,总造价y=400(2x+2×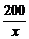 )+248×
)+248×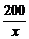 ×2+80×200=800(x+
×2+80×200=800(x+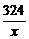 )+1600,由题设条件
)+1600,由题设条件
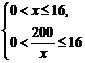 解得12.5≤x≤16,即函数定义域为[12.5,16].
解得12.5≤x≤16,即函数定义域为[12.5,16].
(2)先研究函数y=f(x)=800(x+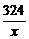 )+16000在[12.5,16]上的单调性,对于任意的x1,x2∈[12.5,16],不妨设x1<x2,则f(x2)-f(x1)=800[(x2-x1)+324(
)+16000在[12.5,16]上的单调性,对于任意的x1,x2∈[12.5,16],不妨设x1<x2,则f(x2)-f(x1)=800[(x2-x1)+324(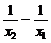 )]=800(x2-x1)(1-
)]=800(x2-x1)(1-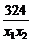 ),∵12.5≤x1≤x2≤16.∴0<x1x2<162<324,∴
),∵12.5≤x1≤x2≤16.∴0<x1x2<162<324,∴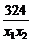 >1,即1-
>1,即1-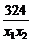 <0.又x2-x1>0,∴f(x2)-f(x1)<0,即f(x2)<f(x1),故函数y=f(x)在[12.5,16]上是减函数.∴当x=16时,y取得最小值,此时,ymin=800(16+
<0.又x2-x1>0,∴f(x2)-f(x1)<0,即f(x2)<f(x1),故函数y=f(x)在[12.5,16]上是减函数.∴当x=16时,y取得最小值,此时,ymin=800(16+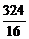 )+16000=45000(元),
)+16000=45000(元),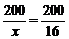 =12.5(米)
=12.5(米)
综上,当污水处理池的长为16米,宽为12.5米时,总造价最低,最低为45000元.
8.解:∵f(x)是奇函数,且在(0,+∞)上是增函数,∴f(x)在(-∞,0)上也是增函数.
又f(1)=0,∴f(-1)=-f(1)=0,从而,当f(x)<0时,有x<-1或0<x<1,
则集合N={m|f[g(θ)]<θ= ={m|g(θ)<-1或0<g(θ)<1
={m|g(θ)<-1或0<g(θ)<1 ,
,
∴M∩N={m|g(θ)<-1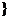 .由g(θ)<-1,得cos2θ>m(cosθ-2)+2,θ∈[0,
.由g(θ)<-1,得cos2θ>m(cosθ-2)+2,θ∈[0,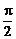 ],令x=cosθ,x∈[0,1]得:x2>m(x-2)+2,x∈[0,1],令①:y1=x2,x∈[0,1]及②y2=m(m-2)+2,显然①为抛物线一段,②是过(2,2)点的直线系,在同一坐标系内由x∈[0,1]得y1>y2.∴m>4-2
],令x=cosθ,x∈[0,1]得:x2>m(x-2)+2,x∈[0,1],令①:y1=x2,x∈[0,1]及②y2=m(m-2)+2,显然①为抛物线一段,②是过(2,2)点的直线系,在同一坐标系内由x∈[0,1]得y1>y2.∴m>4-2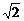 ,故M∩N={m|m>4-2
,故M∩N={m|m>4-2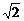 }.
}.