参考答案

难点磁场

解：由方程组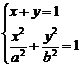消去y,整理得(a²+b²)x²－2a²x+a²(1－b²)=0　　　　　　　　　　　　　　　　　　　　　 ①

则椭圆与直线l在第一象限内有两个不同的交点的充要条件是方程①在区间(0，1)内有两相异实根，令f(x)=(a²+b²)x²－2a²x+a²(1－b²),则有

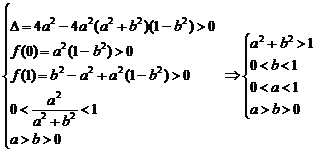
同时满足上述四个条件的点P(a,b)的存在区域为下图所示的阴影部分：

歼灭难点训练

一、1.解析：由题意知A(1，1)，B(m,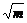),C(4,2).

直线AC所在方程为x－3y+2=0,

点B到该直线的距离为d=.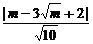

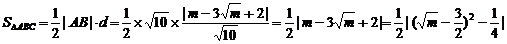
∵m∈(1,4),∴当时，S_△ABC有最大值，此时m=.

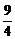答案：B

2.解析：考虑式子的几何意义，转化为求圆x²+y²=2上的点与双曲线xy=9上的点的距离的最小值.

答案：C

二、3.解析：设椭圆方程为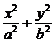=1(a＞b＞0),以OA为直径的圆：x²－ax+y²=0,两式联立消y得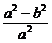x²－ax+b²=0.即e²x²－ax+b²=0,该方程有一解x₂,一解为a,由韦达定理x₂=－a,0＜x₂＜a，即0＜－a＜a＜e＜1.

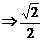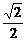答案：＜e＜1

4.解析：由题意可设抛物线方程为x²=－ay,当x=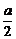时，y=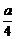－；当x=0.8时，y=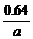－.由题意知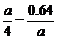≥3,即a²－12a－2.56≥0.解得a的最小整数为13.

答案：13

5.解析：设P(t,t²－1)，Q(s,s²－1)

∵BP⊥PQ,∴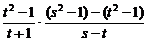=－1,

即t²+(s－1)t－s+1=0

∵t∈R,∴必须有Δ=(s－1)²+4(s－1)≥0.即s²+2s－3≥0,

解得s≤－3或s≥1.

答案：(－∞,－3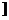∪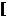1,+∞)

三、6.解：设A(x₁,y₁),B(x₂,y₂).

由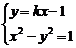,得(1－k²)x²+2kx－2=0,

又∵直线AB与双曲线左支交于A、B两点，

故有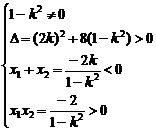

解得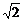－＜k＜－1

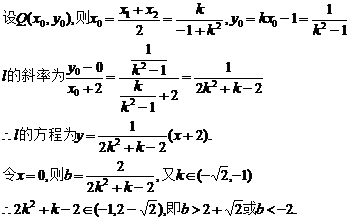
7.解：由抛物线y²=4x,得焦点F(1,0),准线l：x=－1.

(1)设P(x,y)，则B(2x－1,2y),椭圆中心O′,则|FO′|∶|BF|=e,又设点B到l的距离为d,则|BF|∶d=e,∴|FO′|∶|BF|=|BF|∶d,即(2x－2)²+(2y)²=2x(2x－2),化简得P点轨迹方程为y²=x－1(x＞1).

(2)设Q(x,y),则|MQ|=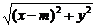　

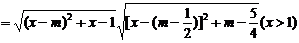
(ⅰ)当m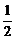－≤1,即m≤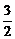时，函数t=[x－(m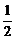－)²]+m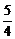－在(1，+∞)上递增，故t无最小值，亦即|MQ|无最小值.

(ⅱ)当m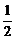－＞1,即m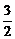＞时，函数t=[x²－(m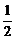－)²]+m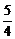－在x=m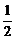－处有最小值m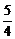－,∴|MQ|_min=.

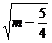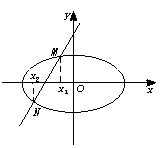
8.解：(1)以AB、OD所在直线分别为x轴、y轴，O为原点，建立平面直角坐标系，

∵|PA|+|PB|=|QA|+|QB|=2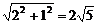＞|AB|=4.

∴曲线C为以原点为中心，A、B为焦点的椭圆.

设其长半轴为a,短半轴为b,半焦距为c,则2a=2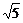,∴a=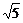,c=2,b=1.

∴曲线C的方程为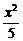+y²=1.

(2)设直线l的方程为y=kx+2,

代入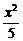+y²=1,得(1+5k²)x²+20kx+15=0.

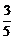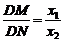Δ=(20k)²－4×15(1+5k²)＞0,得k²＞.由图可知=λ

由韦达定理得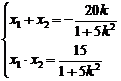

将x₁=λx₂代入得

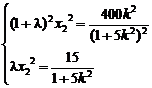
两式相除得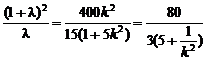

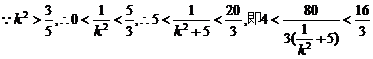
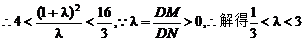　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

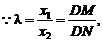M在D、N中间，∴λ＜1　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

又∵当k不存在时，显然λ=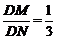　(此时直线l与y轴重合).