
网址:http://www.1010jiajiao.com/paper/timu/5160259.html[举报]
1.()已知函数f(x)=loga[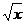 –(2a)2]对任意x∈[
–(2a)2]对任意x∈[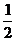 ,+∞]都有意义,则实数a的取值范围是( )
,+∞]都有意义,则实数a的取值范围是( )
A.(0,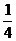
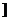 B.(0,
B.(0,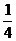 )
C.[
)
C.[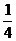 ,1
,1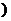 D.(
D.(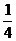 ,
,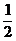 )
)
参 考 答 案
●难点磁场
1.解析:设t=3x,则t∈[1,3],原不等式可化为a2–a–3>–2t2+t,t∈[1,3].
等价于a2–a–3大于f(t)=–2t2+t在[1,3]上的最大值.
答案:(–∞,–1)∪(2,+∞)
2.解:(1)当a=1,b=–2时,f(x)=x2–x–3,由题意可知x=x2–x–3,得x1=–1,x2=3.
故当a=1,b=–2时,f(x)的两个不动点为–1,3.
(2)∵f(x)=ax2+(b+1)x+(b–1)(a≠0)恒有两个不动点,
∴x=ax2+(b+1)x+(b–1),即ax2+bx+(b–1)=0恒有两相异实根
∴Δ=b2–4ab+4a>0(b∈R)恒成立.
于是Δ′=(4a)2–16a<0解得0<a<1
故当b∈R,f(x)恒有两个相异的不动点时,0<a<1.
(3)由题意A、B两点应在直线y=x上,设A(x1,x1),B(x2,x2)
又∵A、B关于y=kx+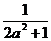 对称.
对称.
∴k=–1.设AB的中点为M(x′,y′)
∵x1,x2是方程ax2+bx+(b–1)=0的两个根.
∴x′=y′=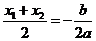 ,又点M在直线
,又点M在直线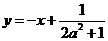 上有
上有
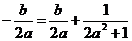 ,即
,即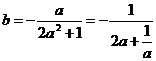
∵a>0,∴2a+ ≥2
≥2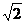 当且仅当2a=
当且仅当2a= 即a=
即a=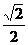 ∈(0,1)时取等号,
∈(0,1)时取等号,
故b≥–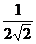 ,得b的最小值–
,得b的最小值–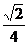 .
.
●歼灭难点训练
一、1.解析:考查函数y1=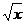 和y2=(2a)x的图象,显然有0<2a<1.由题意
和y2=(2a)x的图象,显然有0<2a<1.由题意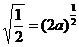 得a=
得a=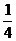 ,再结合指数函数图象性质可得答案.
,再结合指数函数图象性质可得答案.
答案:A
2.解析:由题意可得f(–x+1)=–f(x+1).令t=–x+1,则x=1–t,故f(t)=–f(2–t),即f(x)=–f(2–x).
当x>1,2–x<1,于是有f(x)=–f(2–x)=–2(x–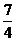 )2–
)2–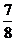 ,其递减区间为[
,其递减区间为[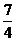 ,+∞).
,+∞).
答案:C
3.解析:显然有x>3,原方程可化为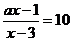
故有(10–a).x=29,必有10–a>0得a<10
又x= >3可得a>
>3可得a> .
.
答案: <a<10
<a<10
4.解析:原式化为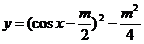 .
.
当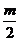 <–1,ymin=1+m=–4
<–1,ymin=1+m=–4 m=–5.
m=–5.
当–1≤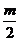 ≤1,ymin=
≤1,ymin=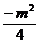 =–4
=–4 m=±4不符.
m=±4不符.
当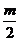 >1,ymin=1–m=–4
>1,ymin=1–m=–4 m=5.
m=5.
答案:±5
二、5.解:(1)令2x=t(t>0),设f(t)=t2–4t+a.
由f(t)=0在(0,+∞)有且仅有一根或两相等实根,则有
①f(t)=0有两等根时,Δ=0 16–4a=0
16–4a=0 a=4
a=4
验证:t2–4t+4=0 t=2∈(0,+∞),这时x=1
t=2∈(0,+∞),这时x=1
②f(t)=0有一正根和一负根时,f(0)<0 a<0
a<0
③若f(0)=0,则a=0,此时4x–4.2x=0 2x=0(舍去),或2x=4,∴x=2,即A中只有一个元素
2x=0(舍去),或2x=4,∴x=2,即A中只有一个元素
综上所述,a≤0或a=4,即B={a|a≤0或a=4}
(2)要使原不等式对任意a∈(–∞,0]∪{4}恒成立.即g(a)=(x–2)a–(x2–6x)>0恒成立.只须
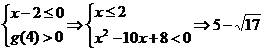 <x≤2
<x≤2
6.解:(1)∵方程ax2+bx=2x有等根,∴Δ=(b–2)2=0,得b=2.
由f(x–1)=f(3–x)知此函数图象的对称轴方程为x=–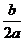 =1得a=–1,故f(x)=–x2+2x.
=1得a=–1,故f(x)=–x2+2x.
(2)f(x)=–(x–1)2+1≤1,∴4n≤1,即n≤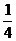
而抛物线y=–x2+2x的对称轴为x=1
∴n≤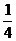 时,f(x)在[m,n]上为增函数.
时,f(x)在[m,n]上为增函数.
若满足题设条件的m,n存在,则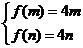

又m<n≤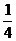 ,∴m=–2,n=0,这时定义域为[–2,0],值域为[–8,0].
,∴m=–2,n=0,这时定义域为[–2,0],值域为[–8,0].
由以上知满足条件的m、n存在,m=–2,n=0.
7.(1)证明:当n=1时,g1(x0)=x0显然成立;
设n=k时,有gk(x0)=x0(k∈N)成立,
则gk+1(x0)=f[gk(x0)]=f(x0)=g1(x0)=x0
即n=k+1时,命题成立.
∴对一切n∈N,若g1(x0)=x0,则gn(x0)=x0.
(2)解:由(1)知,稳定不动点x0只需满足f(x0)=x0
由f(x0)=x0,得6x0–6x02=x0,∴x0=0或x0=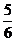
∴稳定不动点为0和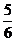 .
.
(3)解:∵f(x)<0,得6x–6x2<0 x<0或x>1.
x<0或x>1.
∴gn(x)<0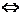 f[gn–1(x)]<0
f[gn–1(x)]<0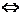 gn–1(x)<0或gn–1(x)>1
gn–1(x)<0或gn–1(x)>1
要使一切n∈N,n≥2,都有gn(x)<0,必须有g1(x)<0或g1(x)>1.
由g1(x)<0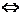 6x–6x2<0
6x–6x2<0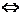 x<0或x>1
x<0或x>1
由g1(x)>0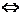 6x–6x2>1
6x–6x2>1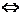
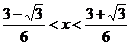
故对于区间(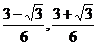 )和(1,+∞)内的任意实数x,只要n≥2,n∈N,都有gn(x)<0.
)和(1,+∞)内的任意实数x,只要n≥2,n∈N,都有gn(x)<0.
8.(1)证明:任取x1>x2>0,f(x1)–f(x2)=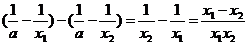
∵x1>x2>0,∴x1x2>0,x1–x2>0,
∴f(x1)–f(x2)>0,即f(x1)>f(x2),故f(x)在(0,+∞)上是增函数.
(2)解:∵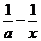 ≤2x在(0,+∞)上恒成立,且a>0,
≤2x在(0,+∞)上恒成立,且a>0,
∴a≥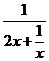 在(0,+∞)上恒成立,令
在(0,+∞)上恒成立,令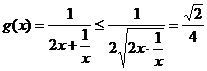 (当且仅当2x=
(当且仅当2x= 即x=
即x=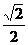 时取等号),要使a≥
时取等号),要使a≥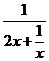 在(0,+∞)上恒成立,则a≥
在(0,+∞)上恒成立,则a≥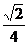 .故a的取值范
.故a的取值范
围是[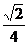 ,+∞).
,+∞).
(3)解:由(1)f(x)在定义域上是增函数.
∴m=f(m),n=f(n),即m2– m+1=0,n2–
m+1=0,n2– n+1=0
n+1=0
故方程x2– x+1=0有两个不相等的正根m,n,注意到m.n=1,故只需要Δ=(
x+1=0有两个不相等的正根m,n,注意到m.n=1,故只需要Δ=( )2–4>0,由于a>0,则0<a<
)2–4>0,由于a>0,则0<a<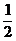 .
.