
网址:http://www.1010jiajiao.com/paper/timu/5160286.html[举报]
(人教版第121页 例1)
题目意图:用平面向量的方法证明平面几何命题:平行四边形两条对角线的平方和等于其两条邻边的平方和的两倍
变式1:如图,矩形ABCD内接于半径为r的圆O,点P是圆周上任意一点,
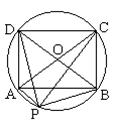 求证:PA2+PB2+PC2+PD2=8r2.
求证:PA2+PB2+PC2+PD2=8r2.
证明: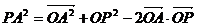 ,
,
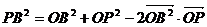 ,
,
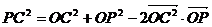 ,
,
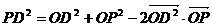 ,
,
以上各式相加可证.
变式2:已知△ABC中, ,若
,若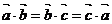 ,求证:△ABC为正三角形.
,求证:△ABC为正三角形.
证明: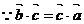 , ∴
, ∴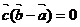 , 又∵
, 又∵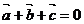 ,
, 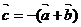 ,
,
故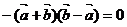 , 知a=b,
同理可知b=c , 故a=b=c , 得证.
, 知a=b,
同理可知b=c , 故a=b=c , 得证.
变式3:已知平行四边形ABCD的两条对角线AC与BD交于E,O是任意一点,求证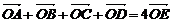 .
.
[证明]
∵E是对角线AC与BD的交点,∴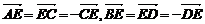 .
.
在△OAC中,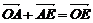 ,
,
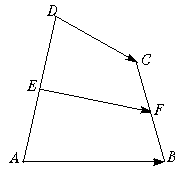
同理有 .
.
四式相加可得: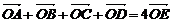 .
.
变式4:四边形ABCD的边AD和BC的中点分别为E、F,
求证: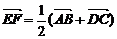
[证法一] ∵E、F分别为DA、BC的中点.
∴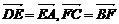
又∵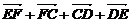 =0①
=0①
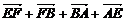 =0②
=0②
①+②,得2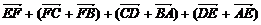 =0
=0
∴2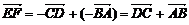
∴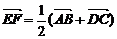
[证法二] 连结EC,EB
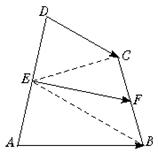
∵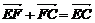 ,①
,①
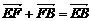 ②
②
①+②,得2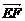 +0=
+0=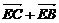 ,
,
∴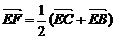
又∵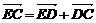 ③
③
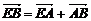 ④
④
③+④,得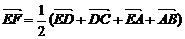
又∵ =0,
=0,
∴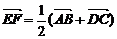 .
.