
网址:http://www.1010jiajiao.com/paper/timu/5160297.html[举报]
3.()函数f(x)=loga(3x2+5x-2)(a>0且a≠1)的单调区间_________.
参考答案
难点磁场
解:(1)由题意得f[f(x)]=f(x2+c)=(x2+c)2+c
f(x2+1)=(x2+1)2+c,∵f[f(x)]=f(x2+1)
∴(x2+c)2+c=(x2+1)2+c,
∴x2+c=x2+1,∴c=1
∴f(x)=x2+1,g(x)=f[f(x)]=f(x2+1)=(x2+1)2+1
(2)φ(x)=g(x)-λf(x)=x4+(2-λ)x2+(2-λ)
若满足条件的λ存在,则φ′(x)=4x3+2(2-λ)x
∵函数φ(x)在(-∞,-1)上是减函数,
∴当x<-1时,φ′(x)<0
即4x3+2(2-λ)x<0对于x∈(-∞,-1)恒成立
∴2(2-λ)>-4x2,
∵x<-1,∴-4x2<-4
∴2(2-λ)≥-4,解得λ≤4
又函数φ(x)在(-1,0)上是增函数
∴当-1<x<0时,φ′(x)>0
即4x2+2(2-λ)x>0对于x∈(-1,0)恒成立
∴2(2-λ)<-4x2,
∵-1<x<0,∴-4<4x2<0
∴2(2-λ)≤-4,解得λ≥4
故当λ=4时,φ(x)在(-∞,-1)上是减函数,在(-1,0)上是增函数,即满足条件的λ存在.
歼灭难点训练
一、1.解析:由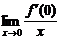 =-1,故存在含有0的区间(a,b)使当x∈(a,b),x≠0时
=-1,故存在含有0的区间(a,b)使当x∈(a,b),x≠0时 <0,于是当x∈(a,0)时f′(0)>0,当x∈(0,b)时,f′(0)<0,这样f(x)在(a,0)上单增,在(0,b)上单减.
<0,于是当x∈(a,0)时f′(0)>0,当x∈(0,b)时,f′(0)<0,这样f(x)在(a,0)上单增,在(0,b)上单减.
答案:B
2.解析:∵f′n(x)=2xn2(1-x)n-n3x2(1-x)n-1=n2x(1-x)n-1[2(1-x)-nx],令f′n(x)=0,得x1=0,x2=1,x3=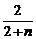 ,易知fn(x)在x=
,易知fn(x)在x=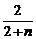 时取得最大值,最大值fn(
时取得最大值,最大值fn(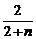 )=n2(
)=n2(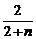 )2(1-
)2(1-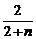 )n=4.(
)n=4.(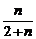 )n+1
)n+1
答案:D
二、3.解析:函数的定义域是x>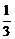 或x<-2,f′(x)=
或x<-2,f′(x)=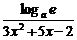 .(3x2+5x-2)′=
.(3x2+5x-2)′= ,
,
①若a>1,则当x>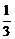 时,logae>0,6x+5>0,(3x-1)(x+2)>0,∴f′(x)>0,∴函数f(x)在(
时,logae>0,6x+5>0,(3x-1)(x+2)>0,∴f′(x)>0,∴函数f(x)在(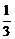 ,
,
+∞)上是增函数,x<-2时,f′(x)<0.∴函数f(x)在(-∞,-2)上是减函数.
②若0<a<1,则当x>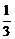 时,f′(x)<0,∴f(x)在(
时,f′(x)<0,∴f(x)在(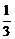 ,+∞)上是减函数,当x<-2时,f′(x)>0,∴f(x)在(-∞,-2)上是增函数
,+∞)上是减函数,当x<-2时,f′(x)>0,∴f(x)在(-∞,-2)上是增函数
答案:(-∞,-2)
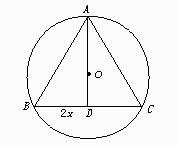 4.解析:设圆内接等腰三角形的底边长为2x,高为h,那么h=AO+BO=R+
4.解析:设圆内接等腰三角形的底边长为2x,高为h,那么h=AO+BO=R+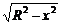 ,解得
,解得
x2=h(2R-h),于是内接三角形的面积为
S=x.h=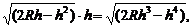
从而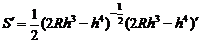
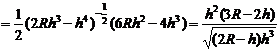
令S′=0,解得h=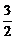 R,由于不考虑不存在的情况,所在区间(0,2R)上列表如下:
R,由于不考虑不存在的情况,所在区间(0,2R)上列表如下:
|
h |
(0,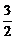 R) R) |
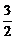 R R |
(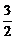 ,2R) ,2R) |
|
S′ |
+ |
0 |
- |
|
S |
增函数 |
最大值 |
减函数 |
由此表可知,当x=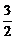 R时,等腰三角形面积最大.
R时,等腰三角形面积最大.
答案: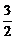 R
R
三、5.解:f′(x)=3ax2+1
若a>0,f′(x)>0对x∈(-∞,+∞)恒成立,此时f(x)只有一个单调区间,矛盾.
若a=0,f′(x)=1>0,∴x∈(-∞,+∞),f(x)也只有一个单调区间,矛盾.
若a<0,∵f′(x)=3a(x+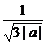 ).(x-
).(x-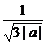 ),此时f(x)恰有三个单调区间.
),此时f(x)恰有三个单调区间.
∴a<0且单调减区间为(-∞,-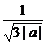 )和(
)和(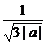 ,+∞),单调增区间为(-
,+∞),单调增区间为(-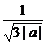 ,
, 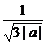 ).
).
6.解:f′(x)=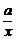 +2bx+1
+2bx+1
(1)由极值点的必要条件可知:f′(1)=f′(2)=0,即a+2b+1=0,且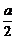 +4b+1=0,解方程组可得a=-
+4b+1=0,解方程组可得a=-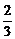 ,b=-
,b=-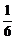 ,∴f(x)=-
,∴f(x)=-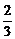 lnx-
lnx-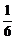 x2+x
x2+x
(2)f′(x)=-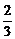 x-1-
x-1-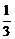 x+1,当x∈(0,1)时,f′(x)<0,当x∈(1,2)时,f′(x)>0,当x∈(2,+∞)时,f′(x)<0,故在x=1处函数f(x)取得极小值
x+1,当x∈(0,1)时,f′(x)<0,当x∈(1,2)时,f′(x)>0,当x∈(2,+∞)时,f′(x)<0,故在x=1处函数f(x)取得极小值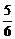 ,在x=2处函数取得极大值
,在x=2处函数取得极大值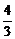 -
-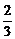 ln2.
ln2.
7.证法一:∵b>a>e,∴要证ab>ba,只要证blna>alnb,设f(b)=blna-alnb(b>e),则
f′(b)=lna-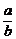 .∵b>a>e,∴lna>1,且
.∵b>a>e,∴lna>1,且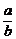 <1,∴f′(b)>0.∴函数f(b)=blna-alnb在(e,+∞)上是增函数,∴f(b)>f(a)=alna-alna=0,即blna-alnb>0,∴blna>alnb,∴ab>ba.
<1,∴f′(b)>0.∴函数f(b)=blna-alnb在(e,+∞)上是增函数,∴f(b)>f(a)=alna-alna=0,即blna-alnb>0,∴blna>alnb,∴ab>ba.
证法二:要证ab>ba,只要证blna>alnb(e<a<b ,即证
,即证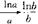 ,设f(x)=
,设f(x)=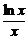 (x>e),则f′(x)=
(x>e),则f′(x)=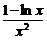 <0,∴函数f(x)在(e,+∞)上是减函数,又∵e<a<b,
<0,∴函数f(x)在(e,+∞)上是减函数,又∵e<a<b,
∴f(a)>f(b),即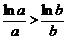 ,∴ab>ba.
,∴ab>ba.
8.解:(1)f(α)=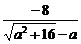 ,f(β)=
,f(β)= 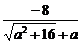 ,f(α)=f(β)=4
,f(α)=f(β)=4
(2)设φ(x)=2x2-ax-2,则当α<x<β时,φ(x)<0,
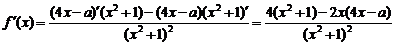
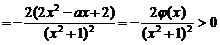
∴函数f(x)在(α,β)上是增函数
(3)函数f(x)在[α,β]上最大值f(β)>0,最小值f(α)<0,
∵|f(α).f(β)|=4,∴当且仅当f(β)=-f(α)=2时,f(β)-f(α)=|f(β)|+|f(α)|取最小值4,此时a=0,f(β)=2