
网址:http://www.1010jiajiao.com/paper/timu/5160352.html[举报]
7.()定义在(-∞,4]上的减函数f(x)满足f(m-sinx)≤f(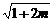 -
-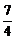 +cos2x)对任意x∈R都成立,求实数m的取值范围.
+cos2x)对任意x∈R都成立,求实数m的取值范围.
参考答案
难点磁场
解:∵f(2)=0,∴原不等式可化为f[log2(x2+5x+4)]≥f(2).
又∵f(x)为偶函数,且f(x)在(0,+∞)上为增函数,
∴f(x)在(-∞,0)上为减函数且f(-2)=f(2)=0
∴不等式可化为log2(x2+5x+4)≥2 ①
或log2(x2+5x+4)≤-2 ②
由①得x2+5x+4≥4
∴x≤-5或x≥0 ③
由②得0<x2+5x+4≤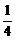 得
得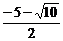 ≤x<-4或-1<x≤
≤x<-4或-1<x≤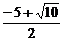 ④
④
由③④得原不等式的解集为
{x|x≤-5或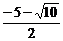 ≤x≤-4或-1<x≤
≤x≤-4或-1<x≤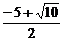 或x≥0}
或x≥0}
歼灭难点训练
一、1.解析:f(7.5)=f(5.5+2)=-f(5.5)=-f(3.5+2)=f(3.5)=f(1.5+2)=-f(1.5)=-f(-0.5+2)=
f(-0.5)=-f(0.5)=-0.5.
答案:B
2.解析:∵f(x)是定义在(-1,1)上的奇函数又是减函数,且f(a-3)+f(9-a2)<0.
∴f(a-3)<f(a2-9).
∴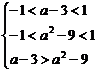 ∴a∈(2
∴a∈(2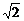 ,3).
,3).
答案:A
二、3.解析:由题意可知:xf(x)<0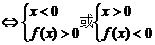
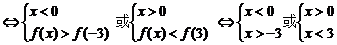
∴x∈(-3,0)∪(0,3)
答案:(-3,0)∪(0,3)
4.解析:∵f(x)为R上的奇函数
∴f(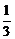 )=-f(-
)=-f(-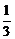 ),f(
),f(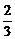 )=-f(-
)=-f(-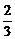 ),f(1)=-f(-1),又f(x)在(-1,0)上是增函数且-
),f(1)=-f(-1),又f(x)在(-1,0)上是增函数且-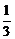 >
>
-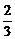 >-1.
>-1.
∴f(-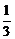 )>f(-
)>f(-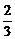 )>f(-1),∴f(
)>f(-1),∴f(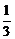 )<f(
)<f(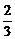 )<f(1).
)<f(1).
答案:f(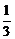 )<f(
)<f(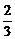 )<f(1)
)<f(1)
三、5.解:函数f(x)在(-∞,0)上是增函数,设x1<x2<0,因为f(x)是偶函数,所以
f(-x1)=f(x1),f(-x2)=f(x2),由假设可知-x1>-x2>0,又已知f(x)在(0,+∞)上是减函数,于是有f(-x1)<f(-x2),即f(x1)<f(x2),由此可知,函数f(x)在(-∞,0)上是增函数.
6.解:(1)a=1.
(2)f(x)=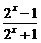 (x∈R)
(x∈R)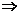 f--1(x)=log2
f--1(x)=log2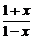 (-1<x<1
(-1<x<1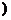 .
.
(3)由log2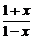 >log2
>log2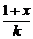
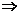 log2(1-x)<log2k,∴当0<k<2时,不等式解集为{x|1-k<x<1
log2(1-x)<log2k,∴当0<k<2时,不等式解集为{x|1-k<x<1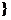 ;当k≥2时,不等式解集为{x|-1<x<1
;当k≥2时,不等式解集为{x|-1<x<1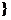 .
.
7.解: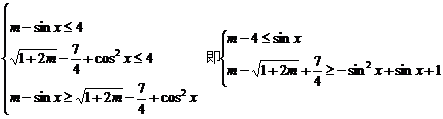 ,对x∈R恒成立,
,对x∈R恒成立,
 ∴m∈[
∴m∈[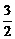 ,3]∪{
,3]∪{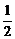 }.
}.
8.解:(1)∵f(x)是奇函数,∴f(-x)=-f(x),即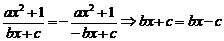
∴c=0,∵a>0,b>0,x>0,∴f(x)=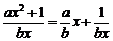 ≥2
≥2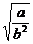 ,当且仅当x=
,当且仅当x=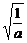 时等号成立,于是2
时等号成立,于是2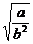 =2,∴a=b2,由f(1)<
=2,∴a=b2,由f(1)<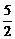 得
得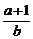 <
<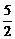 即
即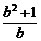 <
<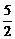 ,∴2b2-5b+2<0,解得
,∴2b2-5b+2<0,解得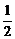 <b<2,又b∈N,∴b=1,∴a=1,∴f(x)=x+
<b<2,又b∈N,∴b=1,∴a=1,∴f(x)=x+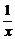 .
.
(2)设存在一点(x0,y0)在y=f(x)的图象上,并且关于(1,0)的对称点(2-x0,-y0)也在y=f(x)图象上,则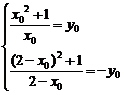
消去y0得x02-2x0-1=0,x0=1±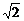 .
.
∴y=f(x)图象上存在两点(1+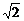 ,2
,2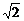 ),(1-
),(1-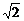 ,-2
,-2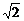 )关于(1,0)对称.
)关于(1,0)对称.