
网址:http://www.1010jiajiao.com/paper/timu/5160384.html[举报]
例1.求函数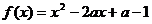 在
在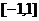 上的最小值为-2,求实数
上的最小值为-2,求实数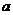 的取值 .
的取值 .
例2.已知函数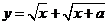 的最小值是
的最小值是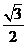 ,求实数
,求实数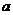 的取值 .
的取值 .
解:若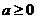 ,则函数的定义域为[0,+
,则函数的定义域为[0,+ ),且为增函数,故
),且为增函数,故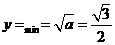 ,得
,得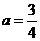 ;
;
若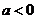 ,则函数的定义域为[-a,+
,则函数的定义域为[-a,+ ),且为增函数,故
),且为增函数,故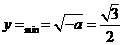 ,得
,得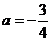 ,
,
∴ 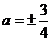 .
.
例3. (盐城市2008届高三第一次调研卷)题12
已知函数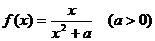 在
在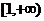 的最大值为
的最大值为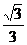 ,求实数
,求实数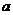 的取值 .
的取值 . 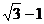
例4. (苏州市2008届高三第一次调研测试)题19
某商店经销一种奥运会纪念品,每件产品的成本为30元,并且没卖一件产品需向税务部门上交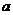 (
(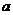 为常数,
为常数,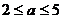 )元的税收.设每件产品的日销售价为
)元的税收.设每件产品的日销售价为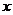
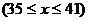 元,根据市场调查, 日销售量与
元,根据市场调查, 日销售量与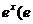 为自然对数的底数)成反比例.已知每件产品的日销售价为40元时, 日销售量为10件.
为自然对数的底数)成反比例.已知每件产品的日销售价为40元时, 日销售量为10件.
(1)
求该商店的日利润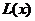 元与每件产品的日销售价
元与每件产品的日销售价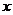 元的函数关系式;
元的函数关系式;
(2)
当没件产品的日销售价为多少时, 该商店的日利润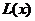 最大,并求出
最大,并求出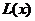 的最大值.
的最大值.
解: (1) 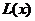 =
=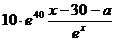
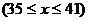 ;
;
(2) 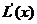 =
=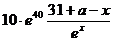
∵ 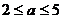 , ∴
, ∴ 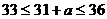
①
若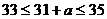 ,则
,则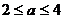 ,
, 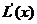
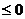 (当且仅当
(当且仅当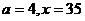 是
是
取等于号),
这时,函数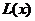 在
在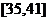 上为减函数,
上为减函数, 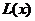 的最大值为
的最大值为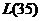 ,即10
,即10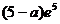 ;
;
②
若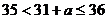 ,则
,则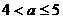 ,当
,当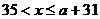 时,
时, 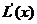
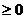 ,当
,当
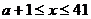 时,
时, 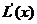
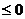 ,
,
这时, 函数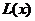 在
在 上为增函数, 在
上为增函数, 在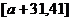 上为减函数,故函数的最大值为
上为减函数,故函数的最大值为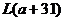 ,即
,即
∴ 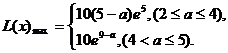
例5.求函数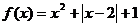 的最小值.
的最小值.
例6.设a为实数, 函数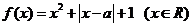 .
.
(1) 讨论函数 的奇偶性; (2) 求
的奇偶性; (2) 求 的最小值.
的最小值.
解(1): 若函数 为奇函数,
为奇函数,
则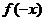 +
+ =0,即(
=0,即(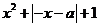 )+(
)+(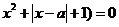 ,这是不可能的,故函数
,这是不可能的,故函数 不可能为奇函数.
不可能为奇函数.
若函数 为偶函数,
为偶函数,
则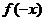 -
- =0,即(
=0,即(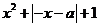 )-(
)-(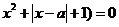 ,
,
∴ 等式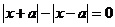 对任意
对任意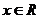 都成立, 故
都成立, 故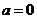 ,即
,即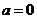 时函数
时函数 为偶函数.
为偶函数.
(2) 函数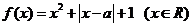 可以化为
可以化为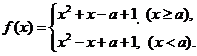
方法(一) (整体求解)
① 若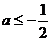 ,则函数
,则函数 在
在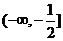 是减函数,在
是减函数,在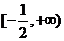 上是增函数, 故函数
上是增函数, 故函数 的最小值为
的最小值为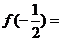
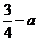 .
.
② 若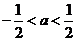 ,则函数
,则函数 在
在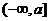 是减函数,在
是减函数,在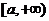 上是增函数, 故函数
上是增函数, 故函数 的最小值为
的最小值为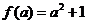 .
.
③ 若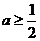 ,则函数
,则函数 在
在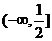 是减函数,在
是减函数,在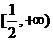 上是增函数, 故函数
上是增函数, 故函数 的最小值为
的最小值为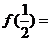
 .
.
方法(二) (分段讨论)
① 当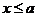 时,
时, 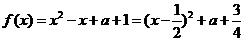 ,
,
若 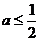 ,则函数
,则函数 在
在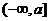 是减函数, 故函数
是减函数, 故函数 的最小值为
的最小值为
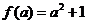 ,
,
若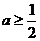 ,则函数
,则函数 的最小值为
的最小值为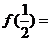
 .
.
② 当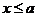 时,
时, 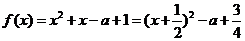 ,
,
若 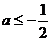 ,则函数
,则函数 的最小值为
的最小值为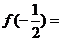
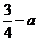 .
.
若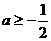 ,则函数
,则函数 在
在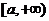 是增函数, 故函数
是增函数, 故函数 的最小值为
的最小值为
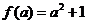 ,
,
∴ 若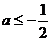 ,则函数
,则函数 的最小值为
的最小值为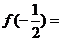
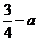 ;
;
若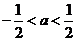 ,则函数
,则函数 的最小值为
的最小值为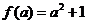 ;
;
若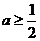 ,则函数
,则函数 的最小值为
的最小值为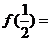
 .
.
例7.求使关于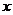 的不等式
的不等式 在
在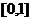 恒成立的实数
恒成立的实数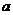 的取值范围.
的取值范围.
例8.若不等式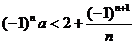 对任意的正整数
对任意的正整数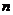 恒成立,则实数
恒成立,则实数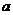 的取值范围是 .
的取值范围是 . 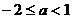
例9.已知二次函数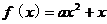 ,对于
,对于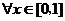 ,
,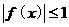 成立,试求实数
成立,试求实数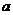 的取值范围.
的取值范围.
解: 由题设可知, 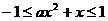 ,
,
① 若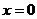 , 则
, 则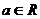 ;
;
② 若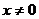 , 则
, 则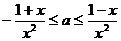 ,
,
∴ 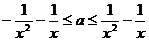 ,
, 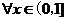 ,
,
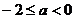 .
.
例10. (南京市2008届高三第一学期期末调研卷)题20
已知数列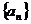 是公差为
是公差为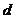 的等差数列,它的前
的等差数列,它的前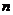 项和为
项和为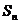 ,
,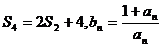 .
.
(1)
求公差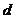 的值;
的值;
(2)
若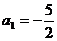 ,求数列
,求数列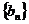 中的最大项和最小的项;
中的最大项和最小的项;
(3)
若对任意的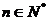 ,都有
,都有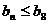 成立,求
成立,求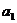 的取值范围.
的取值范围.
解:(1)∵ 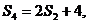 ∴
∴ 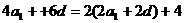 ,解得,
,解得,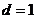 .
.
(2)
若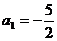 ,则
,则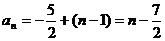 ,
,
∴ 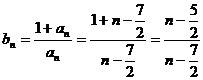 =
=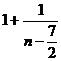
∴ 当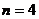 时,
时,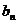 取最大值3, 当3时,
取最大值3, 当3时,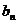 取最大值-1.
取最大值-1.
(3) 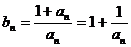 =1+
=1+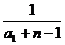 ,
,
∵ 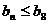 , ∴ 1+
, ∴ 1+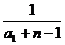
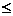 1+
1+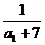 ,
, 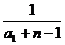
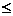
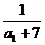 ,
,
方法①: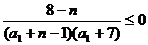
若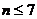 ,则
,则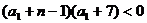 ,
,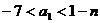 ,∴
,∴  ;
;
若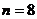 ,则
,则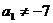
若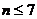 ,则
,则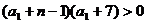 ,
, .
.
综上所述,  .
.
方法②:考虑函数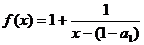
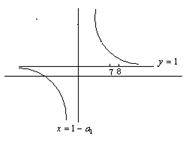
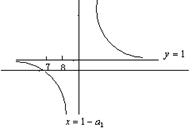
由此可知, 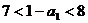 , ∴
, ∴  .
.
例11. (南京市2008届高三第一学期期末调研卷)题18
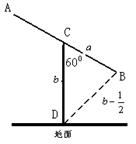 某建筑的金属支架如图所示,根据要求
某建筑的金属支架如图所示,根据要求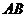 至少长2.8
至少长2.8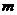 ,
,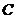 为
为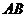 的中点,
的中点,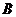 到
到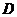 的距离比
的距离比 的长小0.5
的长小0.5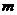 ,
,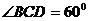 .已知金属支架每米的价格一定,问怎样设计
.已知金属支架每米的价格一定,问怎样设计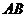 ,
, 的长, 可使建造这个支架的成本最低?
的长, 可使建造这个支架的成本最低?
解:设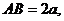
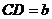 则
则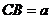 ,
,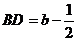
由题设可知,在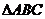 中,
中,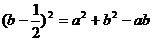 .
.
设
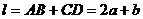 ,
,
方法①:则由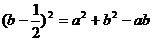 知,
知,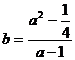 ,
,
∴ 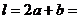
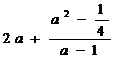
=
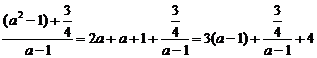
 (当且仅当
(当且仅当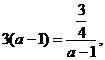 即
即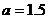 时等于号成立)
时等于号成立)
=7
这时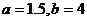 ,即
,即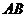 =3,
=3, =4时建造这个支架的成本最低.
=4时建造这个支架的成本最低.
方法②: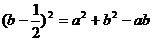 .
.
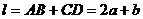 ,
,
则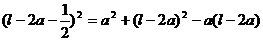 ,
,
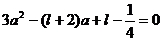
 ,
,
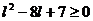 ,
, 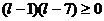 ,
,
∵  , ∴
, ∴
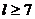 .
.
当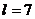 时,
时,  , 即
, 即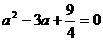 ,
,
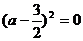 ,
, 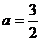 ,
,
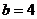 ,故7为
,故7为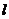 的最小值. 即
的最小值. 即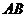 =3,
=3, =4时建造这个支架的成本最低.
=4时建造这个支架的成本最低.
方法③: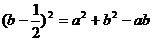 .
.
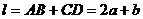 ,
,
则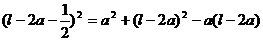 ,
,
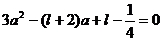
令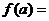
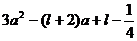 ,则函数
,则函数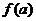 的图象与
的图象与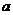 轴在
轴在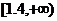 上有公共点.
上有公共点.
∴ 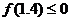 或
或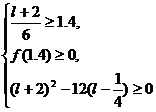 解得,
解得,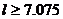 或
或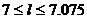 ,即
,即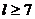 .
.
当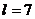 时,
时, 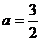 ,
,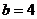 , 即
, 即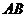 =3,
=3, =4时建造这个支架的成本最低.
=4时建造这个支架的成本最低.