
网址:http://www.1010jiajiao.com/paper/timu/5160480.html[举报]
(三)解答题
17.已知函数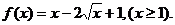
(1)求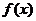 的反函数
的反函数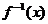 ,并指出其定义域;
,并指出其定义域;
(2)若数列{an}的前n项和Sn对所有的大于1的自然数n都有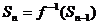 ,且a1
=1,求数列{an}的通项公式;
,且a1
=1,求数列{an}的通项公式;
(3)令
18.已知数列{an}满足
(1)求证:{an}为等比数列;
(2)记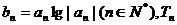 为数列{bn}的前n项和,那么:
为数列{bn}的前n项和,那么:
①当a=2时,求Tn;
②当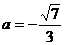 时,是否存在正整数m,使得对于任意正整数n都有
时,是否存在正整数m,使得对于任意正整数n都有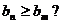 如果存在,求出m的值;如果不存在,请说明理由.
如果存在,求出m的值;如果不存在,请说明理由.
19.已知数列{an}的前n项和为Sn,且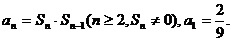
(Ⅰ)求证:数列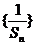 为等差数列;
为等差数列;
(Ⅱ)求满足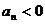 的自然数n的集合.
的自然数n的集合.
20.已知数列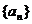 为等差数列,其前n项和为
为等差数列,其前n项和为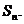
(I)若 成立,并将其整合为一个等式;
成立,并将其整合为一个等式;
(II)一般地,若存在正整数k,使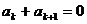 ,我们可将(I)中的结论作相应推广,试写出推广后的结论,并推断它是否正确.
,我们可将(I)中的结论作相应推广,试写出推广后的结论,并推断它是否正确.
21.已知数列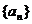 满足递推式
满足递推式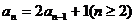 ,其中
,其中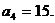
(Ⅰ)求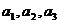 ;
;
(Ⅱ)求数列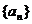 的通项公式;
的通项公式;
(Ⅲ)求数列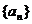 的前n项和
的前n项和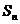 .
.
22.已知等差数列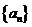 ,公差d大于0,且
,公差d大于0,且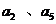 是方程
是方程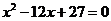 的两个根,数列
的两个根,数列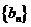 的前n项和为
的前n项和为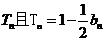 。
。
(1)求数列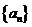 、
、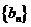 的通项公式;
的通项公式;
(2)记
强化训练题答案
1.[答案]C解析:观察出100至500之间能被11整除的数为110、121、132、…它们构成一个等差数列,公差为11,数an=110+(n-1).11=11n+99,由an≤500,解得n≤36.4,n∈N*,∴n≤36.
2.[答案]A解析:由已知:an+1=an2-1=(an+1)(an-1),
∴a2=0,a3=-1,a4=0,a5=-1.
3.[答案]D解析:a1+a4+a7,a2+a5+a8,a3+a6+a9成等差数列,故a3+a6+a9=2×39-45=33.
4.[答案]C解析:an=a1+(n-1)d,即-6+(n-1)d=0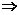 n=
n=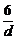 +1
+1
∵d∈N*,当d=1时,n取最大值n=7.
5.[答案]C解析:由an=-n2+10n+11=-(n+1)(n-11),得a11=0,而a10>0,a12<0,S10=S11.
6.[答案]A解析:由等差数列性质,a4+a6=a3+a7=-4与a3.a7=-12联立,即a3,a7是方程x2+4x-12=0的两根,又公差d>0,∴a7>a3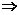 a7=2,a3=-6,从而得a1=-10,d=2,S20=180.
a7=2,a3=-6,从而得a1=-10,d=2,S20=180.
7.[答案]B
解析:f(n+1)-f(n)=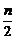
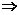
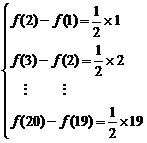
相加得f(20)-f(1)=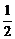 (1+2+…+19)
(1+2+…+19)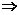 f(20)=95+f(1)=97.
f(20)=95+f(1)=97.
8.[答案]B 解析:(a2+a5)-(a1+a4)=(a2-a1)+(a5-a4)=2d.(a3+a6)-(a2+a5)=(a3-a2)+(a6-a5)=2d.依次类推.
9.[答案]D
解析: 设三边为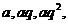 则
则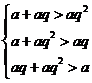 ,即
,即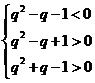
得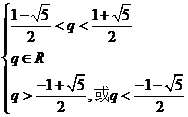 ,即
,即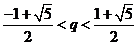
10.[答案]D
解析:1由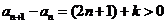 ,
,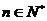 恒成立,有
恒成立,有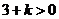 ,得
,得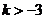 。
。
11.[答案]B
解析:
2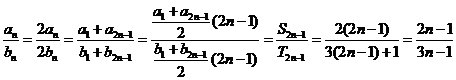 。
。
12.[答案]D解析:设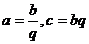 ,则有
,则有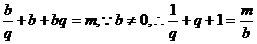 。当
。当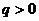 时,
时,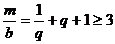 ,而
,而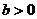 ,
,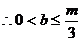 ;当
;当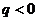 时,
时,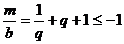 ,即
,即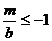 ,而
,而
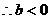 ,则
,则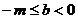 ,故
,故 。
。
13.[答案]6解析:由已知得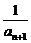 =
=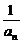 +
+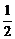 ,∴{
,∴{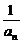 }是以
}是以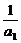 =1为首项,公差d=
=1为首项,公差d=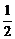 的等差数列.
的等差数列.
∴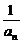 =1+(n-1)
=1+(n-1)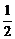 ,∴an=
,∴an=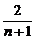 =
=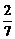 ,∴n=6.
,∴n=6.
14.[答案]-110解析:S100-S10=a11+a12+…+a100=45(a11+a100)=45(a1+a110)=-90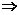 a1+a110=-2.
a1+a110=-2.
S110=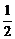 (a1+a110)×110=-110.
(a1+a110)×110=-110.
15.[答案]5解析:-21=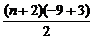 ,∴n=5.
,∴n=5.
16.[答案]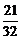 解析:
解析: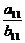 =
=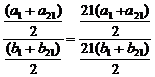 =
= .
.
17.解:(1)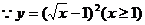
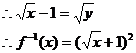
定义域为: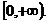
(2)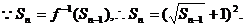
又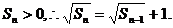
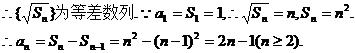
而a1
= 1符合上式,故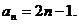
(3)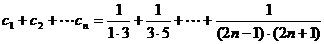
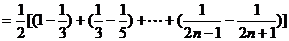
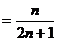
18.解:1)当n≥2时,
整理得
所以{an}是公比为a的等比数列.(4分)
(2)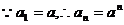
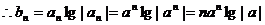
①当a=2时,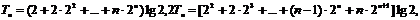
两式相减,得
 (9分)
(9分)
②因为-1<a<0,所以:当n为偶数时,
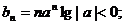
当n为奇数时,
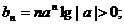
所以,如果存在满足条件的正整数m,则m一定是偶数.
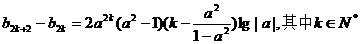
当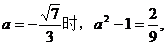
所以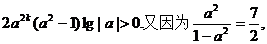
所以当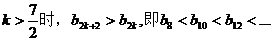
当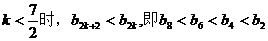
故存在正整数m=8,使得对于任意正整数n都有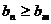
19.解:(Ⅰ)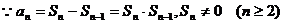

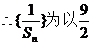 为首项,-1为公差的等差数列.
为首项,-1为公差的等差数列.
(Ⅱ)由(Ⅰ)知,
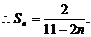
当

由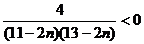 ,解得
,解得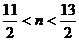 ,而
,而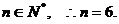
故所求n的集合为{6}.
20.解:(I)
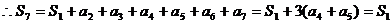 ;
;
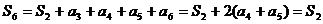 ;
;
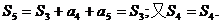
∴对任意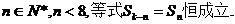
(II)推广:设等差数列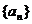 的前n项和为Sn,若存在正整数k,使
的前n项和为Sn,若存在正整数k,使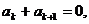
则对任意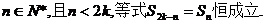
设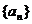 的公差为
的公差为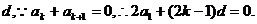
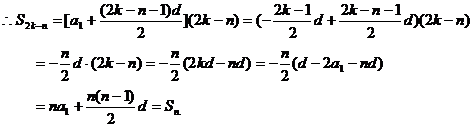
故推广后的结论正确.
21.解:(1)由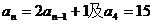 知
知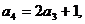
解得: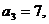 同理得
同理得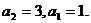
(2)由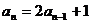 知
知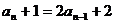
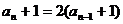
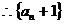 构成以
构成以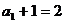 为首项以2为公比的等比数列;
为首项以2为公比的等比数列;
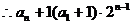 ;
;
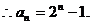 为所求通项公式
为所求通项公式
(3)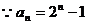
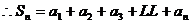
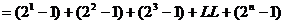

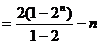

22.解:(1)设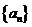 的公差为d,由题意得:
的公差为d,由题意得:
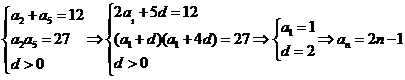
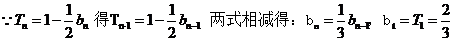

(2)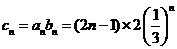
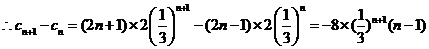
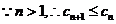
创新试题答案
1.解:(1)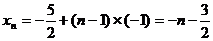
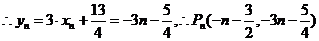
(2)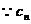 的对称轴垂直于
的对称轴垂直于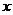 轴,且顶点为
轴,且顶点为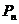 .
. 设
设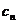 的方程为:
的方程为:
把 代入上式,得
代入上式,得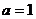 ,
,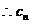 的方程为:
的方程为: 。
。
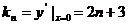 ,
,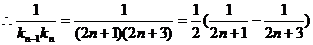

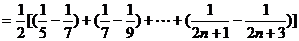
=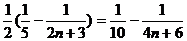
2.解 (1)由S1=a1=1,S2=1+a2,得3t(1+a2)-(2t+3)=3t
(1)由S1=a1=1,S2=1+a2,得3t(1+a2)-(2t+3)=3t ∴a2=
∴a2=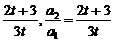

又3tSn-(2t+3)Sn-1=3t, ①
3tSn-1-(2t+3)Sn-2=3t ②
①-②得3tan-(2t+3)an-1=0 ∴
∴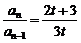 ,n=2,3,4…,
,n=2,3,4…,
所以{an}是一个首项为1公比为 的等比数列;
的等比数列;
(2)由f(t)=  =
=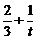 ,得bn=f(
,得bn=f(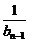 )=
)=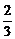 +bn-1
+bn-1
可见{bn}是一个首项为1,公差为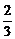 的等差数列
的等差数列 于是bn=1+
于是bn=1+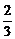 (n-1)=
(n-1)=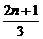 ;
;
(3)由bn=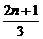 ,可知{b2n-1}和{b2n}是首项分别为1和
,可知{b2n-1}和{b2n}是首项分别为1和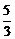 ,公差均为
,公差均为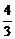 的等差数列,
的等差数列,
于是b2n=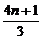 ,
,
∴b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1
=b2(b1-b3)+b4(b3-b5)+…+b2n(b2n-1-b2n+1)
=-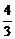 (b2+b4+…+b2n)=-
(b2+b4+…+b2n)=-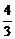 .
.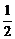 n(
n(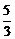 +
+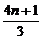 )=-
)=-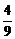 (2n2+3n)
(2n2+3n)
四、复习建议
1.“巧用性质、减少运算量”在等差、等比数列的计算中非常重要,但用“基本量法”并树立“目标意识”,“需要什么,就求什么”,既要充分合理地运用条件,又要时刻注意题的目标,往往能取得与“巧用性质”解题相同的效果
2.归纳--猜想--证明体现由具体到抽象,由特殊到一般,由有限到无限的辩证思想.学习这部分知识,对培养学生的逻辑思维能力,计算能力,熟悉归纳、演绎的论证方法,提高分析、综合、抽象、概括等思维能力,都有重大意义.
3.解答数列与函数的综合问题要善于综合运用函数方程思想、化归转化思想等数学思想以及特例分析法,一般递推法,数列求和及求通项等方法来分析、解决问题.
4.数列与解析几何的综合问题解决的策略往往是把综合问题分解成几部分,先利用解析几何的知识以及数形结合得到数列的通项公式,然后再利用数列知识和方法求解.