
网址:http://www.1010jiajiao.com/paper/timu/5160565.html[举报]
5. 函数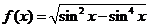 的最小正周期是
的最小正周期是
A 2π B π C 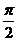 D
D 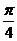
6 若集合A=
若集合A=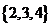 ,B=
,B=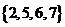 ,从这两个集合中各取一个元素作为平面直角坐标系中点的坐标,能够确定的不同点的个数为
,从这两个集合中各取一个元素作为平面直角坐标系中点的坐标,能够确定的不同点的个数为
A 11 B 12 C 23 D 24
7 已知x
已知x y满足约束条件
y满足约束条件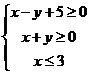 ,则
,则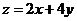 的最小值是
的最小值是
A 5 B -6 C 10 D -10
8 若0<a<1
若0<a<1 0<b<1,且
0<b<1,且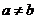 ,则下列各式中值最大的是
,则下列各式中值最大的是
 A
A 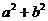 B
B 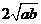 C
C 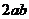 D
D 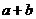
9 已知E
已知E F分别是正方形ABCD的边AB和CD中的中点,沿EF把正方形拆成一个直二面角(如图),则异面直线BF
F分别是正方形ABCD的边AB和CD中的中点,沿EF把正方形拆成一个直二面角(如图),则异面直线BF ED所成角的余弦值为
ED所成角的余弦值为
A 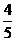 B
B 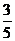 C
C 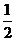 D
D 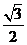
 10
10 某港口水深度y是时间t的函数(0≤t≤24,单位:小时)的函数,记作y=f(t),其曲线可以近似的看成函数y=Asinωt+b的图象(如图),一般情况下船舶航行是,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只须不碰海底即可),某船的吃水深度(船底离水面的距离)为6
某港口水深度y是时间t的函数(0≤t≤24,单位:小时)的函数,记作y=f(t),其曲线可以近似的看成函数y=Asinωt+b的图象(如图),一般情况下船舶航行是,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只须不碰海底即可),某船的吃水深度(船底离水面的距离)为6 5m,如果该船必须在同一天内(24小时)安全进出港,则它能在港口内停留最长的时间为(进出港所需时间忽略不计)
5m,如果该船必须在同一天内(24小时)安全进出港,则它能在港口内停留最长的时间为(进出港所需时间忽略不计)
A 14小时 B 15小时
C 16小时 D 17小时
高中数学综合训练系列试题(23)
参考答案及评分标准
一、选择题 BDBCC CBDAC
二、填空题 11
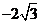 ;12
;12 8;13
8;13
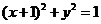 (3分),0≤m≤2(2分);
14
(3分),0≤m≤2(2分);
14 ②④
②④
三、解答题
15 设等差数列的首项为
设等差数列的首项为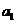
 公差为d,由已知条件可列方程
公差为d,由已知条件可列方程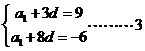 分,
分,
解得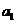 =18,d=-3
=18,d=-3 7分
7分
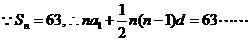 9分
9分
即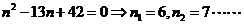 12分
12分
 满足条件的n值分别是6和7
满足条件的n值分别是6和7
 13分
13分
16 解:(1)这位司机在第i,i+1(1
解:(1)这位司机在第i,i+1(1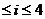 )个交通岗未遇到红灯,在第i+2个交通岗遇到红灯,所以
)个交通岗未遇到红灯,在第i+2个交通岗遇到红灯,所以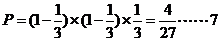 分
分
(2)由题意可知,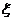 -
-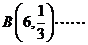 9分
9分 所以
所以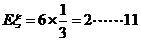 分,
分,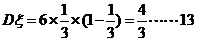 分
分
17 (1)证明:在正方形ABCD中,BC∥AD,且BC
(1)证明:在正方形ABCD中,BC∥AD,且BC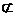 面PAD,所以BC∥D面PAD………2分
面PAD,所以BC∥D面PAD………2分
面PAD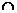 面ABCD=EF,所以BC∥EF………4分 又因为BC∥AD,所以EF∥AD………5分
面ABCD=EF,所以BC∥EF………4分 又因为BC∥AD,所以EF∥AD………5分
(2)解:取AB中点O,CD中点G,C O为原点,AB OG
OG OP所在直线为x轴
OP所在直线为x轴 y轴
y轴 z轴建立空间直角坐标系,则A(-1,0,0),B(1,0,0),C(1,2,0),P(0,0,
z轴建立空间直角坐标系,则A(-1,0,0),B(1,0,0),C(1,2,0),P(0,0, )……7分 由(1)知EF∥AD,E为PD的中点,所以F为PA的中点,
)……7分 由(1)知EF∥AD,E为PD的中点,所以F为PA的中点,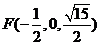 ……8分
……8分
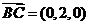 ,
,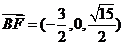 ,
,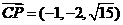 ……9分
……9分
设面BCEF的一个法向量为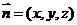 ,由
,由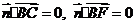 得
得
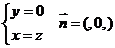 ………10分
cos<
………10分
cos<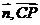 >=
>=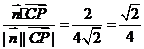 ………12分
………12分
∴直线PC与面BCEF所成的角是arcsin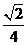 …………13分
…………13分
18 (1)解:任意
(1)解:任意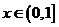 ,则
,则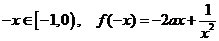 ………3分
………3分
∵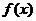 是奇函数,∴
是奇函数,∴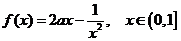 ………7分
………7分
(2)证明: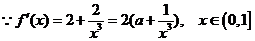 ………10分
………10分
∴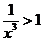 又知a>-1,∴
又知a>-1,∴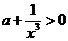 …………12分
…………12分
即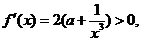 ∴
∴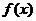 在
在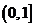 上单调递增………13分
上单调递增………13分
19 解(1)由已知条件可知:降低征税率为(10-x)﹪,农产品收购量为
解(1)由已知条件可知:降低征税率为(10-x)﹪,农产品收购量为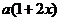 ﹪,农贸公司收购农产品总额为200
﹪,农贸公司收购农产品总额为200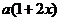 ﹪………6分
﹪………6分
∴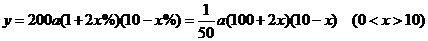 ………8分
………8分
(2)由题意知: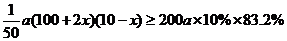 ………10分
………10分
即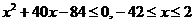 ………12分
………12分
∵0<x<10,∴0<x≤2………14分
答:略
20 解:(1)由已知可得
解:(1)由已知可得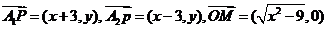 ………1分
………1分
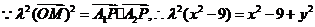
即P点的轨迹方程是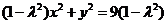 ………3分
………3分
当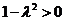 且
且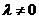 ,即
,即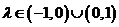 时,有
时,有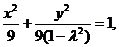 P点的轨迹是椭圆
P点的轨迹是椭圆
当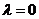 时,方程为
时,方程为 的轨迹是圆
的轨迹是圆
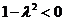 ,即
,即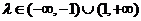 时,方程为
时,方程为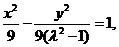 P点的轨迹是双曲线
P点的轨迹是双曲线
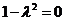 ,即
,即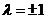 时,方程为y=0, P点的轨迹是直线
时,方程为y=0, P点的轨迹是直线 ………7分
………7分
(2)过点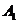 且斜率为1的直线方程为y=x+3………8分
且斜率为1的直线方程为y=x+3………8分
当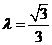 时,曲线方程为
时,曲线方程为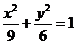
由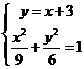 得
得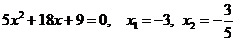 ………10分
………10分
从而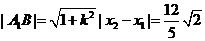 ………12分
………12分
设C(-9,y),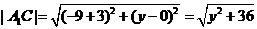
因为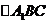 是正三角形,
是正三角形,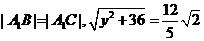 ,即
,即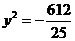 ,无解,
,无解,
所以在直线x=3上找不到点C,使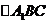 是是正三角形
是是正三角形 ………14分
………14分