
网址:http://www.1010jiajiao.com/paper/timu/5160573.html[举报]
6. 正方体的内切球与其外接球的体积之比为____________.
参考答案
一、填空题:(70分)
1.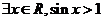 2.
2. 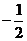 3.4
4.4 5.
3.4
4.4 5. 6.
6.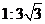 7.-1 8.
7.-1 8.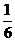 9.
9.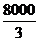 10.10 11.25
12.2550 13.
10.10 11.25
12.2550 13. 14.
14.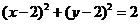
二、解答题
15.(I)在△ABC中有B+C=π-A,由条件可得:
4[1-cos(B+C)] -4cos2A+2=7
又∵cos(B+C)= -cosA
∴4cos2A-4cosA+1=0
解得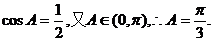
解: (II)由
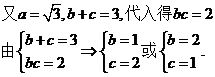
16. (Ⅰ)∵ABCD-A1B1C1D1是正四棱柱,∴CC1⊥平面ADCD, ∴BD⊥CC1
 ∵ABCD是正方形 ∴BD⊥AC
又∵AC,CC1
∵ABCD是正方形 ∴BD⊥AC
又∵AC,CC1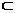 平面ACC1A1,
平面ACC1A1,
且AC∩CC1=C, ∴BD⊥平面ACC1A1.
(Ⅱ) 设BD与AC相交于O,连接C1O. ∵CC1⊥平面ADCD, ∴BD⊥AC,
∴BD⊥C1O, ∴∠C1OC∠是二面角C1-BD-C的平面角,
∴∠C1OC=60o. 连接A1B. ∵A1C1//AC, ∴∠A1C1B是BC1与AC所成的角.
设BC=a,则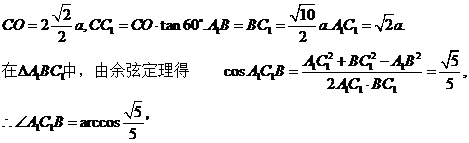 ∴异面直线BC1与AC所成角的大小为
∴异面直线BC1与AC所成角的大小为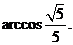
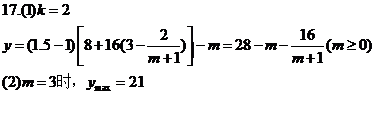
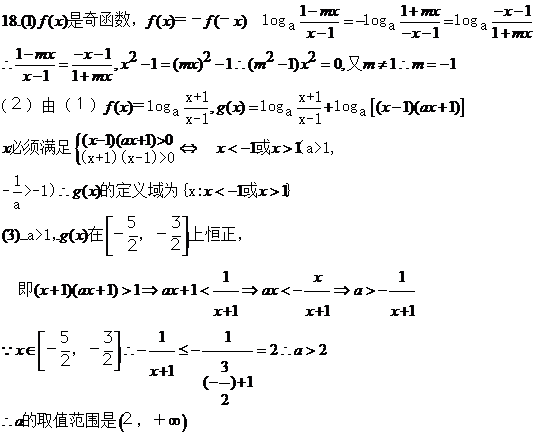
19. 解:(Ⅰ)由已知条件,得F(0,1),λ>0.
设A(x1,y1),B(x2,y2).由=λ,
即得 (-x1,1-y)=λ(x2,y2-1),
将①式两边平方并把y1=x12,y2=x22代入得 y1=λ2y2 ③
解②、③式得y1=λ,y2=,且有x1x2=-λx22=-4λy2=-4,
抛物线方程为y=x2,求导得y′=x.
所以过抛物线上A、B两点的切线方程分别是
y=x1(x-x1)+y1,y=x2(x-x2)+y2,
即y=x1x-x12,y=x2x-x22.
解出两条切线的交点M的坐标为(,)=(,-1). ……4分
所以.=(,-2).(x2-x1,y2-y1)=(x22-x12)-2(x22-x12)=0
所以.为定值,其值为0. ……7分
(Ⅱ)由(Ⅰ)知在△ABM中,FM⊥AB,因而S=|AB||FM|.
|FM|==
=
==+.
因为|AF|、|BF|分别等于A、B到抛物线准线y=-1的距离,所以
|AB|=|AF|+|BF|=y1+y2+2=λ++2=(+)2.
于是 S=|AB||FM|=(+)3,
由+≥2知S≥4,且当λ=1时,S取得最小值4.
20. (Ⅰ)由ni=1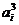 =Sn2,
(1) 由n+1i=1
=Sn2,
(1) 由n+1i=1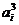 =Sn+12,
(2)
=Sn+12,
(2)
(2)-(1),得 =(Sn+1+Sn)(Sn+1-Sn)=(2 Sn+an+1) an+1.
=(Sn+1+Sn)(Sn+1-Sn)=(2 Sn+an+1) an+1.
∵ an+1 >0,∴an+12-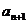 =2Sn.
=2Sn.
由an+12-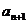 =2Sn,及an2-an =2Sn-1 (n≥2),
=2Sn,及an2-an =2Sn-1 (n≥2),
两式相减,得(an+1+ an)( an+1-an)= an+1+ an.
∵an+1+ an >0,∴an+1-an =1(n≥2)
当n=1,2时,易得a1=1,a2=2,∴an+1 - an =1(n≥1).
∴{ an}成等差数列,首项a1=1,公差d=1,故an=n .
(Ⅱ)由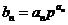 ,得
,得 。所以
。所以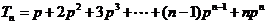 ,
,
当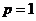 时,
时,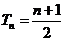 ;
;
当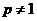 时,
时,
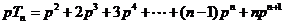 ,
,
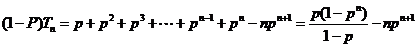
即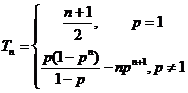
(Ⅲ)nk=1 =nk=1
=nk=1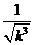 <1+nk=2
<1+nk=2
<1+nk=2=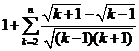
=1+ nk=2 (-)
=1+1+ -
- -<2+
-<2+ <3.
<3.