
网址:http://www.1010jiajiao.com/paper/timu/603191.html[举报]
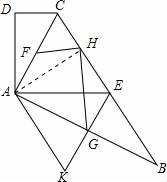
27.如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.
(1)求证:AC2=CDBC;
(2)过E作EG⊥AB,并延长EG至点K,使EK=EB.
①若点H是点D关于AC的对称点,点F为AC的中点,求证:FH⊥GH;
②若∠B=30°,求证:四边形AKEC是菱形.


[分析](1)欲证明AC2=CDBC,只需推知△ACD∽△BCA即可;
(2)①连接AH.构建直角△AHC,利用直角三角形斜边上的中线等于斜边的一半、等腰对等角以及等量代换得到:∠FHG=∠CAB=90°,即FH⊥GH;
②利用“在直角三角形中,30度角所对的直角边等于斜边的一半”、“直角三角形斜边上的中线等于斜边的一半”推知四边形AKEC的四条边都相等,则四边形AKEC是菱形.
[解答]证明:(1)∵AC平分∠BCD,
∴∠DCA=∠ACB.
又∵AC⊥AB,AD⊥AE,
∴∠DAC+∠CAE=90°,∠CAE+∠EAB=90°,
∴∠DAC=∠EAB.
又∵E是BC的中点,
∴AE=BE,
∴∠EAB=∠ABC,
∴∠DAC=∠ABC,
∴△ACD∽△BCA,
∴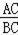
 =
=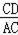
 ,
,
∴AC2=CDBC;
(2)①证明:连接AH.
∵∠ADC=∠BAC=90°,点H、D关于AC对称,
∴AH⊥BC.
∵EG⊥AB,AE=BE,
∴点G是AB的中点,
∴HG=AG,
∴∠GAH=GHA.
∵点F为AC的中点,
∴AF=FH,
∴∠HAF=∠FHA,
∴∠FHG=∠AHF+∠AHG=∠FAH+∠HAG=∠CAB=90°,
∴FH⊥GH;
②∵EK⊥AB,AC⊥AB,
∴EK∥AC,
又∵∠B=30°,
∴AC=
 BC=EB=EC.
BC=EB=EC.
又EK=EB,
∴EK=AC,
即AK=KE=EC=CA,
∴四边形AKEC是菱形.

[点评]本题考查了四边形综合题,需要熟练掌握相似三角形的判定与性质,“直角三角形斜边上的中线等于斜边的一半”、“在直角三角形中,30度角所对的直角边等于斜边的一半”以及菱形的判定才能解答该题,难度较大.