|
试题详情
7.设曲线y=和曲线y=在它们交点处的两切线的夹角为θ,则tanθ=( )
A.1
B.
C. D. 试题详情
8. 为不共线的向量,且 为不共线的向量,且 =1,以下四个向量中模最小的为( ) =1,以下四个向量中模最小的为( ) 试题详情
试题详情
9.把曲线 按向量 按向量 =(1,2)平移后得曲线C2,曲线C2有一条准线方程为x=5,则k的值为 ( ) =(1,2)平移后得曲线C2,曲线C2有一条准线方程为x=5,则k的值为 ( ) A.±3 B.3 C.±2 D.-3 试题详情
10.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( ) A.4,6,1,7 B.7,6,1,4
C.6,4,1,7 D.1,6,4,7 试题详情
11、函数 在(0,5)上是( ) 在(0,5)上是( ) A、单调增函数 B、单调减函数 试题详情
试题详情
12.椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线会经过椭圆的另一个焦点,今有一个水平放置的椭圆形台球盘,点A,B是它的两个焦点,长轴长为2a,焦距为2c,静放在点A的小球(小球的半径不计),从点A沿直线出发,经椭圆壁反弹后第一次回到点A时,小球经过的路程是
(
) A.2(a-c) B.4a C.2(a+c) D.以上答案均有可能 试题详情
二、填空题(每题4分,共16分) 13.已知f(x)是周期为2的奇函数,且当x∈(0,1)时,f(x)=2x,则f(log 7)=______________. 7)=______________. 试题详情
14.函数 的单调递减区间是________________________. 的单调递减区间是________________________. 试题详情
15.二项式( )9的展开式中第――――项是x2项,其系数为―――― )9的展开式中第――――项是x2项,其系数为―――― 试题详情
16.已知直线a和平面α、β, ,a在α、β内的射影分别为直线b和c,则b、c的位置关系可能是――――――(填写你认为正确的序号,每少写一个扣2分,扣完为止;凡填错一个得0分) ,a在α、β内的射影分别为直线b和c,则b、c的位置关系可能是――――――(填写你认为正确的序号,每少写一个扣2分,扣完为止;凡填错一个得0分) ①重合; ②相交; ③平行; ④异面 试题详情
三、解答题本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. 17.(本题满分12分)已知A(3,0),B(0,3),C(cos ,sin ,sin ). ). 试题详情
(1)若 =-1,求sin2 =-1,求sin2 的值; 的值; 试题详情
试题详情
18.
(本题满分12分) 高三(1)班的一个研究性学习小组在网上查知,某珍稀植物种子在一定条件下发芽成功的概率为 ,该研究性学习小组又分成两个小组进行验证性实验。 ,该研究性学习小组又分成两个小组进行验证性实验。 (1)第一小组做了5次这种植物种子的发芽实验(每次均种下一粒种子),求他们的实验至少有3次成功的概率; 试题详情
(2)第二小组做了若干次发芽实验(每次均种下一粒种子),如果在一次实验中种子发芽成功就停止实验,否则将继续进行下次实验,直到种子发芽成功为止,但发芽实验的次数最多不超过5次,求第二小组所做种子发芽实验的次数 的概率分布列和期望。 的概率分布列和期望。 试题详情
19.(本题满分12分)如图,P是边长为1的正六边形ABCDEF所在平面外一点, PA=1,P在平面ABC内的射影为BF的中点O。 (Ⅰ)证明PA⊥BF; (Ⅱ)求面APB与面DPB所成二面角的大小。 试题详情
试题详情
设函数 试题详情
(1)求函数 的单调区间、极值. 的单调区间、极值. 试题详情
(2)若当 时,恒有 时,恒有 ,试确定a的取值范围. ,试确定a的取值范围. 试题详情
21.(本题满分12分)已知数列 满足 满足 试题详情
(I)证明:数列 是等比数列; 是等比数列; 试题详情
(II)求数列 的通项公式; 的通项公式; 试题详情
试题详情
22.(本题满分14分) 已知双曲线C的中心在原点,焦点F1、F2在坐标轴上,一条渐近线方程为x+y=0,且过点 试题详情
(4,- ). ). (Ⅰ)求双曲线方程; 试题详情
(Ⅱ)设点M在双曲线上, =(x,y),当 =(x,y),当 ? ? ≤0,求x的取值范围.并求 ≤0,求x的取值范围.并求 ? ? =0时△F1F2M的内切圆面积.(计算结果分母可不有理化) =0时△F1F2M的内切圆面积.(计算结果分母可不有理化) 学校:栾城第二中学 姓名_______________ 准考证号码_____________分数___________ 2006-2007栾城二中第二次月考答案纸 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 试题详情
二、填空题(每题4分,共16分) 13.____________ 14._____________ 15.______________ __________________
试题详情
16._______________________________ 试题详情
三、解答题
试题详情
试题详情
 19.(本题满分12分) 19.(本题满分12分)
试题详情
试题详情
试题详情
22.(本题满分14分) 模拟卷(二)答案 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B A B C A C C A B C C D 试题详情
二、填空题 13.
-7/4
14. (1
+∞) 15. 四
;  16.②③④ 16.②③④ 试题详情
15.(1)解: , , 1分
1分 试题详情
试题详情
∴ 试题详情
∴ 4分
4分 试题详情
∴ 6分
6分 试题详情
(2)∵ 7分
7分 试题详情
∴ 8分
8分 试题详情
化简得 ,
9分 ,
9分 试题详情
∵ , ∴ , ∴ 10分
10分 试题详情
∴ = = 11分
11分 试题详情
试题详情
16.解:(I)做5次试验相当于进行了5次独立重复试验。至少有3次发芽成功,即有3次、4次、5次发芽成功,且互斥
1分 试题详情
∴所求概率 5分
5分 试题详情
(II) 可取1,2,3,4,5
6分 可取1,2,3,4,5
6分 试题详情
 =1表示第一次种子就发芽, =1表示第一次种子就发芽, ; ;
试题详情
 =2表示第一次未发芽第二次才发芽, =2表示第一次未发芽第二次才发芽,
试题详情
同理, , , 试题详情
 =5表示前四次均未发芽, =5表示前四次均未发芽, 8分
8分
试题详情
∴ 的分布列为: 的分布列为: 试题详情

1 2 3 4 5 P 试题详情
试题详情
试题详情
试题详情
试题详情

10分 试题详情
 12分 12分 试题详情
19. (本题满分12分)解:(Ⅰ)在正六边形ABCDEF中,ΔABF为等腰三角形, ∵P在平面ABC内的射影为O,∴PO⊥平面ABF,∴AO为PA在平面ABF内的射影;∵O为BF中点,∴AO⊥BF,∴PA⊥BF。 试题详情
(Ⅱ)∵PO⊥平面ABF,∴平面PBF⊥平面ABC;而O为BF中点,ABCDEF是正六边形 ,∴A、O、D共线,且直线AD⊥BF,则AD⊥平面PBF;又∵正六边形ABCDEF的边长为1,∴AO= ,AO= ,AO= ,BO= ,BO= 。 。 过O在平面POB内作OH⊥PB于H,连AH、DH,则AH⊥PB,DH⊥PB,所以∠AHD为所求二面角平面角。 试题详情
在ΔAHO中,OH= ,tan∠AHO= ,tan∠AHO= 。 。 试题详情
在ΔDHO中,tan∠DHO= ; ; 试题详情
而tan∠AHD=tan(∠AHO+∠DHO)= 试题详情
试题详情
试题详情
试题详情
20.解:(1) = = 1分
1分 试题详情
令 得 得 2分
2分 列表如下: x (-∞,a) a (a,3a) 3a (3a,+∞) 试题详情

- 0 + 0 - 试题详情
试题详情

极小 试题详情

极大 试题详情

4分 试题详情
∴ 在(a,3a)上单调递增,在(-∞,a)和(3a,+∞)上单调递减 6分 在(a,3a)上单调递增,在(-∞,a)和(3a,+∞)上单调递减 6分 试题详情
试题详情
(2) 试题详情
∵ ,∴对称轴 ,∴对称轴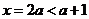 , , 试题详情
∴ 在[a+1,a+2]上单调递减
9分 在[a+1,a+2]上单调递减
9分 试题详情
∴ , , 10分 试题详情
试题详情
即 试题详情
解得 ,又 ,又 试题详情
∴a的取值范围是 14分
14分 试题详情
21.解析:本小题主要考查数列、不等式等基本知识,考查化归的数学思想方法,考查综合解题能力。满分14分。 试题详情
(I)证明: 试题详情
试题详情
试题详情
(II)解:由(I)得 试题详情
试题详情
试题详情
(III)证明: 试题详情
试题详情
 ① ①
试题详情
 ② ②
试题详情
②-①,得 试题详情
即 ③ ③ 试题详情
 ④ ④ 试题详情
④-③,得 试题详情
即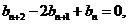 试题详情

 是等差数列。 是等差数列。
试题详情
试题详情
试题详情
解得 =2
3分 =2
3分 试题详情
∴双曲线C的方程为 - - =2
4分 =2
4分 试题详情
试题详情
 8分
8分
试题详情
试题详情
试题详情
设内切圆的圆心坐标为P(x0,y0),则 =R,由三角形面积公式得 =R,由三角形面积公式得 试题详情
试题详情
∵ =4, =4, 试题详情
 代入上式得 代入上式得
试题详情
试题详情
试题详情
| 
 ,则
,则 在复平面内对应的点位于( )
在复平面内对应的点位于( ) 是连续函数,则
是连续函数,则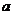 等于 ( )
等于 ( ) ,且α在第二象限,则
,且α在第二象限,则 ( )
( ) 或-3 B.
或-3 B. D.3 或-
D.3 或-
 ,④y=
,④y=
 内连续的函数的是
内连续的函数的是 ,则f(4-x2)的单调递减区间是 ( )
,则f(4-x2)的单调递减区间是 ( )
 B、
B、