|
试题详情
10、设f(x)是定义在R上以6为周期的函数,f(x)在(0,3)内单调递增,且y=f(x)的图象关于直线x=3对称,则下面正确的结论是 试题详情
A. f(6.5)<f(3.5)<f(1.5) B. f(3.5)<f(1.5)<f(6.5) 试题详情
C. f(6.5)<f(1.5)<f(3.5) D. f(3.5)<f(6.5)<f(1.5) 第Ⅱ卷 选择题(满分100分) 试题详情
二、填空题:本大题共6小题,每小题5分,共30分。把答案填写在答题卡相应位置上。 11、方程 的解集是 的解集是
试题详情
试题详情
13、若正整数m满足 试题详情
14、若函数 是奇函数,则a=
. 是奇函数,则a=
. 试题详情
试题详情
16、设f(x)是定义在R上的奇函数,且y=f (x)的图象关于直线 对称,则f (1)+ f (2)+ f (3)+ f (4)+ f
(5)=________________. 对称,则f (1)+ f (2)+ f (3)+ f (4)+ f
(5)=________________. 试题详情
三、解答题:本大题共5小题,共70分。解答应写出文字说明、证明过程或演算步骤。 17、设函数 的定义域为集合M,函数 的定义域为集合M,函数 的定义域为集合N.求: 的定义域为集合N.求: (1)集合M,N; 试题详情
(2)集合 , , . . 试题详情
18、设函数 ,且在闭区间[0,7]上,只有 ,且在闭区间[0,7]上,只有 试题详情
(Ⅰ)试判断函数 的奇偶性; 的奇偶性; 试题详情
(Ⅱ)试求方程 在闭区间[-2005,2005]上的根的个数,并证明你的结论. 在闭区间[-2005,2005]上的根的个数,并证明你的结论. 试题详情
19、设函数 . . 试题详情
(1)在区间 上画出函数 上画出函数 的图像; 的图像; 试题详情
试题详情
试题详情
试题详情
20、已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x. (Ⅰ)求函数g(x)的解析式; (Ⅱ)解不等式g(x)≥f(x)-|x-1|; 试题详情
(Ⅲ)若h(x)=g(x)- f(x)+1在[-1,1]上是增函数,求实数 f(x)+1在[-1,1]上是增函数,求实数 的取值范围. 的取值范围. 试题详情
21、设a为实数,记函数 的最大值为g(a)。 的最大值为g(a)。 试题详情
(Ⅰ)设t= ,求t的取值范围,并把f(x)表示为t的函数m(t) ,求t的取值范围,并把f(x)表示为t的函数m(t) (Ⅱ)求g(a) 试题详情
(Ⅲ)试求满足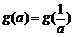 的所有实数a 的所有实数a 试题详情
 安宜高级中学2006-2007学年度第一学期 安宜高级中学2006-2007学年度第一学期
高三数学答题卡 第Ⅰ卷 选择题
(共50分) 题号 1 2 3 4 5 6 7 8 9 10 得分 答案
第Ⅱ卷 非选择题
(共100分) 11题 12题 13题 14题 15题 16题 17题解: 18题解:
试题详情
三、解答题  19题解: 19题解:
20题解: 21题解: 试题详情
ABAACBBCDB   155 155
  0 0 17、解:(Ⅰ)
 (Ⅱ)  18、解: (I) 由于在闭区间[0,7]上,只有 ,故 ,故 .若 .若 是奇函数,则 是奇函数,则 ,矛盾.所以, ,矛盾.所以, 不是奇函数. 不是奇函数. 由  , 从而知函数 , 从而知函数 是以 是以 为周期的函数. 为周期的函数.
若 是偶函数,则 是偶函数,则 .又 .又 ,从而 ,从而 . . 由于对任意的 (3,7]上, (3,7]上, ,又函数 ,又函数 的图象的关于 的图象的关于 对称,所以对区间[7,11)上的任意 对称,所以对区间[7,11)上的任意 均有 均有 .所以, .所以, ,这与前面的结论矛盾. ,这与前面的结论矛盾. 所以,函数 是非奇非偶函数. 是非奇非偶函数. (II) 由第(I)小题的解答,我们知道 在区间(0,10)有且只有两个解,并且 在区间(0,10)有且只有两个解,并且 .由于函数 .由于函数 是以 是以 为周期的函数,故 为周期的函数,故 .所以在区间[-2000,2000]上,方程 .所以在区间[-2000,2000]上,方程 共有 共有 个解. 个解. 在区间[2000,2010]上,方程 有且只有两个解.因为 有且只有两个解.因为  , ,
所以,在区间[2000,2005]上,方程 有且只有两个解. 有且只有两个解. 在区间[-2010,-2000]上,方程 有且只有两个解.因为 有且只有两个解.因为  , ,
所以,在区间[-2005,-2000]上,方程 无解. 无解. 综上所述,方程 在[-2005,2005]上共有802个解. 在[-2005,2005]上共有802个解.  19、[解](1) 19、[解](1)
(2)方程 的解分别是 的解分别是 和 和 ,由于 ,由于 在 在 和 和 上单调递减,在 上单调递减,在 和 和 上单调递增,因此 上单调递增,因此  . .
由于 . .
(3)[解法一] 当 时, 时, . .


 , ,
  . 又 . 又 , , ①
当 ,即 ,即 时,取 时,取 , ,   . .  , , 则 . .
②
当 ,即 ,即 时,取 时,取 , ,  = = . . 由 ①、②可知,当 时, 时, , , . . 因此,在区间 上, 上, 的图像位于函数 的图像位于函数 图像的上方. 图像的上方. [解法二] 当 时, 时, . . 由 得 得 , , 令  ,解得 ,解得  或 或 , ,
在区间 上,当 上,当 时, 时, 的图像与函数 的图像与函数 的图像只交于一点 的图像只交于一点 ; 当 ; 当 时, 时, 的图像与函数 的图像与函数 的图像没有交点. 的图像没有交点. 如图可知,由于直线 过点 过点 ,当 ,当 时,直线 时,直线 是由直线 是由直线 绕点 绕点 逆时针方向旋转得到. 因此,在区间 逆时针方向旋转得到. 因此,在区间 上, 上, 的图像位于函数 的图像位于函数 图像的上方. 图像的上方. 20、解:(Ⅰ)设函数 的图象上任意一点 的图象上任意一点 关于原点的对称点为 关于原点的对称点为 ,则 ,则 
∵点 在函数 在函数 的图象上 的图象上 ∴ (Ⅱ)由 当 时, 时, ,此时不等式无解 ,此时不等式无解 当 时, 时, ,解得 ,解得  因此,原不等式的解集为  (Ⅲ) ① 
② ?) ?) 
21、解:(I)∵ , , ∴要使 有意义,必须 有意义,必须 且 且 ,即 ,即 ∵ ,且 ,且 ……① ∴ ……① ∴ 的取值范围是 的取值范围是 。 。 由①得: ,∴ ,∴  , , 。 。 (II)由题意知 即为函数 即为函数  , , 的最大值, 的最大值, ∵直线 是抛物线 是抛物线  的对称轴,∴可分以下几种情况进行讨论: 的对称轴,∴可分以下几种情况进行讨论: (1)当 时,函数 时,函数 , , 的图象是开口向上的抛物线的一段, 的图象是开口向上的抛物线的一段, 由 知 知 在 在 上单调递增,故 上单调递增,故   ; ; (2)当 时, 时, , , ,有 ,有 =2; =2; (3)当 时,,函数 时,,函数 , , 的图象是开口向下的抛物线的一段, 的图象是开口向下的抛物线的一段, 若  即 即 时, 时,  , , 若  即 即 时, 时,  , , 若  即 即 时, 时,   。 。 综上所述,有 = = 。 。 (III)当 时, 时,   ; ; 当 时, 时, , , ,∴ ,∴ , ,   ,故当 ,故当 时, 时,  ; ;
当 时, 时, ,由 ,由  知: 知:  ,故 ,故 ; ; 当 时, 时, ,故 ,故 或 或 ,从而有 ,从而有 或 或 , , 要使  ,必须有 ,必须有 , , ,即 ,即 , , 此时,  。 。 综上所述,满足 的所有实数a为: 的所有实数a为: 或 或 。 。
| 
 的反函数是
的反函数是
 B.
B. C.
C. D.
D.
 的定义域是
的定义域是 B.
B.  C.
C.  D.
D.

 B.
B.  C.
C.  D.
D. 
 ,则
,则  的图像过点
的图像过点 ,其反函数的图像过点
,其反函数的图像过点 ,则
,则 等于
等于 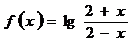 ,则
,则 的定义域为
的定义域为  B.
B.  C.
C.  D.
D. 
 在区间
在区间 内单调递增,则a的取值范围是
内单调递增,则a的取值范围是  B.
B.  C.
C. D.
D.
 密文(加密),接收方由密文
密文(加密),接收方由密文 明文(解密),已知加密规则为:明文
明文(解密),已知加密规则为:明文 对应密文
对应密文 例如,明文
例如,明文 对应密文
对应密文 当接收方收到密文
当接收方收到密文 时,则解密得到的明文为A.
时,则解密得到的明文为A. B.
B. C.
C. D.
D.
 9、如图所示,单位圆中弧AB的长为x,f(x)表示弧AB与弦AB
9、如图所示,单位圆中弧AB的长为x,f(x)表示弧AB与弦AB