
江苏省南京市2009届高三第一次调研考试
数学试题2009.3
一、填空题(本大题共14小题,每小题5分,共70分)
1、计算: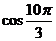 = 。
= 。
 2、若复数
2、若复数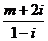
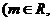
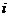 是虚数单位)为纯虚数,则
是虚数单位)为纯虚数,则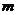 = 。
= 。
3、某人5 次上班途中所花的时间(单位:分钟)分别为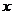 ,
,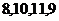 。已知这组数据的平均数为10,则其方差为 。
。已知这组数据的平均数为10,则其方差为 。
 4、已知等比数列
4、已知等比数列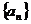 的各项均为正数,若
的各项均为正数,若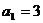 ,前三项的和为21 ,
,前三项的和为21 ,
 则
则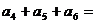 。
。
 5、设
5、设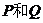 是两个集合,定义集合
是两个集合,定义集合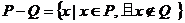 ,若
,若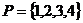 ,
,

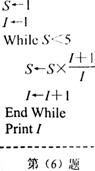
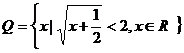 ,则
,则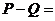 。
。
 6、根据如图所示的伪代码,可知输出的结果
6、根据如图所示的伪代码,可知输出的结果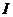 为
。
为
。




 7、已知扇形的周长为
7、已知扇形的周长为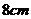 ,则该扇形面积的最大值为
,则该扇形面积的最大值为 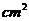 。
。
 8、过椭圆
8、过椭圆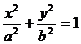
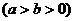 的左顶点
的左顶点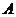 作斜率为
作斜率为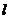 的直线,与椭圆的另一个交点为
的直线,与椭圆的另一个交点为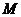 ,与
,与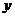 轴的交点为
轴的交点为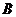 。若
。若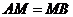 ,则该椭圆的离心率为
。
,则该椭圆的离心率为
。
 9、若方程
9、若方程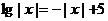 在区间
在区间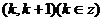 上有解,则所有满足条件的
上有解,则所有满足条件的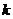 的值的和为
。
的值的和为
。




 10、如图,海岸线上有相距5海里的两座灯塔
10、如图,海岸线上有相距5海里的两座灯塔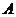 、
、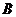 ,灯塔
,灯塔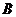 位于灯塔
位于灯塔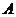 的正南方向,海上停泊着两艘轮船,甲船位于灯塔
的正南方向,海上停泊着两艘轮船,甲船位于灯塔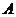 的北偏西
的北偏西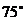 方向,与
方向,与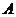 相距
相距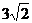 海里的
海里的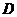 处;乙船位于灯塔B的北偏西
处;乙船位于灯塔B的北偏西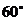 方向,与
方向,与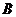 相距5海里的
相距5海里的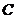 处,则两艘船之间的距离为 海里。
处,则两艘船之间的距离为 海里。

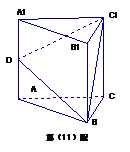 11、如图,在正三棱柱
11、如图,在正三棱柱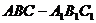 中,D为棱
中,D为棱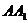 的中点,若截面
的中点,若截面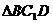 是面积为6的直角三角形,则此三棱柱的体积为
。
是面积为6的直角三角形,则此三棱柱的体积为
。






 12、设
12、设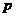 :函数
:函数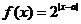 在区间
在区间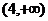 上单调递增;
上单调递增;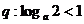 ,如果“┐p”是正真命题,那么实数
,如果“┐p”是正真命题,那么实数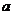 的取值范围是
。
的取值范围是
。


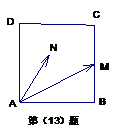 13、如图,在正方形
13、如图,在正方形 中,已知
中,已知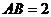 ,
,
 为
为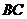 的中点,若
的中点,若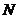 为正方形内(含边界)任意一点,则
为正方形内(含边界)任意一点,则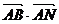 的最大值是 。
的最大值是 。
 14、已知函数
14、已知函数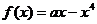 ,
,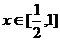 ,
,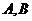 是其图象上不同的两点.若直线
是其图象上不同的两点.若直线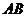 的斜率
的斜率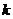 总满足
总满足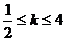 ,则实数
,则实数 的值是
。
的值是
。
 二、解答题
二、解答题
 15、(本题满分14分)
15、(本题满分14分)

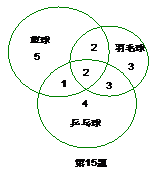 某学校篮球队,羽毛球队、乒乓球队员,某些队员不止参加了一支球队,具体情况如图所示,现从中随机抽取一名队员,求:
某学校篮球队,羽毛球队、乒乓球队员,某些队员不止参加了一支球队,具体情况如图所示,现从中随机抽取一名队员,求:
(1)  该队员只属于一支球队的概率;
该队员只属于一支球队的概率;
 (2)该队员最多属于两支球队的概率
(2)该队员最多属于两支球队的概率










 16、(本题满分14分)如图,在四棱锥
16、(本题满分14分)如图,在四棱锥 中,底面
中,底面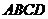 中为菱形,
中为菱形,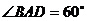 ,
,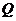 为
为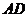 的中点。
的中点。
(1)  若
若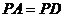 ,求证:平面
,求证:平面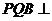 平面
平面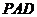 ;
;
(2) 
 点
点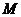 在线段
在线段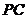 上,
上,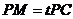 ,试确定实数
,试确定实数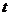 的值,使得
的值,使得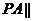 平面
平面 。
。
17、(本题满分14分)已知函数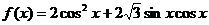 。
。
(1) 求函数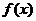 在
在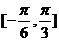 上的值域;
上的值域;
(2) 在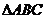 中,若
中,若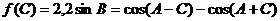 ,求
,求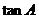 的值。
的值。
18、(本题满分16分)在平面直角坐标系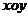 中,已知抛物线
中,已知抛物线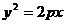 横坐标为4的点到该抛物线的焦点的距离为5。
横坐标为4的点到该抛物线的焦点的距离为5。
(1) 求抛物线的标准方程;
(2)
设点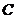 是抛物线上的动点,若以
是抛物线上的动点,若以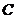 为圆心的圆在
为圆心的圆在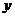 轴上截得的弦长为
轴上截得的弦长为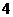 ,求证:
,求证:
圆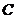 过定点。
过定点。
 19、(本题满分16分)设
19、(本题满分16分)设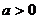 ,函数
,函数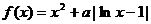 .
.
(1) 当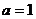 时,求曲线
时,求曲线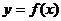 在
在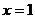 处的切线方程;
处的切线方程;
(2) 当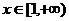 时,求函数
时,求函数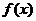 的最小值.
的最小值.
20、(本题满分16分)在数列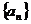 中,已知
中,已知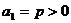 ,且,
,且,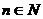
(1) 若数列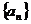 为等差数列,求
为等差数列,求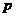 的值。
的值。
(2) 求数列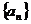 的前
的前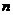 项和
项和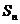
(3) 当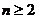 时,求证:
时,求证:
南京市2009届高三第一次调研试数学附加题
21、选做题(在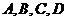 四小题中只能选做2题,每小题10分,共计2分)
四小题中只能选做2题,每小题10分,共计2分)
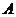 .选修
.选修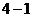 :几何证明选讲
:几何证明选讲
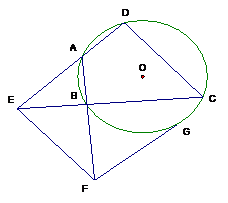 如图,已知四边形
如图,已知四边形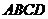 内接于⊙O,
内接于⊙O,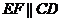 ,
,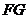 切⊙O于点
切⊙O于点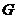 .求证:
.求证: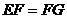 .
.
B.选修4-2:矩阵与变换
已知矩阵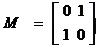 ,
,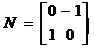 。在平面直角坐标系中,设直线
。在平面直角坐标系中,设直线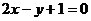 在矩阵
在矩阵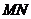 对应的变换作用下得到的曲线
对应的变换作用下得到的曲线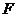 ,求曲线
,求曲线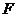 的方程。
的方程。
C.选修4-4;坐标系与参数方程
 已知直线
已知直线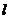 和参数方程为
和参数方程为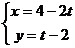
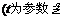 ,
,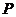 是椭圆
是椭圆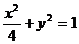 上任意一点,求点
上任意一点,求点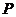 到直线
到直线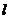 的距离的最大值。
的距离的最大值。
D.选修4-5:不等式选讲
已知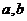 为正数,求证:
为正数,求证: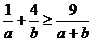 .
.
必做题:第22题、第23题每题10分,共20分。
22.已知圆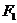 :
: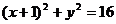 ,定点,动圆过点
,定点,动圆过点 ,且与圆
,且与圆 相内切。
相内切。
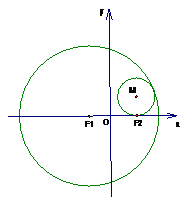 (1)求点
(1)求点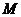 的轨迹
的轨迹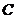 的方程;
的方程;
(2)若过原点的直线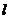 与(1)中的曲线
与(1)中的曲线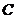 交于
交于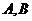 两点,且
两点,且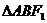 的面积为
的面积为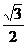 ,求直线
,求直线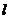 的方程。
的方程。
23已知: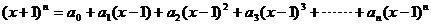
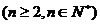
(1)当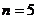 时,求
时,求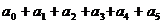 的值。
的值。
(2)设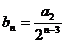 ,
,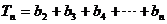 。试用数学归纳法证明:
。试用数学归纳法证明:
当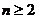 时,
时,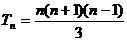
一、填空
1、 ;2、
;2、 ;3、
;3、 ;4、
;4、 ;5、
;5、 ;6、5;7、
;6、5;7、 ;8、
;8、 ;9、
;9、 ;
;
10、 ;11、
;11、 ;12、
;12、 ;13、
;13、 ;14、
;14、 。
。
二、解答题
1`5、(本题满分14分)
解:(1)(设“该队员只属于一支球队的”为事件A,则事件A的概率

(2)设“该队员最多属于两支球队的”为事件B,则事件B的概率为
答:(略)
16、(本题满分14分)
解:(1)连 ,四边形
,四边形 菱形
菱形  ,
,







 为
为 的中点,
的中点, 
又

 ,
,

 (2)当
(2)当 时,使得
时,使得 ,连
,连 交
交 于
于 ,交
,交 于
于 ,则
,则 为
为 的中点,又
的中点,又
 为
为 边
边 上中线,
上中线,
 为正三角形
为正三角形 的中心,令菱形
的中心,令菱形 的边长为
的边长为 ,则
,则 ,
, 。
。




 即:
即:
 。
。
17、解:
(1)

 ,
,

 在区间
在区间 上的值域为
上的值域为
(2)
 ,
,


 ,
,




18、解:(1)依题意,得: ,
, 。
。
抛物线标准方程为:
(2)设圆心 的坐标为
的坐标为 ,半径为
,半径为 。
。

 圆心
圆心 在
在 轴上截得的弦长为
轴上截得的弦长为


圆心 的方程为:
的方程为:
从而变为: ①
①
对于任意的 ,方程①均成立。
,方程①均成立。
故有: 解得:
解得:
所以,圆 过定点(2,0)。
过定点(2,0)。
19、解(1)当 时,
时,
令 得
得  所以切点为(1,2),切线的斜率为1,
所以切点为(1,2),切线的斜率为1,
所以曲线 在
在 处的切线方程为:
处的切线方程为: 。
。
(2)①当 时,
时, ,
,

 ,
, 恒成立。
恒成立。  在
在 上增函数。
上增函数。
故当 时,
时,
② 当 时,
时, ,
,
 (
( )
)
(i)当 即
即 时,
时, 在
在 时为正数,所以
时为正数,所以 在区间
在区间 上为增函数。故当
上为增函数。故当 时,
时, ,且此时
,且此时
(ii)当 ,即
,即 时,
时, 在
在 时为负数,在间
时为负数,在间 时为正数。所以
时为正数。所以 在区间
在区间 上为减函数,在
上为减函数,在 上为增函数
上为增函数
故当 时,
时, ,且此时
,且此时
(iii)当 ;即
;即  时,
时, 在
在 时为负数,所以
时为负数,所以 在区间[1,e]上为减函数,故当
在区间[1,e]上为减函数,故当 时,
时, 。
。
综上所述,当 时,
时, 在
在 时和
时和 时的最小值都是
时的最小值都是 。
。
所以此时 的最小值为
的最小值为 ;当
;当 时,
时, 在
在 时的最小值为
时的最小值为
 ,而
,而 ,
,
所以此时 的最小值为
的最小值为 。
。
当 时,在
时,在 时最小值为
时最小值为 ,在
,在 时的最小值为
时的最小值为 ,
,
而 ,所以此时
,所以此时 的最小值为
的最小值为
所以函数 的最小值为
的最小值为
20、解:(1)设数列 的公差为
的公差为 ,则
,则 ,
, ,
,
依题得: ,对
,对 恒成立。
恒成立。
即: ,对
,对 恒成立。
恒成立。
所以 ,即:
,即: 或
或
 ,故
,故 的值为2。
的值为2。
(2)

所以,
① 当 为奇数,且
为奇数,且 时,
时, 。
。
相乘得 所以
所以  当
当 也符合。
也符合。
② 当 为偶数,且
为偶数,且 时,
时, ,
, 
相乘得 所以
所以 
 ,所以
,所以  。因此
。因此  ,当
,当 时也符合。
时也符合。
所以数列 的通项公式为
的通项公式为 。
。
当 为偶数时,
为偶数时,


当 为奇数时,
为奇数时, 为偶数,
为偶数,


所以

南京市2009届高三第一次调研试
数学附加题参考答案
21、选做题
 .选修
.选修 :几何证明选讲
:几何证明选讲
证明:因为 切⊙O于点
切⊙O于点 ,所以
,所以
因为 ,所以
,所以 
又A、B、C、D四点共圆,所以  所以
所以 
又 ,所以
,所以 ∽
∽
所以 即
即
所以  即:
即:
B.选修4-2:矩阵与变换
解:由题设得 ,设
,设 是直线
是直线 上任意一点,
上任意一点,
点 在矩阵
在矩阵 对应的变换作用下变为
对应的变换作用下变为 ,
,
则有 , 即
, 即  ,所以
,所以
因为点 在直线
在直线 上,从而
上,从而 ,即:
,即:
所以曲线 的方程为
的方程为 
C.选修4-4;坐标系与参数方程
解: 直线 的参数方程为
的参数方程为
 为参数)故直线
为参数)故直线 的普通方程为
的普通方程为
因为 为椭圆
为椭圆 上任意点,故可设
上任意点,故可设 其中
其中 。
。
因此点 到直线
到直线 的距离是
的距离是
所以当 ,
, 时,
时, 取得最大值
取得最大值 。
。
D.选修4-5:不等式选讲
 证明:
证明: ,所以
,所以 

必做题:第22题、第23题每题10分,共20分。
22、解:(1)设圆 的半径为
的半径为 。
。
因为圆 与圆
与圆 ,所以
,所以
所以 ,即:
,即:
所以点 的轨迹
的轨迹 是以
是以 为焦点的椭圆且设椭圆方程为
为焦点的椭圆且设椭圆方程为 其中
其中  ,所以
,所以
所以曲线 的方程
的方程
(2)因为直线 过椭圆的中心,由椭圆的对称性可知,
过椭圆的中心,由椭圆的对称性可知,
因为 ,所以
,所以 。
。
不妨设点 在
在 轴上方,则
轴上方,则 。
。
所以 ,
, ,即:点
,即:点 的坐标为
的坐标为 或
或
所以直线 的斜率为
的斜率为 ,故所求直线方和程为
,故所求直线方和程为
23、(1)当 时,
时,
原等式变为

令 得
得 
(2)因为 所以
所以

①当 时。左边=
时。左边= ,右边
,右边
左边=右边,等式成立。
②假设当 时,等式成立,即
时,等式成立,即
那么,当 时,
时,
左边
 右边。
右边。
故当 时,等式成立。
时,等式成立。
综上①②,当 时,
时,
www.ks5u.com
 www.ks5u.com
www.ks5u.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com