
吉林省2009年 全真数学模拟试卷(二)
全真数学模拟试卷(二)
一、选择题(每题3分,共24分)
1. 冬季的一天室内温度是
A
2. 已知:等腰ΔABC的周长为
A
3. 圆心距为6的两圆相外切,则以这两个圆的半径为根的一元二次方程是( )
A.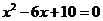 B.
B.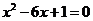
C.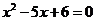 D.
D.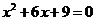
4.根据呼和浩特市第一季度用电量的扇形统计图,则二月份用电量占第一季度用电量的百分比为 ( )
A.60% B.64% C.54% D.74%
5.为了了解某校初三年级400名学生的体重情况,从中抽查了50名学生的体重进行统计分析,在这个问题中,总体是指 ( )
A.400名学生 B.被抽取的50名学生
C.400名学生的体重 D.被抽取的50名学生的体重.
6. 如图,若将ΔABC绕点C顺时针旋转90°后得到ΔA’B’C’,则A点的对应点A’的坐标是( )
A.(-3,-2) B.(2,2) C.(3,0) D.(2,1)
7.小亮观察如图1所示的两个物体,得到的俯视图是(如图2所示) ( )
A.B.C.D.
8.如图,直角梯形ABCD中,∠A=90°,∠B=45°,底边AB=5,高AD=3,点E由B沿折线BCD向点D移动,EM⊥AB于M,EN⊥AD于N,设BM=x,矩形AMRN的面积为y,那么y与x之间的函数关系的图象大致是 ( )
A.B.C.D.
二、填空题(每题3分,共18分)
9.分解因式a2b-4ab+4b=______________
10.当x__________时,有意义.
11.如图的围棋放置在某个平面直角坐标系内,白棋②的坐标为(-7,-4),白棋④的坐标为(-6,-8),那么,黑棋①的坐标应该是______________
12.如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分的面积,验证了公式___________.
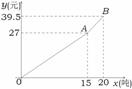
13.已知:若(a,b都是正整数),则a+b的最小值是___________.
14.如图,□ABCD中,点E在边AD上,以BE为抓痕,将ΔABE向上翻折,点A正好落中CD上的F点,若ΔFDE的周长为8,ΔFCB的周长为22,则FC的长为__________.
三、解答题(每题5分,共20分)
15. (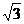 -1)0+(
-1)0+(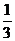 )-1-
)-1-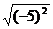 -|-1|
-|-1|
16. 先化简,再求值: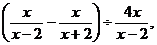 其中x=2007
其中x=2007
17.如图,某长方形广场的四角都有一块半径相同的四分之一圆形的草地,若,圆形的半径为r米,长方形长为a米,宽为b米.
(1)请用代数式表示空地的面积;
(2)若长方形长为
18.如图:PA为⊙O的切线,A为切点,PO交⊙O于点B,OA=3,OP=6,求∠BAP的度数.
四、解答题(每题6分,共12分)
19. 某旅行社为吸引市民组团去一风景区旅游,推出了如下收费标准:如果人数不超过25人,人均旅游费用为1000元;如果为为超过25人,每增加1个人,人均旅游费用降低20元,但人均旅游费用不得低于700元.某单位组织员工去该风景区旅游,共支付给施行社旅游费用27000元,请问该单位这次共有多少员工去风景区旅游?
20. 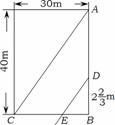 如图,在一个长
如图,在一个长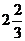 m的D 处时,他和王刚在阳光下的影子恰好重叠在同一条直线上。此时,A处一根电线杆在阳光下的影子也恰好落在对角线AC上。
m的D 处时,他和王刚在阳光下的影子恰好重叠在同一条直线上。此时,A处一根电线杆在阳光下的影子也恰好落在对角线AC上。
(1)求他们的影子重叠时,两人相距多少米(DE的长)?
(2)求张华追赶王刚的速度是多少(精确到
五、解答题(每题6分,共12分)
21.  如图所示,把一个直角三角尺ABC绕着30º角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合。
如图所示,把一个直角三角尺ABC绕着30º角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合。
(1)三角尺旋转了多少度?
(2)连结CD,试判断ΔCBD的形状;
(3)求∠BDC的度数。
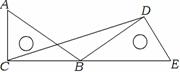
 22. 某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交水费y(元)与用水量x(吨)的函数关系如图所示。
22. 某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交水费y(元)与用水量x(吨)的函数关系如图所示。
(1)分别写出当0≤x≤15和x≥15时,y与x的函数关系式;
(2)若某用户该月用水21吨,则应交水费多少元?
六、解答题(每题7分,共14分)
23.如图,点P是圆上的一个动点,弦AB=,PC是∠APB的平分线,∠BAC=30°.
(1)当∠PAC等于多少度时,四边形PACB有最大面积?最大面积是多少?
(2)当∠PAC等于多少度时,四边形PACB是梯形?说明你的理由.
24.为选派一名学生参加全市实践活动技能竞赛,A,B两位同学在校实习基地现场进行加工直径为20┨的零件的测试,他俩各加工的10个零件的相关数据依次如右图表所示(单位:mm).
根据测试得到的有关数据,试解答下列问题:
(1)考虑平均数与完全符合要求的个数,你认为_________的成绩好些.
(2)计算出的大小,考虑平均数与方差,说明谁的成绩好些.
(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个实际情况,你认为派谁去参赛较合适?说明你的理由.
七、解答题(每题10分,共20分)
25.正方形OCED与扇形AOB有公共顶点O,分别以OA,OB所在直线为x轴,y轴,建立平面直角坐标系,如图所示.正方形两个顶点C,D分别在x轴,y轴正半轴上移动.设OC=x,OA=3.
(1)当x=1时,正方形与扇形不重合的面积是__________;些时直线CD对应的函数关系式是_____________;
(2)当直线CD与扇形AOB相切时,求直线CD对应的函数关系式;
(3)当正方形有顶点恰好落在上时,求正方形与扇形不重合的面积.
26.矩形OABC在直角坐标系中的位置如图所示,A,C两点的坐标分别为A(6,0)C(0,3),直线与BC边相交于点D.
(1)求点D的坐标;
(2)若抛物线y=ax2+bx经过D,A两点,试确定些抛物线的表达式;
(3)若P为x轴上方(2)中抛物线上一点,求ΔPOA面积的最大值;
(4)设(2)中抛物线的对称轴与直线OD交于点M,点Q为对称轴上一动点,以Q,O,M为顶点的三角形与ΔOCD相似,求符合条件的Q点的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com