2009年高考数学难点突破专题辅导一
难点1 集合思想及应用
集合是高中数学的基本知识，为历年必考内容之一，主要考查对集合基本概念的认识和理解，以及作为工具，考查集合语言和集合思想的运用.本节主要是帮助考生运用集合的观点，不断加深对集合概念、集合语言、集合思想的理解与应用.
●难点磁场
(★★★★★)已知集合A={(x,y)|x2+mx－y+2=0},B={(x,y)|x－y+1=0,且0≤x≤2},如果A∩B≠
,求实数m的取值范围.
●案例探究
［例1］设A={(x,y)|y2－x－1=0},B={(x,y)|4x2+2x－2y+5=0},C={(x,y)|y=kx+b},是否存在k、b∈N,使得(A∪B)∩C=，证明此结论.
命题意图：本题主要考查考生对集合及其符号的分析转化能力，即能从集合符号上分辨出所考查的知识点，进而解决问题.属★★★★★级题目.
知识依托：解决此题的闪光点是将条件(A∪B)∩C=转化为A∩C=且B∩C=，这样难度就降低了.
错解分析：此题难点在于考生对符号的不理解，对题目所给出的条件不能认清其实质内涵，因而可能感觉无从下手.
技巧与方法：由集合A与集合B中的方程联立构成方程组，用判别式对根的情况进行限制，可得到b、k的范围，又因b、k∈N,进而可得值.
解：∵(A∪B)∩C=，∴A∩C=且B∩C=
∵
∴k2x2+(2bk－1)x+b2－1=0
∵A∩C=
∴Δ1=(2bk－1)2－4k2(b2－1)<0
∴4k2－4bk+1<0,此不等式有解，其充要条件是16b2－16>0,即b2>1 ①
∵
∴4x2+(2－2k)x+(5+2b)=0
∵B∩C=,∴Δ2=(1－k)2－4(5－2b)<0
∴k2－2k+8b－19<0,从而8b<20,即b<2.5 ②
由①②及b∈N,得b=2代入由Δ1<0和Δ2<0组成的不等式组，得
∴k=1,故存在自然数k=1,b=2,使得(A∪B)∩C=.
［例2］向50名学生调查对A、B两事件的态度，有如下结果：赞成A的人数是全体的五分之三，其余的不赞成，赞成B的比赞成A的多3人，其余的不赞成；另外，对A、B都不赞成的学生数比对A、B都赞成的学生数的三分之一多1人.问对A、B都赞成的学生和都不赞成的学生各有多少人？
命题意图：在集合问题中，有一些常用的方法如数轴法取交并集，韦恩图法等，需要考生切实掌握.本题主要强化学生的这种能力.属★★★★级题目.
知识依托：解答本题的闪光点是考生能由题目中的条件，想到用韦恩图直观地表示出来.
错解分析：本题难点在于所给的数量关系比较错综复杂，一时理不清头绪，不好找线索.
技巧与方法：画出韦恩图，形象地表示出各数量关系间的联系.
解：赞成A的人数为50×
=30，赞成B的人数为30+3=33，如上图，记50名学生组成的集合为U，赞成事件A的学生全体为集合A；赞成事件B的学生全体为集合B.
设对事件A、B都赞成的学生人数为x,则对A、B都不赞成的学生人数为
+1,赞成A而不赞成B的人数为30－x，赞成B而不赞成A的人数为33－x.
依题意(30－x)+(33－x)+x+(+1)=50,解得x=21.
所以对A、B都赞成的同学有21人，都不赞成的有8人.
●锦囊妙计
1.解答集合问题，首先要正确理解集合有关概念，特别是集合中元素的三要素；对于用描述法给出的集合{x|x∈P},要紧紧抓住竖线前面的代表元素x以及它所具有的性质P；要重视发挥图示法的作用，通过数形结合直观地解决问题.
2.注意空集的特殊性，在解题中，若未能指明集合非空时，要考虑到空集的可能性，如A
B,则有A=或A≠两种可能，此时应分类讨论.
●歼灭难点训练
一、选择题
1.(★★★★)集合M={x|x=
,k∈Z},N={x|x=
,k∈Z},则( )
A.M=N B.M
N C.M
N D.M∩N=
2.(★★★★)已知集合A={x|－2≤x≤7},B={x|m+1<x<2m－1}且B≠,若A∪B=A，则( )
A.－3≤m≤4 B.－3<m<4
C.2<m<4 D.2<m≤4
二、填空题
3.(★★★★)已知集合A={x∈R|ax2－3x+2=0,a∈R},若A中元素至多有1个，则a的取值范围是_________.
4.(★★★★)x、y∈R,A={(x,y)|x2+y2=1},B={(x,y)|
=1,a>0,b>0},当A∩B只有一个元素时，a,b的关系式是_________.
三、解答题
5.(★★★★★)集合A={x|x2－ax+a2－19=0},B={x|log2(x2－5x+8)=1}，C={x|x2+2x－8=0},求当a取什么实数时，A∩B
和A∩C=同时成立.
6.(★★★★★)已知{an}是等差数列，d为公差且不为0，a1和d均为实数，它的前n项和记作Sn,设集合A={(an,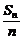
)|n∈N*},B={(x,y)|
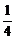x2－y2=1,x,y∈R}.
试问下列结论是否正确，如果正确，请给予证明；如果不正确，请举例说明.
(1)若以集合A中的元素作为点的坐标，则这些点都在同一条直线上；
(2)A∩B至多有一个元素；
(3)当a1≠0时，一定有A∩B≠.
7.(★★★★)已知集合A={z||z－2|≤2,z∈C},集合B={w|w=
zi+b,b∈R},当A∩B=B时，求b的值.
8.(★★★★)设f(x)=x2+px+q,A={x|x=f(x)},B={x|f［f(x)］=x}.
(1)求证：A
B;
(2)如果A={－1，3}，求B.
难点磁场
解：由
得x2+(m－1)x+1=0 ①
∵A∩B≠
∴方程①在区间［0，2］上至少有一个实数解.
首先，由Δ=(m－1)2－4≥0,得m≥3或m≤－1,当m≥3时，由x1+x2=－(m－1)＜0及x1x2=1>0知，方程①只有负根，不符合要求.
当m≤－1时，由x1+x2=－(m－1)>0及x1x2=1>0知，方程①只有正根，且必有一根在区间(0，1］内，从而方程①至少有一个根在区间［0，2］内.
故所求m的取值范围是m≤－1.
歼灭难点训练
一、1.解析：对M将k分成两类：k=2n或k=2n+1(n∈Z),M={x|x=nπ+
,n∈Z}∪{x|x=
nπ+
,n∈Z},对N将k分成四类，k=4n或k=4n+1,k=4n+2,k=4n+3(n∈Z),N={x|x=nπ+
,n∈Z}∪{x|x=nπ+,n∈Z}∪{x|x=nπ+π,n∈Z}∪{x|x=nπ+
,n∈Z}.
答案：C
2.解析：∵A∪B=A，∴BA,又B≠,
∴
即2＜m≤4.
答案：D
二、3.a=0或a≥
4.解析：由A∩B只有1个交点知，圆x2+y2=1与直线
=1相切，则1=
,即ab=
.
答案：ab=
三、5.解：log2(x2－5x+8)=1,由此得x2－5x+8=2，∴B={2,3}.由x2+2x－8=0，∴C={2,－4},又A∩C=，∴2和－4都不是关于x的方程x2－ax+a2－19=0的解，而A∩B 
,即A∩B≠,
∴3是关于x的方程x2－ax+a2－19=0的解，∴可得a=5或a=－2.
当a=5时，得A={2，3}，∴A∩C={2}，这与A∩C=不符合，所以a=5(舍去)；当a=－2时，可以求得A={3，－5}，符合A∩C=，A∩B ，∴a=－2.
6.解：(1)正确.在等差数列{an}中，Sn=
,则
(a1+an),这表明点(an,
）的坐标适合方程y
(x+a1),于是点(an, )均在直线y=
x+a1上.
(2)正确.设(x,y)∈A∩B,则(x,y)中的坐标x,y应是方程组
的解，由方程组消去y得：2a1x+a12=－4(*)，当a1=0时，方程(*)无解，此时A∩B=；当a1≠0时，方程(*)只有一个解x=
,此时，方程组也只有一解
,故上述方程组至多有一解.
∴A∩B至多有一个元素.
(3）不正确.取a1=1,d=1,对一切的x∈N*,有an=a1+(n－1)d=n>0, >0,这时集合A中的元素作为点的坐标，其横、纵坐标均为正，另外，由于a1=1≠0.如果A∩B≠,那么据(2）的结论，A∩B中至多有一个元素(x0,y0）,而x0=
＜0,y0=
＜0,这样的(x0,y0）
A,产生矛盾，故a1=1,d=1时A∩B=，所以a1≠0时，一定有A∩B≠是不正确的.
7.解：由w=zi+b得z=
,
∵z∈A,∴|z－2|≤2,代入得|－2|≤2,化简得|w－(b+i)|≤1.
∴集合A、B在复平面内对应的点的集合是两个圆面，集合A表示以点(2，0）为圆心，半径为2的圆面，集合B表示以点(b,1)为圆心，半径为1的圆面.
又A∩B=B，即BA，∴两圆内含.
因此
≤2－1,即(b－2)2≤0，∴b=2.
8.(1)证明：设x0是集合A中的任一元素，即有x0∈A.
∵A={x|x=f(x)},∴x0=f(x0).
即有f［f(x0)］=f(x0)=x0,∴x0∈B,故AB.
(2)证明：∵A={－1,3}={x|x2+px+q=x},
∴方程x2+(p－1)x+q=0有两根－1和3，应用韦达定理，得
∴f(x)=x2－x－3.
于是集合B的元素是方程f［f(x)］=x,也即(x2－x－3)2－(x2－x－3)－3=x(*)的根.
将方程(*)变形，得(x2－x－3）2－x2=0
解得x=1,3,
,－.
故B={－，－1，，3}.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com