
2009届高考数学第三轮复习精编模拟十二
参考公式:
如果事件 互斥,那么
球的表面积公式
互斥,那么
球的表面积公式


如果事件 相互独立,那么
其中
相互独立,那么
其中 表示球的半径
表示球的半径
 球的体积公式
球的体积公式
如果事件 在一次试验中发生的概率是
在一次试验中发生的概率是 ,那么
,那么 
 次独立重复试验中事件
次独立重复试验中事件 恰好发生
恰好发生 次的概率 其中
次的概率 其中 表示球的半径
表示球的半径

第一部分 选择题(共50分)
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的
1.设集合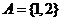 ,则满足
,则满足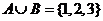 的集合B的个数是( )。
的集合B的个数是( )。
A.1 B.
 2
2 复数
复数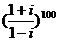 的值等于 ( )
的值等于 ( )
A.1 B.-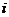 D.
D.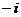
3.设函数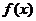 在
在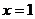 处连续,且
处连续,且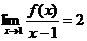 ,则
,则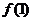 等于 ( )
等于 ( )
A.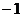 B.
B. C.
C.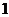 D.
D.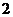
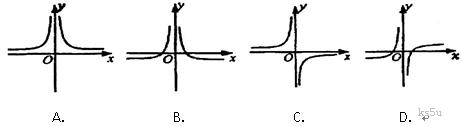
4.函数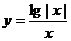 的图象大致是 ( )
的图象大致是 ( )
5.设等差数列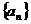 的公差为2,前
的公差为2,前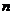 项和为
项和为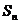 ,则下列结论中正确的是 ( )
,则下列结论中正确的是 ( )
A.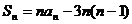 B.
B.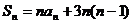
C. D.
D.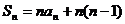
6.若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“同族函数”,那么函数解析式为 ,值域为
,值域为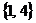 的“同族函数”共有 ( )
的“同族函数”共有 ( )
A.7个 B.8个 C.9个 D.10个
7.6支签字笔与3本笔记本的金额之和大于24元,而4支签字笔与5本笔记本的金额之和小于22元,则2支签字笔与3本笔记本的金额比较结果是 ( )
A.3本笔记本贵 B.2支签字笔贵 C.相同 D.不确定
8.球面上有三点,其中任意两点的球面距离都等于球的大圆周长的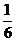 ,经过这三点的小圆的周长为
,经过这三点的小圆的周长为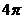 ,则这个球的表面积为 ( )
,则这个球的表面积为 ( )
A.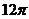 B.
B.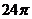 C.
C. D.
D.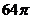
 9.如图,在
9.如图,在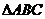 中,
中,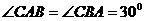 ,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为 ( )
,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为 ( )
A.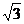 B.
B.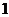
C.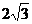 D.
D.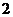
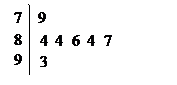 10.下图是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )。
10.下图是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )。
A.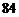 ,
,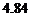 B.
B.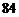 ,
,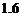
C.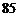 ,
,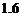 D.
D.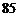 ,
,
第二部分 非选择题(共100分)
二、填空题:本大题共5小题,其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.每小题5分,满分20分.
则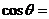 .
.
12.如图,一条直角走廊宽为
板面为矩形,宽为
度不能超过 米.
 13.如图,在正方体ABCD―A1B
13.如图,在正方体ABCD―A1B
是BC的中点,则D1B与AM所成角的余弦值
是 .
 14、(坐标系与参数方程选做题) 直线
14、(坐标系与参数方程选做题) 直线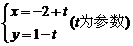 被圆
被圆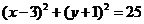 所截得的弦长为
.
所截得的弦长为
.
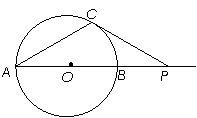
15.(几何证明选讲选做题) 15、如图,⊙O的直径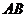 =
=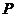 是
是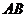 延
延
长线上的一点,过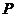 点作⊙O的切线,切点为
点作⊙O的切线,切点为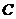 ,连接
,连接 ,
,
若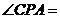 30°,PC =
。
30°,PC =
。
三.解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.
16.(本题满分12分)将A、B两枚骰子各抛掷一次,观察向上的点数,问:
(I)共有多少种不同的结果?
(II)两枚骰子点数之和是3的倍数的结果有多少种?
(III)两枚骰子点数之和是3的倍数的概率是多少?
17.(本小题满分12分)已知函数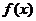 是定义在
是定义在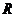 上的偶函数,当
上的偶函数,当 时,
时,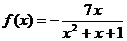 .
.
(1)求当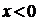 时
时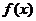 的解析式;
的解析式;
(2)试确定函数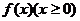 的单调区间,并证明你的结论;
的单调区间,并证明你的结论;
(3)若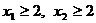 且
且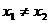 ,证明:
,证明: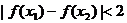 .
.
18.(本小题满分14分)在四棱锥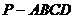 中,
中,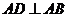 ,
,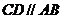 ,
,
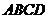 成
成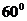 角,点
角,点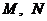 分别是
分别是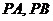 的中点.
的中点.
(1)求二面角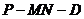 的大小;
的大小;
(2)当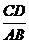 的值为多少时,
的值为多少时,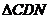 为直角三角形.
为直角三角形.

19.(本小题满分14分)已知在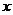 轴上有一点列:
轴上有一点列: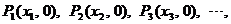
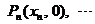 ,点
,点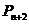 分有向线段
分有向线段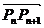 所成的比为
所成的比为 ,其中
,其中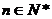 ,
,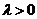 为
为
常数,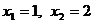 .
.
(1)设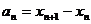 ,求数列
,求数列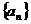 的通项公式;
的通项公式;
(2)设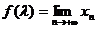 ,当
,当 变化时,求
变化时,求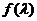 的取值范围.
的取值范围.
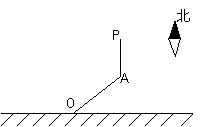 20.(本小题满分14分)在东西方向直线延伸的湖岸上有一港口O,一艘机艇以
20.(本小题满分14分)在东西方向直线延伸的湖岸上有一港口O,一艘机艇以
21.(本小题满分14分)如图,设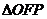 的面积为
的面积为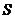 ,已知
,已知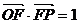 .
.
(1)若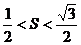 ,求向量
,求向量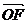 与
与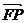 的夹角
的夹角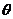 的取值范围;
的取值范围;
(2)若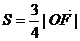 ,且
,且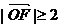 ,当
,当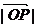 取最小值时,建立适当的直角坐标系,求
取最小值时,建立适当的直角坐标系,求
以 为中心,
为中心,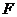 为一个焦点且经过点
为一个焦点且经过点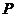 的椭圆方程.
的椭圆方程.
 |
一.选择题:CADDC CBCAC
解析:1.解: ,
, ,则集合B中必含有元素3,即此题可转化为求集合
,则集合B中必含有元素3,即此题可转化为求集合 的子集个数问题,所以满足题目条件的集合B共有
的子集个数问题,所以满足题目条件的集合B共有 个。故选择答案C。
个。故选择答案C。
2.只要注意到 ,即可迅速得到答案.
,即可迅速得到答案.
3.特殊值法, 令 , 得
, 得 .
.
4.应注意到函数 是奇函数, 可排除A, B选项, 代数值
是奇函数, 可排除A, B选项, 代数值 检验即得D.
检验即得D.
5.可理解为首项是 ,公差是
,公差是 的等差数列
的等差数列 ,故
,故

6.由题意知同族函数的定义域非空, 且由 中的两个(这里
中的两个(这里 和
和 中各有一个), 或三个, 或全部元素组成, 故定义域的个数为
中各有一个), 或三个, 或全部元素组成, 故定义域的个数为 .
.
7.设签字笔与笔记本的价格分别是 , 2支签字笔与3本笔记本的金额比较结果是
, 2支签字笔与3本笔记本的金额比较结果是 , 即
, 即
 ,已知
,已知 ,
, ,在直角坐标系中画图,可知直线
,在直角坐标系中画图,可知直线 的斜率始终为负, 故有
的斜率始终为负, 故有 , 所以选B
, 所以选B
8.由已知得小圆半径 , 三点组成正三角形, 边长为球的半径
, 三点组成正三角形, 边长为球的半径 , 所以有
, 所以有
 ,
,  , 所以球的表面积
, 所以球的表面积 .
.
9.设 , 则在椭圆中, 有
, 则在椭圆中, 有 ,
,  , 而在双曲线中, 有
, 而在双曲线中, 有
 ,
,  , ∴
, ∴
10. 解:5个有效分为84,84,86,84,87;其平均数为85。利用方差公式可得方差为1.6.
二.填空题:11、 ; 12、
; 12、 ; 13、
; 13、 ; 14、
; 14、 ;15、
;15、 ;
;
解析:
11.解:设向量 与
与 的夹角为
的夹角为 且
且 ∴
∴ ,则
,则
 =
= .
.
12. 设 , 则有
, 则有 ,
,
根据小车的转动情况, 可大胆猜测只有 时,
时,  .
.
13. 设正方体的棱长为 , 过
, 过 点作直线
点作直线 交
交 的延长线于
的延长线于 , 连
, 连 , 在
, 在 中,
中,  ,
,  ,
,  , ∴
, ∴ 
14. 解:把直线 代入
代入 得
得
 ,弦长为
,弦长为
15.解:连接 ,PC是⊙O的切线,∴∠OCP=Rt∠.
,PC是⊙O的切线,∴∠OCP=Rt∠.
∵ 30°,OC=
30°,OC= =3, ∴
=3, ∴ ,即PC=
,即PC= .
.
三.解答题:
16.解: (I) 共有 种结果 ………………4分
种结果 ………………4分
(II) 若用(a,b)来表示两枚骰子向上的点数,则点数之和是3的倍数的结果有:
(1,2),(2,1),(1,5),(5,1),(2,4),(4,2),
(3,3),(4,5),(5,4),(3,6),(6,3),(6,6)
共12种. ………………8分
(III)两枚骰子点数之和是3的倍数的概率是:P= …………12分
…………12分
17.(1)若 ,则
,则 , ∵函数
, ∵函数 是定义在
是定义在 上的偶函数,
上的偶函数,
∴  ----------3分
----------3分
(2)当 时,
时, . --------------6分
. --------------6分
显然当 时,
时, ;当
;当 时,
时, ,又
,又 在
在 和
和 处连续,
处连续,
∴函数 在
在 上为减函数,在
上为减函数,在 上为增函数. -----------8分
上为增函数. -----------8分
(3)∵函数 在
在 上为增函数,且
上为增函数,且 ,
,
∴当 时,有
时,有 ,------------------10分
,------------------10分
又当 时,得
时,得 且
且 , 即
, 即
∴ 即得
即得 .
----------12分
.
----------12分
18.(1)由已知 , 得
, 得 平面
平面 ,
,
又 , ∴
, ∴ 平面
平面 ,
, 
∴ 为二面角
为二面角 的平面角.
----------3分
的平面角.
----------3分
由已知 , 得
, 得 ,
,
∵ 是
是 斜边
斜边 上的中线,
上的中线, 
∴ 为等腰三角形,
为等腰三角形,  ,
,
即二面角 的大小为
的大小为 .
-------------7分
.
-------------7分
(2)显然 . 若
. 若 , 则
, 则 平面
平面 ,
,
而 平面
平面 ,故平面
,故平面 与平面
与平面 重合,与题意不符.
重合,与题意不符.
由 是
是 ,则必有
,则必有 ,
,
连BD,设 ,由已知得
,由已知得 ,从而
,从而 ,
,
又 ,∴
,∴ ,得
,得 ,
,
故 平面
平面 ,
-----------10分
,
-----------10分
∴ ,又
,又 ,∴
,∴ 平面
平面 , ∴
, ∴ ,反之亦然.
,反之亦然.
∵ ∴
∴  , ∴
, ∴ ∽
∽ -------12分
-------12分
∴ .
--------14分
.
--------14分
19.(1)由题意得 ,
,
 -----------3分
-----------3分
又 , ∴数列
, ∴数列 是首项为
是首项为 、公比为
、公比为 的等比数列,-----------6分
的等比数列,-----------6分
∴ --------------7分
--------------7分
(2)∵ ,
, 
∴ ,
,  ---------12分
---------12分
∴当 时,
时,  ------------14分
------------14分
20.以 为原点,湖岸线为
为原点,湖岸线为 轴建立直角坐标系, 设OA的倾斜角为
轴建立直角坐标系, 设OA的倾斜角为 ,点P的坐标为
,点P的坐标为 ,
,
 ,则有
………………3分
,则有
………………3分
 -------------7分
-------------7分
由此得 -------------9分
-------------9分
即  -------------12分
-------------12分
故营救区域为直线 与圆
与圆 围城的弓形区域.(图略)--------14分
围城的弓形区域.(图略)--------14分
21.(1)由题意知 , 可得
, 可得 .--------2分
.--------2分
∵ , ∴
, ∴ , 有
, 有 . --------4分
. --------4分
(2)以 为原点,
为原点, 所在直线为
所在直线为 轴建立直角坐标系,
轴建立直角坐标系,
设 ,点
,点 的坐标为
的坐标为 ,
-------5分
,
-------5分
∵ , ∴
, ∴ ,
,  . -------6分
. -------6分
∴ , ∴
, ∴ . ------8分
. ------8分
设 ,则当
,则当 时,有
时,有 .
.
∴ 在
在 上增函数,∴当
上增函数,∴当 时,
时, 取得最小值
取得最小值 ,
,
从而 取得最小,此时
取得最小,此时 . ---------------------11分
. ---------------------11分
设椭圆方程为 ,
,
则 ,解之得
,解之得 ,故
,故 .--------14分
.--------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com