1,3,5 A.点M在线段AB上 B.点B在线段AM上 C.点A在线段BM上
D.O、A、B、M四点共线
试题详情
8.二次函数 则实数a的取值范围是( ) 则实数a的取值范围是( ) 试题详情
试题详情
试题详情
试题详情
试题详情
11.
试题详情
12.已知x,y满足约束条件 的最大值为
. 的最大值为
. 试题详情
试题详情
14.关于x的方程| 有三个不相等的实数根,则实数a=__________ 有三个不相等的实数根,则实数a=__________ 试题详情
试题详情
f(x)=max 的最大值与最小值的差是____________. 的最大值与最小值的差是____________. 三.解答题 试题详情
16.(本题12分) 已知函数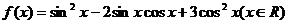 (1)说明函数y=f(x)图像可由y=cos2x的图像经过怎样的变换得到; 试题详情
(2)当 时,求函数f(x)的最大值和最小值 时,求函数f(x)的最大值和最小值 试题详情
试题详情
已知O为坐标原点,  , , 试题详情
若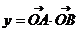 试题详情
试题详情
试题详情
18.(本题12分)△ABC中,角A、B、C所对边的长分别是a、b、c,且cos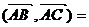  . . 试题详情
(1)求 的值; 的值; 试题详情
(2)若 ,且 ,且 ,求b、c的值. ,求b、c的值. 试题详情
试题详情
试题详情
试题详情
(2)求数列 的前n项和 的前n项和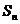 试题详情
试题详情
(Ⅰ)求该出版社一年的利润 (万元)与每本书的定价 (万元)与每本书的定价 的函数关系式; 的函数关系式; 试题详情
(Ⅱ)当每本书的定价为多少元时,该出版社一年的利润 最大,并求出 最大,并求出 的最大值 的最大值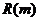 试题详情
试题详情
设函数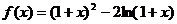 试题详情
(1)求 的单调增区间和单调减区间; 的单调增区间和单调减区间; 试题详情
(2)若当 时(其中e=2.71828…),不等式 时(其中e=2.71828…),不等式 恒成立,求实数m的取值范围; 恒成立,求实数m的取值范围; 试题详情
(3)若关于x的方程 上恰有两个相异的实根,求实数a的取值范围。 上恰有两个相异的实根,求实数a的取值范围。 2009届厦门双十中学数学(理)第一次月考答卷 说明:大题的答案必须写在虚线内,否则无效;必须用黑色签字笔书写
总成绩
试题详情
二、填空题:
试题详情
试题详情
试题详情
试题详情
一选择题:DAADB
CBDDC 二.填空题:11. 1 ;
12.5 13.  14. 1; 15.5 14. 1; 15.5 16.解:(1) …………4分 …………4分 将y=cos2x的图象先向左平移 个单位长度,再将所得图像上的点的横坐标保持不变,纵坐标伸长为原来的 个单位长度,再将所得图像上的点的横坐标保持不变,纵坐标伸长为原来的 倍,最后将所得图像向上平移2个单位即可.………………………………………………7分 倍,最后将所得图像向上平移2个单位即可.………………………………………………7分 (2)  …………9分 …………9分  即 即 ……………………11分 ……………………11分
∴函数f(x)的最小值为3,最大值为 …………………………………………………12分 …………………………………………………12分 17.解:(1)  ;……………………5分 ;……………………5分
由 ,得 ,得 , , ∴ 的单调减区间是 的单调减区间是 ;阶段 ………………8分 ;阶段 ………………8分 (2)当 时, 时, , , ∴在 时, 时, 取最大值 取最大值 ,由 ,由 ,得 ,得 。…………12分 。…………12分 18.解析:(1) = = ……2’
……2’ = ………… 6’ ………… 6’ (2)由余弦定理,得 即 …………………………………… 8’ …………………………………… 8’   ……………………10’ ……………………10’
 可求得 可求得 ………………………………… 12’ ………………………………… 12’
19.解:(I) 公差为 ,公比为 ,公比为 。 。 由条件: ,得 ,得 ……………………4分 ……………………4分  ………………………………………………6分 ………………………………………………6分 (II)由(1)可知  ……………………(1) ……………………(1)
 ………………………(2) ………………………(2)
由(2)-(1)得  …………………………9分 …………………………9分

 …………………………………………………………12分 …………………………………………………………12分
20.解:(Ⅰ)该出版社一年的利润 (万元)与每本书定价 (万元)与每本书定价 的函数关系式为: 的函数关系式为:  .……………………4分(定义域不写扣2分) .……………………4分(定义域不写扣2分) (Ⅱ)  .…………………………6分 .…………………………6分 令 得 得 或x=20(不合题意,舍去).…………7分 或x=20(不合题意,舍去).…………7分  , ,  . . 在 两侧 两侧 的值由正变负. 的值由正变负. 所以(1)当 即 即 时, 时,  .……9分 .……9分 (2)当 即 即 时, 时,  ,…………………………11分 ,…………………………11分
所以 答:若 ,则当每本书定价为 ,则当每本书定价为 元时,出版社一年的利润 元时,出版社一年的利润 最大,最大值 最大,最大值 (万元);若 (万元);若 ,则当每本书定价为11元时,出版社一年的利润 ,则当每本书定价为11元时,出版社一年的利润 最大,最大值 最大,最大值 (万元).…………………………13分 (万元).…………………………13分 21.解:(1)函数定义域为 ………………………………2分 ………………………………2分 ∵ 由 ∴增区间:(0,+∞),减区间:(-1,0)………………………………5分 (2)由 
∵ ……………………8分 ……………………8分 ∴ ∴ 时, 时, 恒成立。………………………………………………10分 恒成立。………………………………………………10分 (3)  ……………………11分 ……………………11分
∵ 由 由  , ,
故 上恰有两相异实根 上恰有两相异实根  ……………………………………14分 ……………………………………14分
| 
 是整数”的逆命题是( )
是整数”的逆命题是( ) 是整数,则
是整数,则 B.若
B.若 是奇数,则
是奇数,则
 是偶数,则
是偶数,则 D. 若
D. 若 能被3整除,则
能被3整除,则
 共线,则p是q的 ( )
共线,则p是q的 ( ) ,
, 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, 的图象如图所示,则不等式
的图象如图所示,则不等式 的解集是(
)
的解集是(
) A.
A.



 的直线l经过圆:
的直线l经过圆: 的圆心,则直线l的倾斜角大小为( )
的圆心,则直线l的倾斜角大小为( )