
第一讲 函数定义域和值域
★★★高考在考什么
【考题回放】
1.函数f(x)= 的定义域是 ( A )
的定义域是 ( A )
A. -∞,0] B.[0,+∞
-∞,0] B.[0,+∞ C.(-∞,0) D.(-∞,+∞)
C.(-∞,0) D.(-∞,+∞)
2.函数 的定义域为 (A )
的定义域为 (A )
A.(1,2)∪(2,3) B.
C.(1,3) D.[1,3]
3. 对于抛物线线 上的每一个点
上的每一个点 ,点
,点 都满足
都满足 ,则
,则 的取值范围是
( B )
的取值范围是
( B )
 .
.
 .
.
 .
.
 .
.
4.已知 的定义域为
的定义域为 ,则
,则 的定义域为
的定义域为  。
。
5. 不等式 对一切非零实数x总成立 , 则
对一切非零实数x总成立 , 则 的取值范围是
的取值范围是
 __。
__。
6. 已知二次函数 的导数为
的导数为 ,
, ,对于任意实数
,对于任意实数 ,有
,有 ,则
,则 的最小值为 。
的最小值为 。
★★★高考要考什么
一、 函数定义域有两类:具体函数与抽象函数
抽象函数:(1)已知 的定义域为D,求
的定义域为D,求 的定义域;(由
的定义域;(由 求得
求得 的范围就是)
的范围就是)
(2)已知 的定义域为D,求
的定义域为D,求 的定义域;(
的定义域;( 求出
求出 的范围就是)
的范围就是)
二、 函数值域(最值)的求法有:
直观法:图象在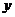 轴上的“投影”的范围就是值域的范围;
轴上的“投影”的范围就是值域的范围;
配方法:适合一元二次函数
反解法:有界量用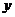 来表示。如
来表示。如 ,
, ,
, 等等。如,
等等。如, 。
。
换元法:通过变量代换转化为能求值域的函数,特别注意新变量的范围。注意三角换元的应用。
如求 的值域。
的值域。
单调性:特别适合于指、对数函数的复合函数。如求 值域。
值域。
注意函数 的单调性。
的单调性。
基本不等式:要注意“一正、二定、三相等”,
判别式:适合于可转化为关于 的一元二次方程的函数求值域。如
的一元二次方程的函数求值域。如 。
。
反之:方程有解也可转化为函数求值域。如方程 有解,求
有解,求 的范围。
的范围。
数形结合:要注意代数式的几何意义。如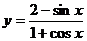 的值域。(几何意义??斜率)
的值域。(几何意义??斜率)
三、 恒成立和有解问题
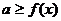 恒成立
恒成立 的最大值;
的最大值;
 恒成立
恒成立 的最小值;
的最小值;
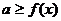 有解
有解 的最小值;
的最小值; 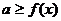 无解
无解 的最小值;
的最小值;
★★★ 突 破 重 难 点
【范例1】已知f(x)=3x-b(2≤x≤4,b为常数)的图象经过点(2,1),求F(x)=[f-1(x)]2-f-1(x2)的值域。
分析提示:求函数值域时,不但要重视对应法则的作用,而且要特别注意定义域的制约作用。本题要注意F(x)的定义域与f-1(x)定义域的联系与区别。
解:由图象经过点(2,1)得, ,
, 


 F(x)=[f-1(x)]2-f-1(x2)
F(x)=[f-1(x)]2-f-1(x2) 
 的定义域为
的定义域为 

 ,
,  ,
,  的值域是
的值域是
变式: 函数 的定义域为
的定义域为 ,图象如图所示,
,图象如图所示,
其反函数为 则不等式
则不等式
的解集为  .
.
【范例2】设函数 .
.
(Ⅰ)求 的最小值
的最小值 ;
;
(Ⅱ)若 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
解:(Ⅰ) ,
,
 当
当 时,
时, 取最小值
取最小值 ,
,
即 .
.
(Ⅱ)令 ,
,
由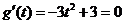 得
得 ,
, (不合题意,舍去).
(不合题意,舍去).
当 变化时
变化时 ,
, 的变化情况如下表:
的变化情况如下表:

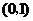







递增
极大值
递减
 在
在 内有最大值
内有最大值 .
.
 在
在 内恒成立等价于
内恒成立等价于 在
在 内恒成立,
内恒成立,
即等价于 ,
,
所以 的取值范围为
的取值范围为 .
.
变式:函数f(x)是奇函数,且在[―l,1]上单调递增,f(-1)=-1,(1) 则f(x)在[-1,1]上的最大值 1
,(2) 若 对所有的x∈[-1,1]及a∈[-1,1]都成立,则t的取值范围是
对所有的x∈[-1,1]及a∈[-1,1]都成立,则t的取值范围是  _ .
_ .
【范例3】已知函数 与
与 的图象相交于
的图象相交于 ,
, ,
, ,
, 分别是
分别是 的图象在
的图象在 两点的切线,
两点的切线, 分别是
分别是 ,
, 与
与 轴的交点.
轴的交点.
(I)求 的取值范围;
的取值范围;
(II)设 为点
为点 的横坐标,当
的横坐标,当 时,写出
时,写出 以
以 为自变量的函数式,并求其定义域和值域;
为自变量的函数式,并求其定义域和值域;
(III)试比较 与
与 的大小,并说明理由(
的大小,并说明理由( 是坐标原点).
是坐标原点).
解:(I)由方程 消
消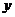 得
得 .????? ①
.????? ①
依题意,该方程有两个正实根,
故 解得
解得 .
.
(II)由 ,求得切线
,求得切线 的方程为
的方程为 ,
,
由 ,并令
,并令 ,得
,得
 ,
, 是方程①的两实根,且
是方程①的两实根,且 ,故
,故 ,
, ,
,
 是关于
是关于 的减函数,所以
的减函数,所以 的取值范围是
的取值范围是 .
.
 是关于
是关于 的增函数,定义域为
的增函数,定义域为 ,所以值域为
,所以值域为 ,
,
(III)当 时,由(II)可知
时,由(II)可知 .
.
类似可得 .
. .
.
由①可知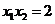 .
.
从而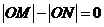 .
.
当 时,有相同的结果
时,有相同的结果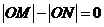 .
.
所以 .
.
变式:已知函数
 的最大值是
的最大值是 ,最小值是
,最小值是 ,求
,求 的值。
的值。
分析提示:(1)能化成关于 的二次函数,注意对数的运算法则;(2)注意挖掘隐含条件“
的二次函数,注意对数的运算法则;(2)注意挖掘隐含条件“ ”;(3)掌握复合函数最值问题的求解方法。
”;(3)掌握复合函数最值问题的求解方法。
解:

= , ∵
, ∵ ,且
,且
∴当 即
即 时,
时,
∴ ∴
∴ ,又
,又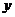 最大值是
最大值是 ,,
,,
∴ 即
即 , ∴
, ∴ 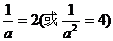 ∴
∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com