
第二十三讲 空间位置关系与证明
★★★高考在考什么
【考题回放】
 1.(浙江)若
1.(浙江)若 是两条异面直线
是两条异面直线 外的任意一点,则(B )
外的任意一点,则(B )
A.过点 有且仅有一条直线与
有且仅有一条直线与 都平行
都平行
B.过点 有且仅有一条直线与
有且仅有一条直线与 都垂直
都垂直
C.过点 有且仅有一条直线与
有且仅有一条直线与 都相交
都相交
D.过点 有且仅有一条直线与
有且仅有一条直线与 都异面
都异面
2.(06湖南)如图,过平行六面体ABCD-A1B1C1D1任意两条棱的中
点作直线,其中与平面DBB1D1平行的直线共有( D )
A.4条 B.6条 C.8条 D.12条
3.(湖北)平面 外有两条直线
外有两条直线 和
和 ,如果
,如果 和
和 在平面
在平面 内的射影分别是
内的射影分别是 和
和 ,给出下列四个命题:
,给出下列四个命题:
① ;
;
② ;
;
③ 与
与 相交
相交
 与
与 相交或重合;
相交或重合;
④ 与
与 平行
平行
 与
与 平行或重合.
平行或重合.
其中不正确的命题个数是( D )
A.1 B.2 C.3 D.4
4.(湖北)关于直线 、
、 与平面
与平面 、
、 ,有下列四个命题:(D )
,有下列四个命题:(D )
① 且
且 ,则
,则 ; ②
; ② 且
且 ,则
,则 ;
;
③ 且
且 ,则
,则 ; ④
; ④ 且
且 ,则
,则 .
.
其中真命题的序号是:
A. ①、② B. ③、④ C. ①、④ D. ②、③
5.在正方形 中,过对角线
中,过对角线 的一个平面交
的一个平面交 于E,交
于E,交 于F,则( )
于F,则( )
①
四边形 一定是平行四边形
一定是平行四边形
②
四边形 有可能是正方形
有可能是正方形
③
四边形 在底面ABCD内的投影一定是正方形
在底面ABCD内的投影一定是正方形
④
四边形 有可能垂直于平面
有可能垂直于平面
以上结论正确的为 ①③④ 。(写出所有正确结论的编号)
6.(上海)在平面上,两条直线的位置关系有相交、平行、重合三种.
已知 是两个相交平面,空间两条直线
是两个相交平面,空间两条直线 在
在 上的射影是直线
上的射影是直线 ,
, 在
在 上的射影是直线
上的射影是直线 .用
.用 与
与 ,
, 与
与 的位置关系,写出一个总能确定
的位置关系,写出一个总能确定 与
与 是异
是异
面直线的充分条件:
 ,并且
,并且 与
与 相交(
相交(
 ,并且
,并且 与
与 相交)
相交)
★ ★★高考要考什么
一.线与线的位置关系:平行、相交、异面;
 ;
;
★★★高考将考什么
【范例1】如图,在四棱锥 中,
中, 底面
底面 ,
, ,
, ,
, 是
是 的中点.
的中点.
 (Ⅰ)证明
(Ⅰ)证明 ;
;
(Ⅱ)证明 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
(Ⅰ)证明:在四棱锥 中,
中,
因 底面
底面 ,
, 平面
平面 ,故
,故 .
.
 ,
, 平面
平面 .
.
而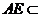 平面
平面 ,
, .
.
(Ⅱ)证明:由 ,
,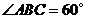 ,可得
,可得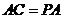 .
.
 是
是 的中点,
的中点, .
.
由(Ⅰ)知, ,且
,且 ,所以
,所以 平面
平面 .
.
而 平面
平面 ,
, .
.
 底面
底面 在底面
在底面 内的射影是
内的射影是 ,
, ,
, .
.
又 ,综上得
,综上得 平面
平面 .
.
(Ⅲ)解法一:过点 作
作 ,垂足为
,垂足为 ,连结
,连结 .则(Ⅱ)知,
.则(Ⅱ)知, 平面
平面 ,
, 在平面
在平面 内的射影是
内的射影是 ,则
,则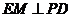 .
.
因此 是二面角
是二面角 的平面角.
的平面角.
由已知,得 .设
.设 ,
,
 可得
可得 .
.
在 中,
中, ,
, ,
,
则 .
.
在 中,
中, .
.
解法二:由题设 底面
底面 ,
, 平面
平面 ,则平面
,则平面 平面
平面 ,交线为
,交线为 .
.
 过点
过点 作
作 ,垂足为
,垂足为 ,故
,故 平面
平面 .过点
.过点 作
作 ,垂足为
,垂足为 ,连结
,连结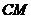 ,故
,故 .因此
.因此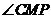 是二面角
是二面角 的平面角.
的平面角.
由已知,可得 ,设
,设 ,
,
可得 .
.
 ,
,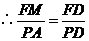 .
.
于是, .
.
在 中,
中, .
.
所以二面角 的大小是
的大小是 .
.
所以二面角 的大小是
的大小是 .
.
 变式:如图,在五面体
变式:如图,在五面体 中,点
中,点 是矩形
是矩形 的对角线的交点,面
的对角线的交点,面 是等边三角形,棱
是等边三角形,棱 .
.
(1)证明 //平面
//平面 ;
;
(2)设 ,证明
,证明 平面
平面 .
.
证明:(Ⅰ)取CD中点M,连结OM.
在矩形ABCD中, ,又
,又 ,则
,则 ,
,
连结EM,于是四边形EFOM为平行四边形. 
又 平面CDE, EM
平面CDE, EM 平面CDE, ∴ FO∥平面CDE
平面CDE, ∴ FO∥平面CDE
(Ⅱ)证明:连结FM,由(Ⅰ)和已知条件,在等边△CDE中,
 且
且 .
.
因此平行四边形EFOM为菱形,从而EO⊥FM而FM∩CD=M,
∴CD⊥平面EOM,从而CD⊥EO. 而 ,所以EO⊥平面CDF.
,所以EO⊥平面CDF.
 【点晴】本小题考查直线与平面平行、直线与平面垂直等基础知识,注意线面平行和线面垂直判定定理的使用,考查空间想象能力和推理论证能力。
【点晴】本小题考查直线与平面平行、直线与平面垂直等基础知识,注意线面平行和线面垂直判定定理的使用,考查空间想象能力和推理论证能力。
【范例2】如图,在六面体 中,四边形
中,四边形 是边长为2的正方形,四边形
是边长为2的正方形,四边形 是边长为1的正方形,
是边长为1的正方形, 平面
平面
 ,
, 平面
平面 ,
, .
.
(Ⅰ)求证: 与
与 共面,
共面, 与
与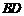 共面.
共面.
(Ⅱ)求证:平面 平面
平面 ;
;
(Ⅲ)求二面角 的大小(用反三角函数值表示).
的大小(用反三角函数值表示).
证明:以 为原点,以
为原点,以 所在直线分别为
所在直线分别为 轴,
轴,
 轴,
轴, 轴建立空间直角坐标系
轴建立空间直角坐标系 如图,
如图,
则有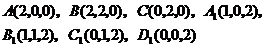 .
.
(Ⅰ)证明:
 .
.

 .
.
 与
与 平行,
平行, 与
与 平行,
平行,
于是 与
与 共面,
共面, 与
与 共面.
共面.
(Ⅱ)证明: ,
,
 ,
,
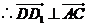 ,
, .
.
 与
与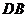 是平面
是平面 内的两条相交直线.
内的两条相交直线.
 平面
平面 .
.
又平面 过
过 .
.
 平面
平面 平面
平面 .
.
(Ⅲ)解: .
.
设 为平面
为平面 的法向量,
的法向量,
 ,
, .
.
于是 ,取
,取 ,则
,则 ,
, .
.
设 为平面
为平面 的法向量,
的法向量,
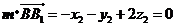 ,
, .
.
于是 ,取
,取 ,则
,则 ,
, .
.
 .
.
 二面角
二面角 的大小为
的大小为 .
.
解法2(综合法):
(Ⅰ)证明: 平面
平面 ,
, 平面
平面 .
.
 ,
, ,平面
,平面 平面
平面 .
.
于是 ,
, .
.
 设
设 分别为
分别为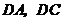 的中点,连结
的中点,连结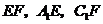 ,
,
有 .
.
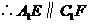 ,
,
于是 .
.
由 ,得
,得 ,
,
故 ,
, 与
与 共面.
共面.
过点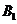 作
作 平面
平面 于点
于点 ,
,
则 ,连结
,连结 ,
,
于是 ,
, ,
,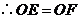 .
.
 ,
, .
.
 ,
, .
.
所以点 在
在 上,故
上,故 与
与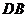 共面.
共面.
(Ⅱ)证明: 平面
平面 ,
, ,
,
又 (正方形的对角线互相垂直),
(正方形的对角线互相垂直),
 与
与 是平面
是平面 内的两条相交直线,
内的两条相交直线,
 平面
平面 .
.
又平面 过
过 ,
, 平面
平面 平面
平面 .
.
(Ⅲ)解: 直线
直线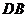 是直线
是直线 在平面
在平面 上的射影,
上的射影, ,
,
根据三垂线定理,有 .
.
过点 在平面
在平面 内作
内作 于
于 ,连结
,连结 ,
,
则 平面
平面 ,
,
于是 ,
,
所以, 是二面角
是二面角 的一个平面角.
的一个平面角.
根据勾股定理,有 .
.
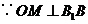 ,有
,有 ,
,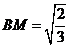 ,
, ,
, .
.
 ,
, ,
,
二面角 的大小为
的大小为 .
.
 变式如图,已知
变式如图,已知 是棱长为
是棱长为 的正方体,
的正方体,
点 在
在 上,点
上,点 在
在 上,且
上,且 .
.
(1)求证: 四点共面;(4分)
四点共面;(4分)
(2)若点 在
在 上,
上, ,点
,点 在
在 上,
上,
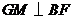 ,垂足为
,垂足为 ,求证:
,求证: 平面
平面 ;(4分)
;(4分)
(3)用 表示截面
表示截面 和侧面
和侧面 所成的锐二面角的大小,求
所成的锐二面角的大小,求 .
.
 证明:(1)建立如图所示的坐标系,则
证明:(1)建立如图所示的坐标系,则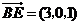 ,
,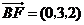 ,
, ,
,
所以 ,故
,故 ,
, ,
, 共面.
共面.
又它们有公共点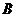 ,所以
,所以 四点共面.
四点共面.
(2)如图,设 ,则
,则 ,
,
而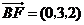 ,由题设得
,由题设得 ,
,
得 .
.
因为 ,
, ,有
,有 ,又
,又 ,
, ,所以
,所以 ,
, ,从而
,从而 ,
, .
.
故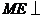 平面
平面 .
.
(3)设向量 截面
截面 ,于是
,于是 ,
, .
.
而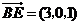 ,
,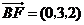 ,得
,得 ,
, ,解得
,解得 ,
, ,所以
,所以 .
.
又 平面
平面 ,所以
,所以 和
和 的夹角等于
的夹角等于 或
或 (
( 为锐角).
为锐角).
于是 .
.
故 .
.
 【范例3】如图,在长方体AC1中,AD=AA1=1,AB=2,点E在棱AB上移动.
【范例3】如图,在长方体AC1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1―EC―D的大小为 .
.
解析:法1
(1)∵AE⊥面AA1DD1,A1D⊥AD1,∴A1D⊥D1E
(2)设点E到面ACD1的距离为h,在△ACD1中,AC=CD1= ,AD1=
,AD1= ,
,
故

 (3)过D作DH⊥CE于H,连D1H、DE,则D1H⊥CE,
(3)过D作DH⊥CE于H,连D1H、DE,则D1H⊥CE,
∴∠DHD1为二面角D1―EC―D的平面角.
设AE=x,则BE=2-x
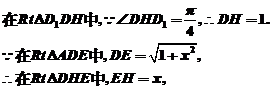

法2:以D为坐标原点,直线DA、DC、DD1分别为x、y、z轴,建立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A(1,0,0), C(0,2,0).
 (1)
(1)
(2)因为E为AB的中点,则E(1,1,0),
从而 ,
, ,
,
设平面ACD1的法向量为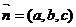 ,
,
则 也即
也即 ,得
,得 ,
,
从而 ,所以点E到平面AD
,所以点E到平面AD
(3)设平面D1EC的法向量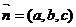 ,
,
∴
由 令b=1, ∴c=2, a=2-x,
令b=1, ∴c=2, a=2-x,
∴ 依题意
依题意
∴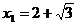 (不合,舍去),
(不合,舍去), .
.
∴AE= 时,二面角D1―EC―D的大小为
时,二面角D1―EC―D的大小为 .
.
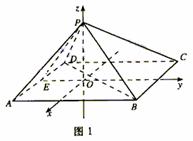
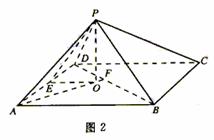 变式:如图,四棱锥P―ABCD中,底面ABCD 为矩形,AB=8,AD=4
变式:如图,四棱锥P―ABCD中,底面ABCD 为矩形,AB=8,AD=4 ,侧面PAD为等边三角形,并且与底面所成二面角为60°.
,侧面PAD为等边三角形,并且与底面所成二面角为60°.
(Ⅰ)求四棱锥P―ABCD的体积;
(Ⅱ)证明PA⊥BD.
解析:(Ⅰ)如图,取AD的中点E,
连结PE,则PE⊥AD.
作PO⊥平面在ABCD,垂足为O,连结OE.
根据三垂线定理的逆定理得OE⊥AD,
所以∠PEO为侧面PAD与底面所成的二面角
的平面角,由已知条件可知∠PEO=60°,PE=6,所以PO=3 ,
,
四棱锥P―ABCD的体积VP―ABCD=
(Ⅱ)法1 如图,以O为原点建立空间直角坐标系.通过计算可得P(0,0,3 ),
),
 A(2
A(2 ,-3,0),B(2
,-3,0),B(2 ,5,0),D(-2
,5,0),D(-2 ,-3,0)
,-3,0)
所以
因为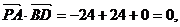 所以PA⊥BD.
所以PA⊥BD.
法2:连结AO,延长AO交BD于点F.通过计算
可得EO=3,AE=2 ,又知AD=4
,又知AD=4 ,AB=8,
,AB=8,
得 所以Rt△AEO∽Rt△BAD.得∠EAO=∠ABD.
所以Rt△AEO∽Rt△BAD.得∠EAO=∠ABD.
所以∠EAO+∠ADF=90° 所以 AF⊥BD.
因为 直线AF为直线PA在平面ABCD 内的身影,所以PA⊥BD.
【点晴】本小题主要考查棱锥的体积、二面角、异面直线所成的角等知识和空间想象能力、分析问题能力,解题的关键是二面角的使用。使用空间向量能降低对空间想象能力的要求,但坐标系的位置不规则,注意点坐标的表示。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com