例1. 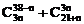的值是_________________。

解：从组合数定义有：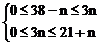

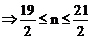
又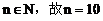  ，代入再求，得出466。

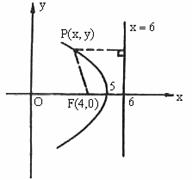例2. 到椭圆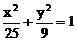右焦点的距离与到定直线x＝6距离相等的动点的轨迹方_______________。

解：据抛物线定义，结合图知：

轨迹是以（5，0）为顶点，焦参数P＝2且开口方向向左的抛物线，故其方程为：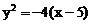

（二）直接法

这是解填空题的基本方法，它是直接从题设条件出发、利用定理、性质、公式等知识，通过变形、推理、运算等过程，直接得到结果。

例3设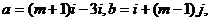其中i，j为互相垂直的单位向量，又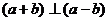，则实数m =              。

解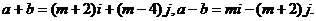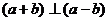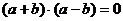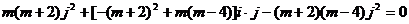：∵，∴∴，而i，j为互相垂直的单位向量，故可得∴。

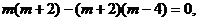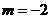例4已知函数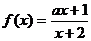在区间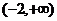上为增函数，则实数a的取值范围是      。

解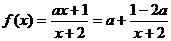：，由复合函数的增减性可知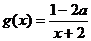，在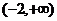上为增函数，∴，∴。

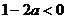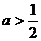例5现时盛行的足球彩票，其规则如下：全部13场足球比赛，每场比赛有3种结果：胜、平、负，13长比赛全部猜中的为特等奖，仅猜中12场为一等奖，其它不设奖，则某人获得特等奖的概率为         。

解：由题设，此人猜中某一场的概率为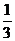，且猜中每场比赛结果的事件为相互独立事件，故某人全部猜中即获得特等奖的概率为。

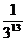（三）特殊化法

当填空题的结论唯一或题设条件中提供的信息暗示答案是一个定值时，可以把题中变化的不定量用特殊值代替，即可以得到正确结果。

例6 在△ABC中，角A、B、C所对的边分别为a、b、c。若a、b、c成等差数列，则             。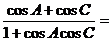

解：特殊化：令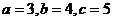，则△ABC为直角三角形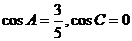，，从而所求值为。

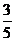例7 过抛物线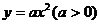的焦点F作一直线交抛物线交于P、Q两点，若线段PF、FQ的长分别为p、q，则           。

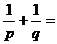分析：此抛物线开口向上，过焦点且斜率为k的直线与抛物线均有两个交点P、Q，当k变化时PF、FQ的长均变化，但从题设可以得到这样的信息：尽管PF、FQ不定，但其倒数和应为定值，所以可以针对直线的某一特定位置进行求解，而不失一般性。

解：设k = 0，因抛物线焦点坐标为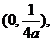把直线方程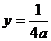代入抛物线方程得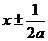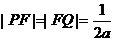，∴，从而。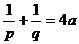

例8  求值         。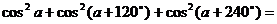

分析：题目中“求值”二字提供了这样信息：答案为一定值，于是不妨令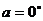，得结果为。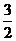

例9如果函数f(x)=x²+bx+c对任意实数t都有f(2+t)=f(2-t)，那么f(1),f(2),f(4)的大小关系是 

解：  由于f(2+t)=f(2-t)，故知f(x)的对称轴是x=2。可取特殊函数f(x)=(x-2)²,即可求得f(1)=1,f(2)=0,f(4)=4。∴f(2)<f(1)<f(4)。

 例10已知等差数列{a_n}的公差d≠0，且a₁,a₃,a₉成等比数列，则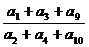的值是          。

解：  考虑到a₁,a₃,a₉的下标成等比数列，故可令a_n=n满足题设条件，于是=。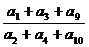

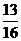例11椭圆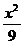+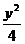=1的焦点为F₁、F₂，点P为其上的动点，当∠F₁PF₂为钝角时，点P横坐标的取值范围是               。

解：  设P(x,y)，则当∠F₁PF₂=90°时，点P的轨迹方程为x²+y²=5，由此可得点P的横坐标x=±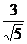，又当点P在x轴上时，∠F₁PF₂=0；点P在y轴上时，∠F₁PF₂为钝角，由此可得点P横坐标的取值范围是-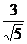<x<。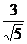

（四）数形结合法

对于一些含有几何背景的填空题，若能数中思形，以形助数，则往往可以简捷地解决问题，得出正确的结果。

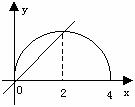
例12   如果不等式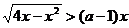的解集为A，且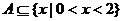，那么实数a的取值范围是          。

解：根据不等式解集的几何意义，作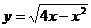函数和函数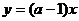的图象（如图），从图上容易得出实数a的取值范围是。

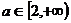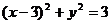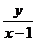例13  已知实数x、y满足，则的最大值是         。

解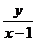：可看作是过点P（x，y）与M（1，0）的直线的斜率，其中点P的圆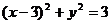上，如图，当直线处于图中切线位置时，斜率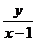最大，最大值为。

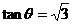（五）等价转化法

通过“化复杂为简单、化陌生为熟悉”，将问题等价地转化成便于解决的问题，从而得出正确的结果。

例14  不等式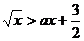的解集为（4，b），则a=           ，b=          。

解：设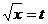，则原不等式可转化为：∴a > 0，且2与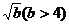是方程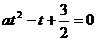的两根，由此可得：。

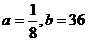例15  不论k为何实数，直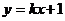线与曲线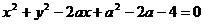恒有交点，则实数a的取值范围是        。

解：题设条件等价于点（0，1）在圆内或圆上，或等价于点（0，1）到圆，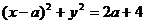

∴。

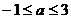例16  函数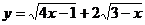单调递减区间为             。

解：易知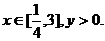∵y与y²有相同的单调区间，而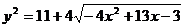，∴可得结果为。

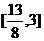    总之，能够多角度思考问题，灵活选择方法，是快速准确地解数学填空题的关键。

（六） 淘汰法

当全部情况为有限种时，也可采用淘汰法。

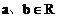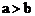例17. 已知，则与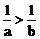同时成立的充要条件是____________。

解：按实数b的正、负分类讨论。

当b>0时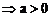，而等式不可能同时成立；

当b＝0时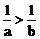，无意义；

当b<0时，若a<0，则两不等式不可能同时成立，以上三种情况均被淘汰，故只能为a>0，b<0，容易验证，这确是所要求的充要条件。