|
试题详情
B. 试题详情
C.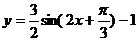 试题详情
D. 试题详情
6.在某次数学测验中,学号 的四位同学的考试成绩 的四位同学的考试成绩 ,且满足 ,且满足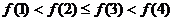 ,则四位同学的考试成绩的所有情况的种数为( ) ,则四位同学的考试成绩的所有情况的种数为( ) A.9种 B.5种
C.23种
D.15种 试题详情
试题详情
试题详情
试题详情
试题详情
二、填空题(共7 题,每小题5分,共同社35分) 9.在等差数列 的值是 的值是
试题详情
试题详情
试题详情
则 。
。 试题详情
试题详情
13.一个总体共有100个个体,随机编号0,1,2,…,99,按从小到大的编号顺序平均分成10个小组,组号依次为1,2,3,…,10,现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同,若m=4,则在第6组中抽取的号码是
试题详情
14.用4种不同的颜色为正方体A 的六个面着色,要求相邻两个面颜色不相同,则不同的着色方法种数有 的六个面着色,要求相邻两个面颜色不相同,则不同的着色方法种数有
试题详情
15.甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头(假设无其它船驶向该码头),它们在一昼夜内任何时刻到达是等可能的.如果甲船和乙船的停泊时间都是4小时,则它们中的任何一条船不需要等等码头空出的概率为
16(本小题满分12分) 试题详情
三、解答题(共6小题,共75分,解答应写出文字说明,证明过程或演算过程) 向量a=(sinωx+cosωx,1),b=(f(x),simωx),其中0<ω<l,且a∥b.将f(x)的图象沿x轴向左平移 个单位,沿y轴向下平移 个单位,沿y轴向下平移 个单位,得到g(x)的图象,已知g(x)的图象关于( 个单位,得到g(x)的图象,已知g(x)的图象关于( ,0)对称 ,0)对称 (1)求ω的值; (2)求g(x)在[0,4π]上的单调递增区间. 17(本小题满分12分) 试题详情
 正四棱柱ABCD―A1B1C1D1中,已知AB=2,E,F分别是D1B,AD的中点,cos 正四棱柱ABCD―A1B1C1D1中,已知AB=2,E,F分别是D1B,AD的中点,cos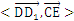 = =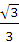 . .
(1)建立适当的坐标系,求出E点的坐标; (2)证明:EF是异面直线D1B与AD的公垂线; (3)求二面角D1―BF―C的余弦值. 18(本小题满分12分) 某机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利总额为y万元. (1)写出y与x之间的函数关系式; (2)从第几年开始,该机床开始盈利(盈利额为正值) (3)使用若干年后,对机床的处理方案有两种:(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床. 请你研究一下哪种方案处理较为合理?请说明理由. 19(本小题满分12分) 试题详情
试题详情
(1)当直线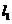 的倾斜角为 的倾斜角为 ,双曲线的焦距为8时,求椭圆的方程; ,双曲线的焦距为8时,求椭圆的方程; 试题详情
 (2)设 (2)设 ,证明: ,证明: 为常数. 为常数.
20(本小题满分13分) 甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约。甲表示只要面 试题详情
试合格就签约;乙、丙则约定:如果两人面试都合格就一同签约,否则两人都不签约。设甲面试合格的概率为 ,乙、丙面试合格的概率都是 ,乙、丙面试合格的概率都是 ,且面试是否合格互不影响.求: ,且面试是否合格互不影响.求: (1)至少有1人面试合格的概率; 试题详情
(2)签约人数 的分布列和数学期望. 的分布列和数学期望. 21(本小题满分14分) 试题详情
试题详情
试题详情
试题详情
试题详情
②当 时,求证: 时,求证:
试题详情
一、
BCCC,ADBA 二、
30 2 1 1  50 96 96 50 96 96 三、
解答题 16 (1)   ω (2)  17
(I)以D为原点,DA,DC,DD1所在直线为x轴,y轴,z轴,建立系 E点坐标为(1,1,1). (2) 略 (3)二面角D1―BF―C的余弦值为 18 (1)  (2)  (3)(Ⅰ) 当且仅当 时,即x=7时等号成立. 时,即x=7时等号成立.  到第7年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.……10分 到第7年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.……10分 (Ⅱ) 故到第10年,盈利额达到最大值,工厂获利102+12=114万元
……11分 盈利额达到的最大值相同,而方案Ⅰ所用的时间较短,故方案Ⅰ比较合理.…12分 19(1)椭圆 的方程是: 的方程是: . . (2) , , , ,
 为常数. 为常数. 20 (1)用A,B,C分别表示事件甲、乙、丙面试合格.由题意知A,B,C相互独立, 至少有1人面试合格的概率是 (2)∴ 的分布列是 的分布列是 
0 1 2 3 




 的期望 的期望
21(1) (2)(2)① (2)(2)①   , , . . 当 当 时, 时, . 假设 . 假设 ,则 ,则 . . 由数学归纳法证明 为常数数列,是等差数列,其通项为 为常数数列,是等差数列,其通项为 . ……8分 . ……8分 ② , ,  . .  当 当 时, 时, . 假设 . 假设 ,则 ,则
 . .
由数学归纳法,得出数列  .……………10分 .……………10分 又 , , , , 即 ………12分 ………12分     . .
 , , . ………………14分 . ………………14分
| 
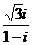 的共轭复数是
( )
的共轭复数是
( ) B.
B. C.
C. D.
D.
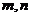 是两条不同的直线,
是两条不同的直线, 是两个不重合的平面,
是两个不重合的平面, ,则
,则 的
( )
的
( ) B.
B. C.
C. D.
D.
 ,且
,且 ,则
,则 ( )
( ) B.
B. C.
C. 或
或 D.
D.  或
或
 的图象如下,则y的表达式是 ( )
的图象如下,则y的表达式是 ( )