|
试题详情
A. B. B.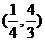 试题详情
C. D. D.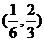 试题详情
12.某公司有60万元资金,计划投资甲、乙两个项目,按要求对项目甲的投资不小于对项目乙投资的 倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确规划投资后,在这两个项目上共可获得的最大利润为 ( ) 倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确规划投资后,在这两个项目上共可获得的最大利润为 ( ) 试题详情
A.36万元 B.31.2万元 C.30.4万元 D.24万元 试题详情
二、填空题:(本大题共4个小题,每小题4分,共16分。请把答案填在答题纸的相应位置上) 13.设集合 = 。 = 。 试题详情
14.若 的终边所在直线方程为
。 的终边所在直线方程为
。 试题详情
15.设O是△ABC内部一点,且 则△AOB与△AOC面积之比是 。 则△AOB与△AOC面积之比是 。 试题详情
试题详情
三、解答题:本大题共6小题,满分74分。解答应写出必要的文字说明、证明过程或演算步骤。请将解答过程写在答题纸的相应位置。
试题详情
已知向量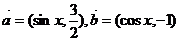 试题详情
(I)当 的值; 的值; 试题详情
(II)求 上的值域。 上的值域。 试题详情
18.(本小题满分12分) 某观测站C在城A的南偏西20°的方向上,由A城出发有一条公路,走向是南偏东40°,在C处测得距C为31千米的公路上B处有一人正沿公路向A城走去,走了20千米后,到达D处,此时C、D间距离为21千米,问这人还需要走多少千米到达A城? 试题详情
试题详情
已知⊙O: 和定义A(2,1),由⊙O外一点P(a,b)向⊙O引切线PQ,切点Q,且满足|PQ|=|PA|。 和定义A(2,1),由⊙O外一点P(a,b)向⊙O引切线PQ,切点Q,且满足|PQ|=|PA|。 (1)求实数a、b间满足的等量关系; (2)求线段PQ长的最小值; (3)若以P为圆心所作的⊙P与⊙Q有公共点,试求半径取最小值时,⊙P的方程。 试题详情
20.(本小题满分12分) 如图,四棱锥P―ABCD,底面ABCD是矩形,PA⊥平面ABCD,PA=AD,点E、F分别是AB、PC的中点。 (I)求证:EF//平面PAD; (II)求证:平面PEC⊥平面PCD。 试题详情
|
|
|
试题详情
试题详情
已知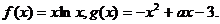 试题详情
(I)求函数 上的最小值; 上的最小值; 试题详情
(II)对一切 的取值范围; 的取值范围; 试题详情
试题详情
在数列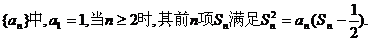 试题详情
(I)求 ; ; 试题详情
(II)设 ; ; 试题详情
(III)是否存在自然数m,使得对任意 成立?若存在,求出m的最大值;若不存在,请说明理由。 成立?若存在,求出m的最大值;若不存在,请说明理由。 试题详情
一、选择题:本大题共12个小题,每小题5分,共60分。 1―5 BCBAB 6―10 DCCCD 11―12 DB 二、填空题:本大题共4个小题,每小题4分,共16分。 13. 14. 14. 15.1:2 16.①②⑤ 15.1:2 16.①②⑤
20090203 17.(本小题满分12分) 解:(I) 共线 共线   ………………3分 ………………3分 故 …………6分 …………6分 (II)   …………12分 …………12分 18.(本小题满分12分) 解:根据题意得图02,其中BC=31千米,BD=20千米,CD=21千米, ∠CAB=60˚.设∠ACD = α ,∠CDB = β .

 , ,
 . .


 .……9分 .……9分
在△ACD中,由正弦定理得:  . .

19.(本小题满分12分) 解:(1)连结OP,∵Q为切点,PQ OQ, OQ, 由勾股定理有, 又由已知 即: 化简得 …………3分 …………3分 (2)由 ,得 ,得  …………6分 …………6分
故当 时, 时, 线段PQ长取最小值 线段PQ长取最小值 …………7分 …………7分 (3)设⊙P的半径为R,∵⊙P与⊙O有公共点,⊙O的半径为1, ∴ 即R 即R 且R 且R 而 故当 时, 时, ,此时b=―2a+3= ,此时b=―2a+3= 得半径最最小值时⊙P的方程为 …………12分 …………12分 20.(本小题满分12分) 解:(I)取PD的中点G,连结FG、AG,则

又E为AB的中点 
∴四边形AEFG为平行四边形 …………3分 ∴EF∥AG 又AG 平面PAD 平面PAD ∴EF∥平面PAD …………5分
(II)∵PA⊥平面ABCD ∴PA⊥AE 又矩形ABCD中AE⊥AD ∴AE⊥平面PAD ∴AE⊥AG ∴AE⊥EF 又AE//CD ∴ED⊥CD …………8分 又∵PA=AD ∴在Rt△PAE和Rt△CBE中PE=CE ∵D为PC的中点 ∴EF⊥PC …………10分 又PC∩CD=C ∴EF⊥平面PCD 又EF 平面PEC 平面PEC ∴平面PEC⊥平面PCD …………12分 22.(本小题满分12分) 解:(I)  单调递增。 …………2分 单调递增。 …………2分
① ,不等式无解; ,不等式无解; ② ; ; ③ ; ; 所以 …………6分 …………6分
(II) , …………8分 , …………8分 
……………11分 因为对一切 ……12分 ……12分 22.(本小题满分14分) 解:(I) 
(II) …………7分 …………7分 
(III)令 上是增函数 上是增函数 

| | | | | | | | | | | 
 高三年级期末测试
高三年级期末测试 等于 ( )
等于 ( ) D.
D.
 下列结论中正确的是 ( )
下列结论中正确的是 ( ) ”是真命题 B.命题“
”是真命题 B.命题“ ”是真命题
”是真命题 ”是真命题 D.命题“
”是真命题 D.命题“ ”是假命题
”是假命题 = ( )
= ( ) 处的切线方程为 ( )
处的切线方程为 ( ) B.
B. C.
C. D.
D.