
2004年湖南省高中数学竞赛试题
一、选择题:(本大题共10个小题;每小题5分,共50分,在每小题给出的四个选项中, 有且只有一项是符合题目要求的)
1.已知函数f(x)是R上的奇函数,g(x)是R上的偶函数,若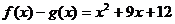 ,则
,则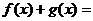 ( )
( )
A.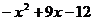 B.
B.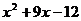 C.
C.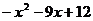 D.
D. 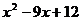
2.有四个函数:① y=sinx+cosx ② y=
sinx-cosx
③ y=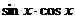 ④
④ 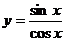
其中在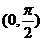 上为单调增函数的是 ( )
上为单调增函数的是 ( )
A.① B.② C.①和③ D.②和④
3.方程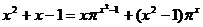 的解集为A(其中π为无理数,π=3.141…,x为实数),则A中所有元素的平方和等于 ( )
的解集为A(其中π为无理数,π=3.141…,x为实数),则A中所有元素的平方和等于 ( )
A.0 B.1 C.2 D.4
4.已知点P(x,y)满足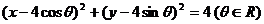 ,则点P(x,y)所在区域的面积为
,则点P(x,y)所在区域的面积为
A.36π B.32π C.20π D.16π ( )
5.将10个相同的小球装入3个编号为1、2、3的盒子(每次要把10个球装完),要求每个盒子里球的个数不少于盒子的编号数,这样的装法种数为 ( )
A.9 B.12 C.15 D.18
6.已知数列{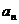 }为等差数列,且S5=28,S10=36,则S15等于 ( )
}为等差数列,且S5=28,S10=36,则S15等于 ( )
A.80 B.40 C.24 D.-48
7.已知曲线C: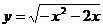 与直线
与直线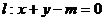 有两个交点,则m的取值范围是 ( )
有两个交点,则m的取值范围是 ( )
A.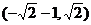 B.
B.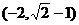 C.
C.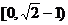 D.
D.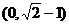
8.过正方体ABCD-A1B1C1D1的对角线BD1的截面面积为S,Smax和Smin分别为S的最大值和最小值,则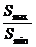 的值为 ( )
的值为 ( )
A.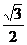 B.
B.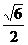 C.
C.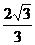 D.
D.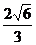
9.设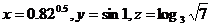 ,则x、y、z的大小关系为 ( )
,则x、y、z的大小关系为 ( )
A.x<y<z B.y<z<x C.z<x<y D. z<y<x
10.如果一元二次方程 中,a、b分别是投掷骰子所得的数字,则该二次方程有两个正根的概率P= ( )
中,a、b分别是投掷骰子所得的数字,则该二次方程有两个正根的概率P= ( )
A.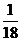 B.
B. C.
C.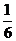 D.
D.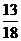
二、填空题(本大题共4个小题,每小题8分,共32分)
11.设P是椭圆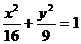 上异于长轴端点的任意一点,F1、F2分别是其左、右焦点,O为中心,则
上异于长轴端点的任意一点,F1、F2分别是其左、右焦点,O为中心,则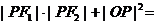 ___________.
___________.
12.已知△ABC中,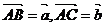 ,试用
,试用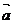 、
、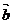 的向量运算式子表示△ABC的面积,即S△ABC=
的向量运算式子表示△ABC的面积,即S△ABC=
____________________.
13.从3名男生和n名女生中,任选3人参加比赛,已知3人中至少有1名女生的概率为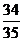 ,则n=__________.
,则n=__________.
14.有10名乒乓球选手进行单循环赛,比赛结果显示,没有和局,且任意5人中既有1人胜其余4人,又有1人负其余4人,则恰好胜了两场的人数为____________个.
三、解答题(本大题共5个小题,15-17题每小题12分,18题、19题每小题16分,共68分)
15.对于函数f(x),若f(x)=x,则称x为f(x)的“不动点”,若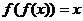 ,则称x为f(x)的“稳定点”,函数f(x)的“不动点”和“稳定点”的集合分别记为A和B,即
,则称x为f(x)的“稳定点”,函数f(x)的“不动点”和“稳定点”的集合分别记为A和B,即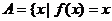 }
}
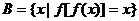 .
.
(1). 求证:A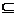 B
B
(2).若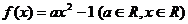 ,且
,且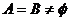 ,求实数a的取值范围.
,求实数a的取值范围.
16.某制衣车间有A、B、C、D共4个组,各组每天生产上衣或裤子的能力如下表,现在上衣及裤子要配套生产(一件上衣及一条裤子为一套),问在7天内,这4个组最多能生产多少套?
组
A
B
C
D
上衣(件)
8
9
7
6
裤子(条)
10
12
11
7
17.设数列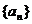 满足条件:
满足条件: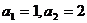 ,且
,且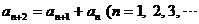 )
)
求证:对于任何正整数n,都有
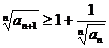
18.在周长为定值的△ABC中,已知|AB|=6,且当顶点C位于定点P时,cosC有最小值为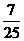 .
.
(1).建立适当的坐标系,求顶点C的轨迹方程.
(2).过点A作直线与(1)中的曲线交于M、N两点,求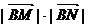 的最小值的集合.
的最小值的集合.
19.已知三棱锥O-ABC的三条侧棱OA、OB、OC两两垂直,P是底面△ABC内的任一点,OP与三侧面所成的角分别为α、β、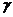 .
.
求证:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com