2005年青岛市学业水平考试统一质量检测数学试题
（考试时间：120分钟 满分：120分）
一. 选择题（本题满分18分，共有6道小题，每小题3分）
1. 如图，圆周角
的度数为
，则圆心角
的度数为（ ）
A. B. 
C. 
D. 
2. 下列运算正确的是（ ）
A. 
B. 
C. 
D. 
3. 下列图形中，不可能围成正方体的有（ ）个
A. 1 B. 2 C. 3 D. 4
4. 把标有号码1，2，3，……，10的10个乒乓球放在一个箱子中，摇匀后，从中任意取一个，号码为小于7的奇数的概率是（ ）
5.有一张直角三角形纸片，两直角边AC=5cm，BC=10cm，将△ABC折叠，点B与点A重合，折痕为DE，则CD的长为（ ）
A B C D
二. 填空题（本题满分18分，共有6道小题，每小题3分）
8. “十一”黄金周期间，某风景区在7天假期中对每天上山旅游的人数统计如下表：
日期
10月1日
10月2日
10月3日
10月4日
10月5日
10月6日
10月7日
人数（万人）
1.2
1.2
2.3
1.8
1.8
1.2
0.8
这7天中上山旅游人数的众数是________万人，中位数是________万人。
9. 某商店购进一批商品，每件商品进价为a元，若要获利20%，则每件商品的零售价应定为________元。
11. 如图，如果
所在位置的坐标为（-1，-2），
所在位置的坐标为（2，-2），那么，
所在位置的坐标为________
三. 作图题（本题满分6分）
用圆规、直尺作图，不写作法，但要保留作图痕迹。
13. 某新建小区要在一块等边三角形的公共区域内修建一个圆形花坛。
（1）若要使花坛面积最大，请你在这块公共区域（如图）内确定圆形花坛的圆心P；
（2）若这个等边三角形的边长为18米，请计算出花坛的面积。
四. 解答题（本题满分78分，共有9道小题）
14. （本小题满分6分）
15. （本小题满分6分）
利群商厦对销量较大的A、B、C三种品牌的纯牛奶进行了问卷调查，共发放问卷300份（问卷由单选和多选题组成），对收回的265份问卷进行了整理，部分数据如下：
（1）最近一次购买各品牌纯牛奶用户比例如下图：
（2）用户对各品牌纯牛奶满意情况汇总如下表：
结合上述信息回答下列问题：
①A品牌牛奶的主要竞争优势是什么？请简要说明理由。
②广告对用户选择品牌有影响吗？请简要说明理由。
③你对厂家C有何建议？
16. （本小题满分6分）
小明和小刚想要利用如图的两个转盘玩游戏，请你帮助他们设计一个游戏，使游戏的规则对双方是公平的。
17. （本小题满分8分）
小明的家在某公寓楼AD内，他家的前面新建了一座大厦BC，小明想知道大厦的高度，但由于施工原因，无法测出公寓底部A与大厦底部C的直线距离，于是小明在他家的楼底A处测得大厦顶部B的仰角为
，爬上楼顶D处测得大厦的顶部B的仰角为
，已知公寓楼AD的高为60米，请你帮助小明计算出大厦的高度BC。
18. （本小题满分8分）
为响应承办“绿色奥运”的号召，某中学初三、2班计划组织部分同学义务植树180棵，由于同学们参与的积极性很高，实际参加植树活动的人数比原计划增加了50%，结果每人比原计划少栽了2棵树，问实际有多少人参加了这次植树活动？
19. （本小题满分10分）
如图，在等腰梯形ABCD中，AD//BC，M、N分别为AD、BC的中点，E、F分别是BM、CM的中点。
（1）求证：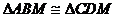
；
（2）四边形MENF是什么图形？请证明你的结论；
（3）若四边形MENF是正方形，则梯形的高与底边BC有何数量关系？并请说明理由。
20. （本小题满分10分）
某商厦试销一种成本为50元/件的商品，规定试销时的销售单价不低于成本，又不高于80元/件，试销中销售量y（件）与销售单价x（元/件）的关系可近似的看作一次函数（如图）。
（1）求y与x的关系式；
（2）设商厦获得的毛利润（毛利润＝销售额－成本）为s（元），则销售单价定为多少时，该商厦获利最大？最大利润是多少？此时的销售量是多少件？
21. （本小题满分12分）
如图，在矩形ABCD中，AB＝6米，BC＝8米，动点P以2米/秒的速度从点A出发，沿AC向点C移动，同时动点Q以1米/秒的速度从点C出发，沿CB向点B移动，设P、Q两点移动t秒（0<t<5）后，四边形ABQP的面积为S米2。
（1）求面积S与时间t的关系式；
（2）在P、Q两点移动的过程中，四边形ABQP与△CPQ的面积能否相等？若能，求出此时点P的位置；若不能，请说明理由。
22. （本小题满分12分）
操作：
在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点。图①，②，③是旋转三角板得到的图形中的3种情况。
研究：
（1）三角板绕点P旋转，观察线段PD和PE之间有什么数量关系？并结合图②加以证明。
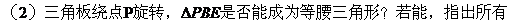
（3）若将三角板的直角顶点放在斜边AB上的M处，且AM：MB＝1：3，和前面一样操作，试问线段MD和ME之间有什么数量关系？并结合图④加以证明。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com