
2006年吉林省初中毕业生学业考试数学试卷(课改卷)
一、填空题(每小题2分,共20分)
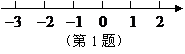 1.请你在数轴上用“
1.请你在数轴上用“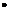 ”表示出比
”表示出比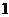 小
小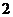 的数.
的数.
2.据报道,2006年全国高考报名总人数约为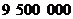 人,用科学记数法表示为_____人.
人,用科学记数法表示为_____人.
3.方程 的解是
的解是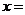 _______.
_______.
4.不等式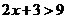 的解集是_______.
的解集是_______.
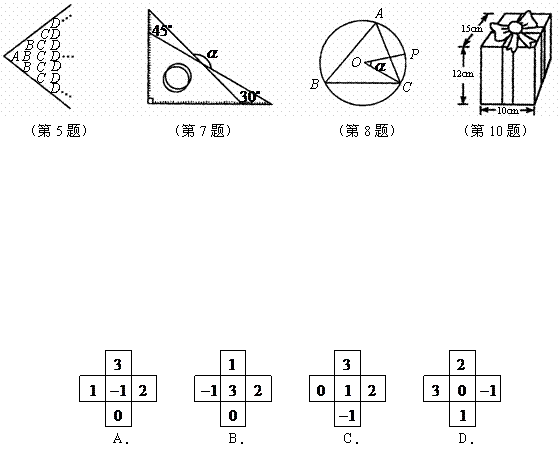
5.如图,按英语字母表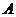 ,
,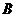 ,
,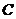 ,
, ,
,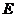 ,
,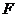 ,
,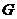 ,
,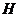 ,
,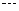 的顺序有规律排列而成的鱼状图案中,字母“
的顺序有规律排列而成的鱼状图案中,字母“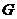 ”出现的个数为_______.
”出现的个数为_______.
6.若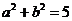 ,
,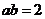 ,则
,则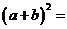 _______.
_______.
7.把一副三角板按如图方式放置,则两条斜边所形成的钝角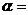 _______度.
_______度.
8.如图,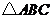 是
是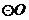 的内接三角形,
的内接三角形,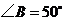 ,点
,点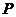 在
在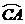 上移动(点
上移动(点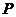 不与点
不与点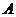 ,
,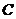 重合),则
重合),则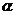 的变化范围是_______.
的变化范围是_______.
9.某工厂生产同一型号的电池.现随机抽取了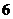 节电池,测试其连续使用时间(小时)分别为:
节电池,测试其连续使用时间(小时)分别为: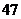 ,
,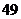 ,
, ,
,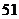 ,
, ,
,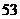 .这
.这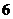 节电池连续使用时间的平均数为_______小时.
节电池连续使用时间的平均数为_______小时.
10.如图,把一个长方体的礼品盒用丝带打上包装,打蝴蝶结部分需丝带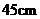 .那么打好整个包装所用丝带总长为_______
.那么打好整个包装所用丝带总长为_______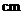 .
.
二、单项选择题(每小题3分,共18分)
11.把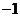 ,
,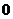 ,
,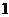 ,
,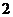 ,
,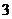 这五个数,填入下列方框中,使行、列三个数的和相等,其中错误的是( )
这五个数,填入下列方框中,使行、列三个数的和相等,其中错误的是( )
12.下列各点中,在反比例函数 图象上的是( )
图象上的是( )
A.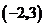 B.
B.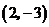 C.
C.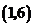 D.
D.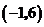
13.下列由数字组成的图形中,是轴对称图形的是( )
 |
14.小明家上个月支出共计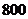 元,各项支出如图所示,其中用于教育上的支出是( )
元,各项支出如图所示,其中用于教育上的支出是( )
A.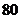 元 B.
元 B.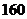 元 C.
元 C.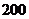 元 D.
元 D.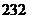 元
元
 |
 15.如图,把边长为
15.如图,把边长为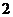 的正方形的局部进行图①~图④的变换,拼成图⑤,则图⑤的面积是( )
的正方形的局部进行图①~图④的变换,拼成图⑤,则图⑤的面积是( )
A.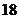 B.
B.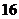 C.
C.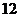 D.
D.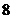
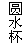
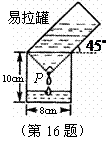 16.如图,在把易拉罐中的水倒入一个圆水杯的过程中,若水杯中的水在点
16.如图,在把易拉罐中的水倒入一个圆水杯的过程中,若水杯中的水在点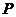 与易拉罐刚好接触,则此时水杯中的水深为( )
与易拉罐刚好接触,则此时水杯中的水深为( )
A.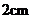 B.
B. C.
C.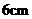 D.
D.
三、解答题(每小题5分,共20分)
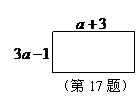 17.矩形的长和宽如图所示,当矩形周长为
17.矩形的长和宽如图所示,当矩形周长为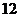 时,求
时,求 的值.
的值.
18.据某统计数据显示,在我国的 座城市中,按水资源情况可分为三类:暂不缺水城市、一般缺水城市和严重缺水城市.其中,暂不缺水城市数比严重缺水城市数的
座城市中,按水资源情况可分为三类:暂不缺水城市、一般缺水城市和严重缺水城市.其中,暂不缺水城市数比严重缺水城市数的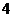 倍少
倍少 座,一般缺水城市数是严重缺水城市数的
座,一般缺水城市数是严重缺水城市数的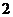 倍.求严重缺水城市有多少座?
倍.求严重缺水城市有多少座?
 |
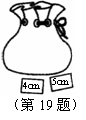 19.如图,口袋中有
19.如图,口袋中有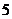 张完全相同的卡片,分别写有
张完全相同的卡片,分别写有 ,
,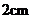 ,
, ,
, 和
和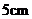 ,口袋外有
,口袋外有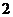 张卡片,分别写有
张卡片,分别写有 和
和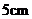 .现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,回答下列问题:
.现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,回答下列问题:
(1)求这三条线段能构成三角形的概率;
(2)求这三条线段能构成直角三角形的概率;
(3)求这三条线段能构成等腰三角形的概率.
20.如图,在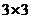 的方格内,填写了一些代数式和数.
的方格内,填写了一些代数式和数.
(1)在图1中各行、各列及对角线上三个数之和都相等,请你求出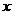 ,
,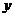 的值;
的值;
(2)把满足(1)的其它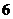 个数填入图2中的方格内.
个数填入图2中的方格内.
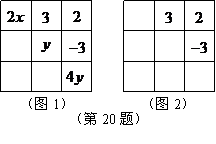 |
四、解答题(每小题6分,共18分)
21.某校七年级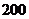 名女生的身高统计数据如下:
名女生的身高统计数据如下:
组别
身高/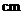
女生人数
第1组
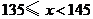

第2组
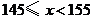
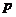
第3组
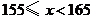
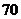
第4组
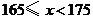
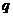
请你结合图表,回答下列问题:
(1)表中的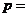 ___________,
___________,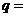 ___________;
___________;
(2)请把直方图补充完整;
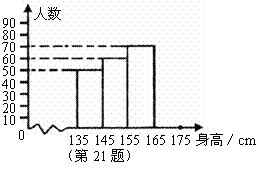 (3)这组数据的中位数落在第___________组.
(3)这组数据的中位数落在第___________组.
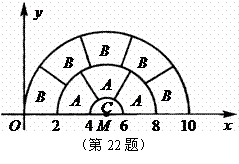 22.如图,圆心为点
22.如图,圆心为点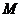 的三个半圆的直径都在
的三个半圆的直径都在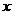 轴上,所有标注
轴上,所有标注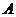 的图形面积都是
的图形面积都是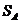 ,所有标注
,所有标注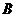 的图形面积都是
的图形面积都是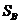 .
.
(1)求标注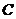 的图形面积
的图形面积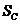 ;
;
(2)求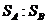 .
.
23.小明受《乌鸦喝水》故事的启发,利用量桶和体积相同的小球进行了如下操作:
 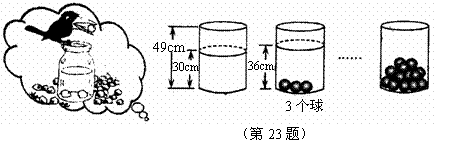 |
请根据图中给出的信息,解答下列问题:
(1)放入一个小球量桶中水面升高___________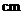 ;
;
(2)求放入小球后量桶中水面的高度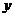 (
(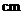 )与小球个数
)与小球个数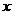 (个)之间的一次函数关系式(不要求写出自变量的取值范围);
(个)之间的一次函数关系式(不要求写出自变量的取值范围);
(3)量桶中至少放入几个小球时有水溢出?
五、解答题(每小题8分,共24分)
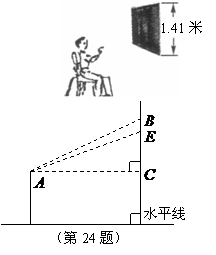
24.如图,小刚面对黑板坐在椅子上.若把黑板看作矩形,其上的一个字看作点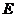 ,过点
,过点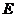 的该矩形的高为
的该矩形的高为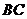 ,把小刚眼睛看作点
,把小刚眼睛看作点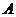 .现测得:
.现测得: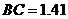 米,视线
米,视线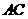 恰与水平线平行,视线
恰与水平线平行,视线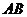 与
与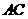 的夹角为
的夹角为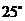 ,视线
,视线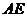 与
与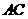 的夹角为
的夹角为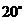 .
.
求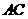 和
和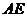 的长(精确到
的长(精确到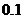 米)
米)
(参考数据: ,
,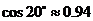 ,
,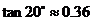 ,
,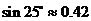 ,
,
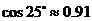 ,
,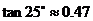 .)
.)
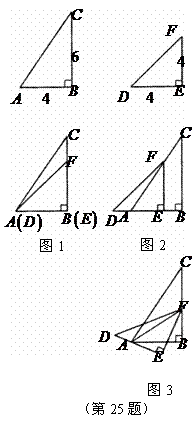
25.如图,在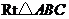 和
和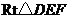 中,
中,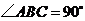 ,
,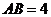 ,
,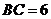 ,
,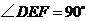 ,
,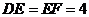 .
.
(1)移动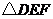 ,使边
,使边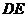 与
与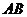 重合(如图1),再将
重合(如图1),再将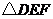 沿
沿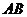 所在直线向左平移,使点
所在直线向左平移,使点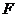 落在
落在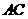 上(如图2),求
上(如图2),求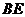 的长;
的长;
(2)将图2中的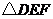 绕点
绕点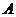 顺时针旋转,使点
顺时针旋转,使点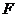 落在
落在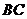 上,连结
上,连结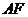 (如图3).请找出图中的全等三角形,并说明它们全等的理由.
(如图3).请找出图中的全等三角形,并说明它们全等的理由.
(不再添加辅助线,不再标注其它字母).
 |
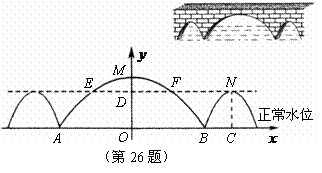 26.如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度
26.如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度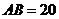 米,顶点
米,顶点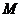 距水面
距水面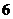 米(即
米(即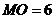 米),小孔顶点
米),小孔顶点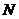 距水面
距水面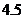 米(即
米(即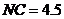 米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度
米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度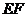 .
.
六、解答题(每小题10分,共20分)
27.如图,在平面直角坐标系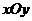 中,把矩形
中,把矩形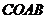 绕点
绕点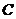 顺时针旋转
顺时针旋转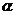 角,得到矩形
角,得到矩形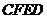 .设
.设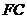 与
与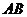 交于点
交于点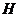 ,且
,且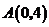 ,
,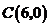 (如图1).
(如图1).
(1)当 时,
时,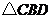 的形状是_____________;
的形状是_____________;
(2)当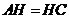 时,求直线
时,求直线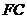 的解析式;
的解析式;
 (3)当
(3)当 时,(如图2).请探究:经过点
时,(如图2).请探究:经过点 ,且以点
,且以点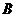 为顶点的抛物线,是否经过矩形
为顶点的抛物线,是否经过矩形 的对称中心
的对称中心 ,并说明理由.
,并说明理由.
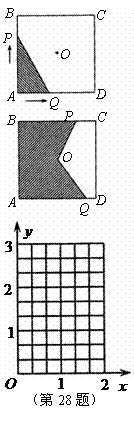 28.如图,正方形
28.如图,正方形 的边长为
的边长为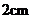 ,在对称中心
,在对称中心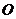 处有一钉子.动点
处有一钉子.动点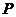 ,
, 同时从点
同时从点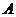 出发,点
出发,点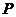 沿
沿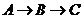 方向以每秒
方向以每秒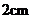 的速度运动,到点
的速度运动,到点
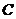 停止,点
停止,点 沿
沿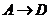 方向以每秒
方向以每秒 的速度运动,到点
的速度运动,到点 停止.
停止.
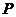 ,
, 两点用一条可伸缩的细橡皮筋联结,设
两点用一条可伸缩的细橡皮筋联结,设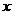 秒后橡皮筋扫过的
秒后橡皮筋扫过的
面积为 .
.
(1)当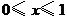 时,求
时,求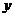 与
与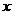 之间的函数关系式;
之间的函数关系式;
(2)当橡皮筋刚好触及钉子时,求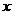 值;
值;
(3)当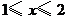 时,求
时,求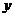 与
与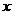 之间的函数关系式,并写出橡皮筋从
之间的函数关系式,并写出橡皮筋从
触及钉子到运动停止时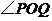 的变化范围;
的变化范围;
(4)当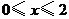 时,请在给出的直角坐标系中画出
时,请在给出的直角坐标系中画出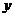 与
与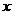 之间的
之间的
函数图象.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com