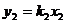(A)4?3 (B)3?2 (C)2?1
A (D)不确定,与P点的位置有
B
C
试题详情
三.解答题:(67分)
P 22.(5分)计算: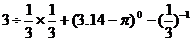 试题详情
23.(5分)解方程: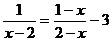 试题详情
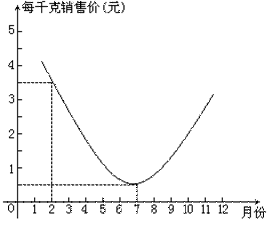 24. (6分)某农场种植一种蔬菜,销售员张平根据往年的销售情况,对今年这种蔬菜的销售价格进行了预测,预测情况如图,图中的抛物线(部分)表示这种蔬菜销售价与月份之间的关系.观察图象,你能得到关于这种蔬菜销售情况的哪些信息(至少写出两条)?求出函数的解析式。 24. (6分)某农场种植一种蔬菜,销售员张平根据往年的销售情况,对今年这种蔬菜的销售价格进行了预测,预测情况如图,图中的抛物线(部分)表示这种蔬菜销售价与月份之间的关系.观察图象,你能得到关于这种蔬菜销售情况的哪些信息(至少写出两条)?求出函数的解析式。
试题详情
25.(6分)如图所示,AB=AE,∠ABC=∠AED,BC=ED,点F是CD的中点. (1)求证:AF⊥CD; (2)在连结BE后,你还能得出什么新结论?请写出三个(不要求证明). 试题详情
试题详情
26.(7分)1900年,奥地利科学家兰德斯坦纳将人的血液分为A型、B型、AB型和O型四种类型,这就是ABO血型。此后,输血,就成为临床上实际可行的重要治疗措施。输血时,应以输入同型血为原则,也就是每种血型的人可以给自己同血型人输血。但在没有同型血而又情况紧急时,A型和B型的人可以给AB型的人输血,O型的人可以给各种血型的人输血。 (1)根据题意,利用ABO血型之间在输血时的相互关系填写下表(要求:用“+”或“-”填入相应的空格内): 献血者红细胞(含凝集原) 受血者 血清(含凝集原) A型(抗B) B型(抗A) AB型(无) O型(抗A、抗B) A型(A) - + - + B型(B) + - + A、B型(A、B) + - + O型(无) - - - - 注:“+”表示有凝集反应,“-”表示无凝集反应。 (2)一个O型血的人需要紧急输血,现有18人请求献血。其中,与A型血发生凝集者为9人,与B型血发生凝集者为7人,与A、B型血都发生凝集者和不发生凝集者共有8人。求这18人中可以实施献血的是几个人? 试题详情
试题详情
 已知: ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD, A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图). 已知: ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD, A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图).
试题详情
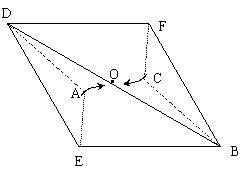 ⑴求证:四边形ABCD是矩形; ⑴求证:四边形ABCD是矩形;
试题详情
⑵在四边形ABCD中,求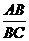 的值. 的值. 试题详情
28.(10分)快乐公司决定按左图给出的比例,从甲、乙、丙三个工厂共购买200件同种产品A,已知这三个工厂生产的产品A的优品率如右表所示. 甲 乙 丙 优品率 80% 85% 90% 试题详情
试题详情
 ⑵求快乐公司所购买的200件产品A的优品率; ⑵求快乐公司所购买的200件产品A的优品率;
⑶你认为快乐公司能否通过调整从三个工厂所购买的产品A的比例,使所购买的200件产品A的优品率上升3%.若能,请问应从甲厂购买多少件产品A;若不能,请说明理由. 试题详情
29.(10分) 如图,在矩形ABCD中,AD=8,点E是AB边上的一点,AE=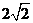 ,过D,E两点作直线PQ,与BC边所在的直线MN相交于点F。(1)求tan∠ADE的值; ,过D,E两点作直线PQ,与BC边所在的直线MN相交于点F。(1)求tan∠ADE的值; (2)点G是线段AD上的一个动点(不运动至点A,D),GH⊥DE垂足为H,设DG为x,四边形AEHG的面积为y,请求出y与x之间的函数关系式; 试题详情
(3)如果AE=2EB,点O是直线MN上的一个动点,以O为圆心作圆,使⊙O与直线PQ相切,同时又与矩形ABCD的某一边相切。问满足条件的⊙O有几个?并求出其中一个圆的半径 试题详情
 30.(10分)课题研究:现有边长为120厘米的正方形铁皮,准备将它设计并制成一个开口的水槽,使水槽能通过的水的流量最大. 30.(10分)课题研究:现有边长为120厘米的正方形铁皮,准备将它设计并制成一个开口的水槽,使水槽能通过的水的流量最大.
初三(1)班数学兴趣小组经讨论得出结论:在水流速度一定的情况下,水槽的横截面面积越大,则通过水槽的水的流量越大.为此,他们对水槽的横截面进行了如下探索: ⑴方案①:把它折成横截面为直角三角形的水槽(如图1). 若∠ACB=90°,设AC=x厘米,该水槽的横截面面积为y厘米2,请你写出y关于x的函数关系式(不必写出x的取值范围),并求出当x取何值时,y的值最大,最大值又是多少? 试题详情

方案②:把它折成横截面为等腰梯形的水槽(如图2). 试题详情
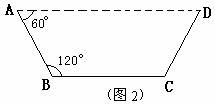 若∠ABC=120°,请你求出该水槽的横截面面积的最大值,并与方案①中的y的最大值比较大小. 若∠ABC=120°,请你求出该水槽的横截面面积的最大值,并与方案①中的y的最大值比较大小.
⑵假如你是该兴趣小组中的成员,请你再提供两种方案,使你所设计的水槽的横截面面积更大.画出你设计的草图,标上必要的数据(不要求写出解答过程). 试题详情
| 
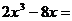 。
。 4.函数
4.函数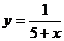 中,自变量
中,自变量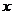 的取值范围是
。
的取值范围是
。 ,对称轴是__________________。
,对称轴是__________________。 有一位同学根据上表得出如下结论:①甲、乙两班学生的平均水平相同;②乙班优秀的人数比甲班优秀的人数多(每分钟输入汉字达150个以上为优秀);③甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大。上述结果正确的是__________________(填序号)。
有一位同学根据上表得出如下结论:①甲、乙两班学生的平均水平相同;②乙班优秀的人数比甲班优秀的人数多(每分钟输入汉字达150个以上为优秀);③甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大。上述结果正确的是__________________(填序号)。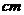 ,CD=8
,CD=8 ,那么AE的长为
,那么AE的长为
 ;
;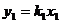 的图象通过P(2,3)点,且与函数
的图象通过P(2,3)点,且与函数