
2007届北师大课改实验区中考模拟试题(六)
 一.填空题(每题3分,共30分)
一.填空题(每题3分,共30分)
1.某公司员,月工资由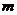 元增长了10%后达到____ _____元;
元增长了10%后达到____ _____元;
2.分解因式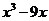 =_________
;
=_________
;
3.在函数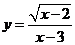 中,自变量
中,自变量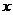 的取值范围是______
___;
的取值范围是______
___;
4.如图,在⊙O中,若半径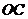 与弦
与弦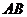 互相平分,且
互相平分,且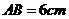 ,则
,则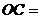 __ ___
__ ___ ;
;
5.要做两个形状为三角形的框架,其中一个三角形框架的三边长分别为4,5,6,另一个三角形框架的一边长为2,欲使这两个三角形相似,三角形框架的两边长可以是_________;
 6.三角形纸片
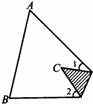
6.三角形纸片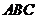 中,
中,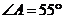 ,
,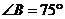 ,将纸片的一角折叠,
,将纸片的一角折叠,
使点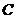 落在
落在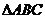 内(如图),则
内(如图),则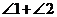 的度数为_______________;
的度数为_______________;
7.下面的扑克牌中,牌面是中心对称图形的是_______________;(填序号)

8.对于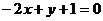 ,当
,当 时,
时,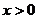 ;
;
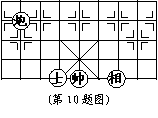 9.有两个完全相同的抽屉和3个完全相同的白色球,要求抽屉不能空着,那么第一个抽屉中有2个球的概率是_____;
9.有两个完全相同的抽屉和3个完全相同的白色球,要求抽屉不能空着,那么第一个抽屉中有2个球的概率是_____;
 10.如图,如果 所在位置的坐标为(
10.如图,如果 所在位置的坐标为(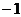 ,
,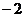 ), 所
), 所
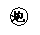 在位置的坐标为(
在位置的坐标为(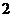 ,
,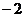 ), 那么, 所在位置的坐
), 那么, 所在位置的坐
标为 ;
二.选择题(以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请把正确选项的字母选入该题括号内.每小题4分,共24分)
11. 1纳米=
A、 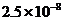 米 B、
米 B、 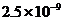 米 C、
米 C、 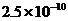 米 D、
米 D、 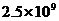 米
米
12.点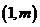 ,
,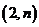 在函数
在函数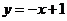 的图象上,则
的图象上,则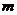 、
、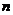 的关系是
( )
的关系是
( )
A、 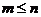 B、
B、 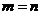 C、
C、
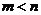 D、
D、 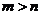
13.一个形式如圆锥的冰淇淋纸筒,其底面直径为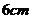 ,母线长为
,母线长为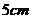 ,围成这样的冰淇淋纸筒所需纸片的面积是
( )
,围成这样的冰淇淋纸筒所需纸片的面积是
( )
A、 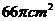 B、
B、 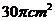 C、
C、 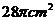 D、
D、 
14.如图,四边形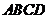 内接于⊙O,
内接于⊙O,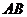 为⊙O的直径,
为⊙O的直径,
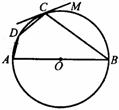
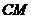 切⊙O于点
切⊙O于点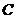 ,
,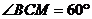 ,则
,则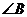 的正切值是
( )
的正切值是
( )
A、 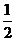 B、
B、 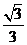
C、 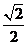 D、
D、 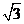
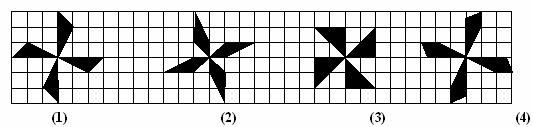
15.如图,在方格纸中有四个图形(1)、(2)、(3)、(4),其中面积相等的图形是 ( )A. (1)和(2) B. (2)和(3) C. (2)和(4) D. (1)和(4)


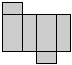
 16下面的4幅图中,经过折叠不能围成一个立体图的一幅是
( )
16下面的4幅图中,经过折叠不能围成一个立体图的一幅是
( )
A、 B、 C、 D、
三.解答题:
17.(本题满分8分)
先化简,再求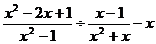 的值:,其中
的值:,其中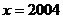 ,但是,甲抄错
,但是,甲抄错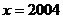 ,抄成
,抄成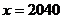 ,但他的计算结果仍然是正确的,你说是怎么回事?
,但他的计算结果仍然是正确的,你说是怎么回事?
18.(本题满分10分)
在本学期某次考试中,某校初二⑴、初二⑵两班学生数学成绩统计如下表:
分数
50
60
70
80
90
100
人数
二⑴班
3
5
16
3
11
12
二⑵班
2
5
11
12
13
7
请根据表格提供的信息回答下列问题:
⑴ 二⑴班平均成绩为_________分,二⑵班平均成绩为________分,从平均成绩看两个班成绩谁优谁次?
⑵ 二⑴班众数为________分,二⑵班众数为________分。从众数看两个班的成绩谁优谁次?____________________。
⑶已知二⑴班的方差大于二⑵班的方差,那么说明什么?
19.(本题满分9分)
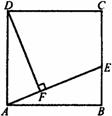
如图,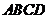 是正方形,点
是正方形,点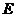 在
在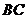 上,
上,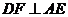 于
于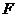 ,请你在
,请你在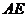 上确定一点
上确定一点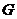 ,使
,使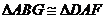 ,并说明理由。
,并说明理由。
 |
。
20.(本题满分12分)
集市上有一个人在设摊“摸彩”,只见他手拿一个黑色的袋子,内装大小、形状、质量完全相同的白球20只,且每一个球上都写有号码(1-20号)和1只红球,规定:每次只摸一只球。摸前交1元钱且在1――20内写一个号码,摸到红球奖5元,摸到号码数与你写的号码相同奖10元。
(1) 你认为该游戏对“摸彩”者有利吗?说明你的理由。
(2) 若一个“摸彩”者多次摸奖后,他平均每次将获利或损失多少元?
21.(本题满分12分)
小明和小亮进行百米赛跑,小明比小亮跑得快,如果两人同时起跑,小明肯定赢,现在小明让小亮先跑若干米,两人的路程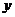 (米)分别与小明追赶时间
(米)分别与小明追赶时间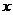 (秒)的函数关系如图所示。
(秒)的函数关系如图所示。
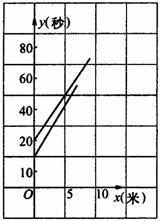 ⑴小明让小亮先跑了多少米?
⑴小明让小亮先跑了多少米?
⑵分别求出表示小明、小亮的路程与时间的函数关系式。
⑶谁将赢得这场比赛?请说明理由。
22.(本题满分9分)
掺望台AB高
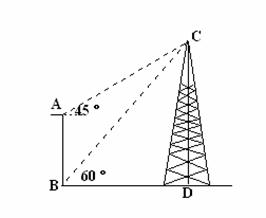
23.(本题满分12分)
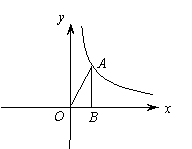
第一象限内的点A在一反比例函数的图象上,过A作AB⊥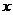 轴,垂足为B,连AO,已知△AOB的面积为4。
轴,垂足为B,连AO,已知△AOB的面积为4。
(1) 求反比例函数的解析式;
(2) 若点A的纵坐标为4,过点A的直线与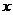 轴交于P,且△APB与△AOB相似,求所有符合条件的点P的坐标;
轴交于P,且△APB与△AOB相似,求所有符合条件的点P的坐标;
 (3)在(2)的条件下,过点P、O、A的抛物线是否可由抛物线
(3)在(2)的条件下,过点P、O、A的抛物线是否可由抛物线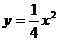 平移得到?若是,请说明由抛物线
平移得到?若是,请说明由抛物线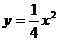 如何平移得到;若不是,请说明理由。
如何平移得到;若不是,请说明理由。
|