
2006年才上海市青浦区初三综合试卷
一、填空题(本题共12小题,每小题3分,满分36分)
1、计算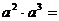 .
.
2、若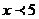 ,则
,则 =
.
=
.
3、因式分解: =
.
=
.
4、函数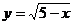 的定义域是
.
的定义域是
.
5、函数 的图象的两个分支分别在第二、四象限内,则
的图象的两个分支分别在第二、四象限内,则 的取值范围是
.
的取值范围是
.
6、当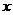 =
时,分式
=
时,分式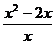 的值为零.
的值为零.
7、方程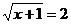 的解是
.
的解是
.
8、为了解决药品价格过高的问题,本市决定大幅度降低药品价格,其中将原价为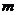 元的某种常用药降价20%,则降价后此药价格为
.
元的某种常用药降价20%,则降价后此药价格为
.
9、梯形的中位线长为4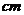 ,高为6
,高为6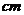 ,则该梯形的面积为
.
,则该梯形的面积为
.
10、已知两个相似三角形的周长比是1:3 ,则它们的面积比是 .
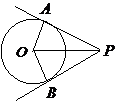 11、如图,
11、如图,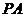 、
、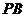 是⊙
是⊙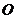 的两条切线,切点是
的两条切线,切点是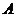 、
、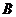 ,
,
如果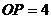 ,
,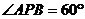 ,那么⊙
,那么⊙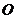 的半径是
.
的半径是
.
 12、如图,把一个直角三角形
12、如图,把一个直角三角形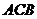 绕着
绕着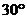 角的顶点
角的顶点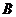
顺时针旋转,使点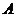 与
与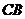 的延长线上的点E重合,
的延长线上的点E重合,
这时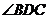 的度数是
.
的度数是
.
[本题每小题所列出的四个选项中,只有一个是正确的,把正确答案的代号填入括号内]
二、选择题(本大题共4题,每小题4分,满分16分)
13、下列说法正确的是……………………………………………………………… ( )
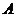 )
) 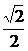 是分数
是分数
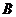 )实数
)实数 的倒数是
的倒数是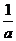
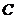 ) 负数没有平方根
) 负数没有平方根
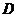 )绝对值等于本身的数是正数
)绝对值等于本身的数是正数
14、将二次函数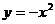 的图象向右平移3个单位,再向上平移2个单位,那么所得的二次
的图象向右平移3个单位,再向上平移2个单位,那么所得的二次
函数解析式为…………………………………………………………………… ( )
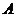 )
)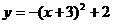
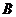 )
)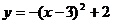
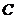 )
)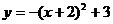
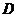 )
)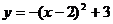
15、如图,已知四边形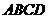 是平行四边形,下列结论中,不正确的是…… ( )
是平行四边形,下列结论中,不正确的是…… ( )

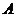 )当
)当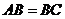 时,它是菱形
时,它是菱形
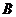 )当
)当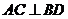 时,它是菱形
时,它是菱形
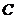 )当
)当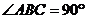 时,它是矩形
时,它是矩形
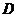 ) 当
) 当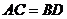 时,它是等腰梯形
时,它是等腰梯形
16、已知⊙ 和⊙
和⊙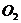 的半径分别为4
的半径分别为4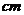 和
和 ,圆心距
,圆心距
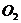 =5
=5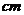 ,则⊙
,则⊙ 与⊙
与⊙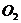
的公切线的条数为…………………………………………………………… ( )
 ) 1条
) 1条
 ) 2条
) 2条  ) 3条
) 3条
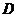 ) 4条
) 4条
三、(本大题共5题,第17、18题每题9分,第19~21题每题10分,满分48分)
17、已知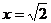 ,求
,求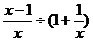 的值.
的值.
18、已知方程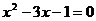 的两根为
的两根为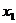 、
、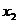 ,求
,求 的值.
的值.
19、解方程组:
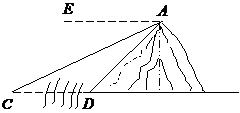 20、如图,河旁有一座小山,从山顶
20、如图,河旁有一座小山,从山顶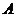 处测得河对岸点
处测得河对岸点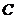 的俯角为
的俯角为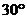 ,测得岸边点
,测得岸边点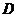 的俯角为
的俯角为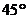 ,现从山顶
,现从山顶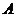 到河对岸点
到河对岸点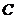 拉一条笔直的缆绳
拉一条笔直的缆绳 ,如果
,如果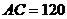 米,求河宽
米,求河宽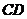 的长.
的长.
 21、如图,矩形
21、如图,矩形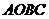 ,以
,以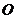 为坐标原点,
为坐标原点,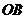 、
、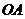 分别在
分别在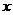 轴、
轴、 轴上,点
轴上,点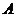 的坐标为(0,3),点
的坐标为(0,3),点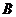 的坐标为(5,0),点
的坐标为(5,0),点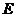 是
是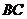 边上一点,如把矩形
边上一点,如把矩形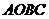 沿
沿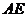 翻折后,
翻折后,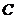 点恰好落在
点恰好落在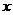 轴上点
轴上点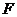 处.
处.
(1)求点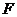 的坐标;
的坐标;
(2)求线段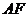 所在直线的解析式.
所在直线的解析式.
四、(本大题共4题,第22、23、24题每题12分,第25题14分,满分50分)
22、为了迎接初三数学学业考试,这学期共进行了10次数学专题测验,其中小丽的数学专题测验成绩情况如图所示:
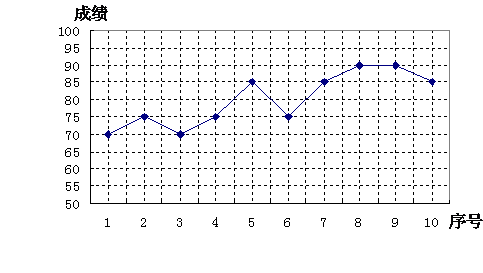
利用图中提供的信息,解答下列问题:
(1)小丽这10次数学专题测验成绩的平均数为 、中位数为 、方差为 ;
(2)如果将90分以上(含90分)成绩视为优秀,则小丽这10次数学专题测验成绩的优秀
率是 ;
(3)根据以上信息,请你对小丽同学提一条学习建议.
23、如图,已知⊙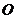 的弦
的弦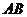 垂直于直径
垂直于直径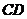 ,垂足为
,垂足为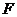 ,连接
,连接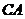 、
、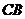 .
.
 (1)求证:
(1)求证: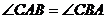 ;
;
(2)在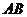 上有一点
上有一点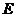 ,延长
,延长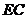 到点
到点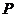 ,连接
,连接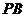 ,
,
若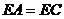 ,
,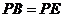 ,求证:
,求证: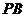 是⊙
是⊙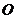 的切线.
的切线.
24、如图,已知二次函数 的图象经过点
的图象经过点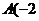 ,
,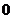 )、
)、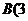 ,
,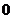 ),与
),与 轴交
轴交
 于点
于点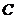 .
.
(1)求该二次函数的解析式;
(2)如在线段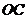 上有一点
上有一点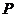 ,且点
,且点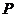 到点
到点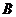 的
的
距离为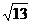 ,那么在
,那么在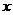 轴上是否存在点
轴上是否存在点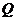 ,
,
使以点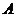 、
、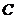 、
、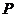 、
、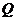 为顶点的四边形是梯
为顶点的四边形是梯
形?如存在,请求出点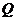 的坐标;如不存在,
的坐标;如不存在,
请说明理由.
25、如图,等边三角形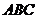 的边长为3,点
的边长为3,点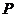 、
、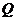 分别是
分别是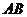 、
、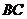 上的动点(点
上的动点(点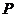 、
、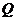
与三角形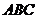 的顶点不重合),且
的顶点不重合),且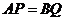 ,
, 、
、 相交于点
相交于点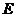 .
.
(1)如设线段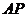 为
为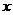 ,线段
,线段 为
为 ,求
,求 关于
关于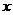 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(2)当△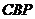 的面积是△
的面积是△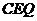 的面积的2倍时,求
的面积的2倍时,求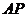 的长;
的长;
(3)点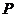 、
、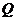 分别在
分别在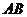 、
、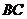 上移动过程中,
上移动过程中, 和
和 能否互相垂直?如能,请指
能否互相垂直?如能,请指
 出
出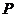 点的位置;如不能,请说明理由.
点的位置;如不能,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com