
2006-2007学年度北京市北师大附属实验中学第一学期期中试卷
一、选择题(本题共40分,每小题4分,在下列各题中的的四个选项中只有一个是正确的):
1.方程(m-1)x2+mx+l=0是关于x的一元二次方程,则m的值是( )
(A)任意实数 (B) m≠0 (C) m≠l (D) m≠-1
2.若x2-6x+k2是一个完全平方式,则k的值是( )
(A) 3 (B) -3 (C)±3 (D)以上都不对
3.下列一元二次方程中,两实根和为5的是( )
(A)x2-5x+8=0 (B) x2+5x-8=0
(C)x2+5x+8=0 (D) x2-5x-8=0
4.如图,在同一直角坐标系中表示y=ax2和y=ax+b(ab>O)的图象是( )
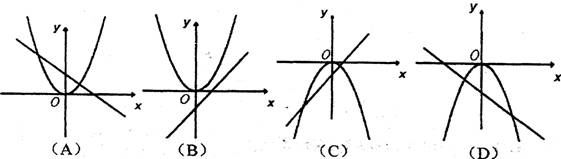
5.四张完全相同的卡片上,分别画有圆、矩形、等边三角形、等腰梯形,现在从中随机抽取一张,卡片上画的恰好是中心对称图形的概率为( )
(A)  (B)
(B)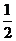 (C)
(C)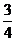 (D)
(D) 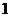
6.仔细读一读以下四个命题:(1)等弦对等弧;(2)等弧对等弦;(3)平分一条弧和它所对的弦的直线必过圆心;(4)平分弦的直径垂直于这条弦.其中正确的命题有( )
(A) 1个 (B) 2个 (C) 3个 (D)4个
7.0是△ABC的内心,∠A=800,则∠BOC的度数是( )
(A)1600 (B)1300 (C)1000 (D)400
8.一个圆锥形冰淇淋纸筒(无盖),其底面直径为
(A) 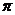 cm2 (B) 28
cm2 (B) 28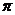 cm2 (C) 30
cm2 (C) 30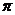 cm2 (D) 15
cm2 (D) 15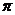 cm2
cm2
9.⊙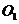 和⊙
和⊙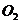 的半径分别为l和3,⊙
的半径分别为l和3,⊙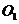 和⊙
和⊙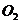 外切,则半径为4且与⊙
外切,则半径为4且与⊙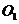 和⊙
和⊙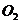 和都相切的圆有( )
和都相切的圆有( )
(A) 2个 (B) 3个 (C) 4个 (D) 5个
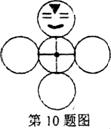
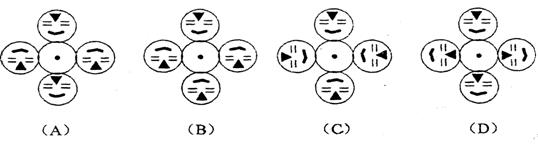
10.如上图,画有脸谱的圆与⊙0的半径相等,并绕⊙0按逆时针方向做无滑动的滚动(⊙0固定),则其中四个位置完全正确的是( )
二、填空题(本题共24分,每小题4分):
11.如果 是方程x2-cx+l=0的一个根,那么c的值是
.
是方程x2-cx+l=0的一个根,那么c的值是
.
12.己知抛物线y=3x2+4(a+1)x+3的顶点在x轴上,那么a的值是 .
13.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其它完全相同,小李通过多次摸球试验后发现其中摸到红色、黑色球的频率分别为O.1 5和0.45,则口袋中白色球的数目很可能是 .
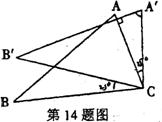
14.如图,将△ABC绕着点C按顺时针方向旋转250,B点落在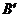 位置,A点落在
位置,A点落在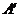 位置,若
位置,若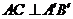 ,则∠BAC的度数是
.
,则∠BAC的度数是
.
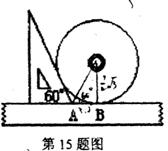
15.如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3.5cm,则此光盘的直径是 cm.
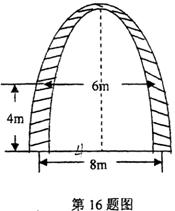
16.如图,某大学的校门是抛物线形水泥建筑物,大门的地面宽为8m,两侧距地面4m高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6m,则校门的高为 m(精确到0.1m,水泥建筑物厚度忽略不计).
三、解答题(本题共47分):
17. (本小题6分).解方程:2x2-2x-1=O
18. (本小题6分).已知关于x的方程kx2-4kx+k-5=0有两个相等的实数根,求k的值并解这个方程.
19. (本小题6分).在平面直角坐标系xOy中,直线y=-x绕点O顺时针旋转900得到直线l,直线l与二次函数y=x2+bx+2图象的一个交点为(m,3),试求二次函数的解析式.
20. (本小题6分).小明、小亮和小强三人准备下象棋,他们约定用 “抛硬币”的游戏方式来确定哪两个人先下棋,规则如下图:

(1)请你画出表示游戏一个回合所有可能出现的结果的树状图:
(2)求一个回合能确定两人先下棋的概率.
21. (本小题7分).机械加工需用油进行润滑以减小摩擦,某企业加工一台大型机械设备润滑用油量为90千克,用油的重复利用率为60%,按此计算,加工一台大型机械设备的实际耗油量为36千克.为了建设节约型社会,减少油耗,该企业的甲乙两个车间都组织了人员为减少实际油耗量进行攻关.
(1)甲车间通过技术革新后,加工一台大型机械设备润滑用油量下降到70千克,用油的重复利用率仍为60%,问甲车间技术革新后,加工一台大型机械设备的实际耗油量是多少千克?
(2)乙车间通过技术革新后,不仅降低了润滑用油量,同时也提高了重复利用率,并且发现在技术革新前的基础上,润滑用油量每减少1千克,用油的重复利用率将增加1.6%,这样乙车间加工一台大型机械设备的实际耗油量下降到12千克。问乙车间技术革新后,加工一台大型机械设备的润滑用油量是多少千克?用油的重复利用率是多少?
解方程: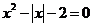
解:(1)当x≥O时,原方程化为x2-x-2=0,解得:x1=2,x2=-1(不合题意,舍去).
(2)当x<O时,原方程化为x2+x-2=0,解得:x1=1(不合题意,舍去),x2=-2
∴原方程的根是x1=2,x2=-2.
请参照例题解方程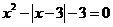 ,则此方程的根是
.
,则此方程的根是
.
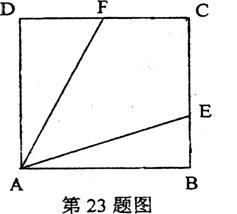
23.(本小题6分)如图.正方形ABCD中,E、F分别在边BC、CD上,∠EAF=450,BE=2,CF=3.
求:正方形的边长.
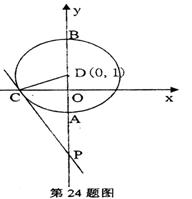
24.(本小题6分).己知:如图,⊙D交y轴于A、B,交x轴于C,过点C的直线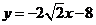 与y轴交于P,D点坐标(0,1)
与y轴交于P,D点坐标(0,1)
求证:PC是⊙D的切线.
四、解答题(本题9分):
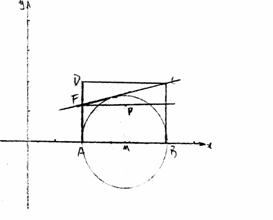
25.矩形ABCD的边长AB=3,AD=2,将此矩形放在平面直角坐标系中,使AB在x轴的正半轴上,点A在点B的左侧,另两个顶点都在第一象限,且直线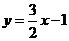 经过这两个顶点中的一个.
经过这两个顶点中的一个.
(1)求A、B、C、D四点坐标.
(2)以AB为直径作⊙M,记过A、B两点的抛物线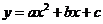 的顶点为P.
的顶点为P.
①若P点在⊙M和矩形内,求a的取值范围.
②过点C作CF切⊙M于E,交AD于F,当PF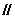 AB时,求抛物线的函数解析式.
AB时,求抛物线的函数解析式.
五、选做题(本题共6分,每小题3分):
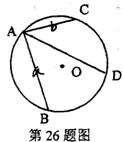
26.如图,在⊙O中,弦AB⊥AC,AB=a,AC=b,弦AD平分∠BAC.求AD的长(用a、b表示).
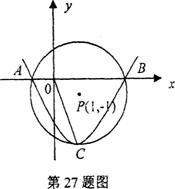
27.如图,在平面直角坐标系中,以点P(1,-1)为圆心,2为半径作圆,交x轴A、B两点,抛物线
y=ax2+bx+c(a>O)过点A、B,且顶点C在⊙P上.
(1)求抛物线的解析式;
(2)在抛物线上是否存在一点D,使线段OC与PD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com