
2006-2007学年度上学期期末教学质量调查
初四数学试题
(时间100分钟 总分120分)
一、选择题:(本题共12小题,第1~8小题,每小题3分,第9~12小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是正确的,请你把正确的选项选出来,把选项的代号填在下面表格中。)
1.在△ABC中,sinB=cos(90°-∠C)=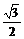 ,那么△ABC是
,那么△ABC是
(A)等腰三角形 (B)等边三角形 (C)直角三角形 (D)等腰直角三角形
2.在△ABC中,∠C=900 ,tanA=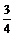 ,那么cosB等于
,那么cosB等于
 (A)
(A)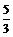 (B)
(B)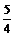 (C)
(C)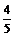 (D)
(D)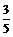
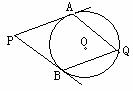
3.P是⊙O外一点,PA、PB切⊙O于点A、B,Q是优弧
AB上的一点,如图,设∠APB=60°,,则∠AQB=
(A)30°(B)40°(C)50°(D)60°
4.如图所示,边长分别为1和2的两个正方形,其一边在
同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为 ,大正方形内除去小正方形部分的面积为
,大正方形内除去小正方形部分的面积为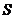 (阴影部分),那么
(阴影部分),那么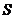 与
与 的大致图象应为
的大致图象应为
 |
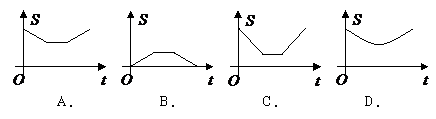
5.在Rt△ABC中,已知两直角边的长分别为5cm、12cm,则该直角三角形外接圆的半径与内切圆的半径分别为
 (A)6cm和2cm (B)7.5cm和4cm
(A)6cm和2cm (B)7.5cm和4cm
(C)6.5cm和2cm (D)6.5cm和3cm
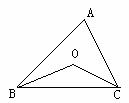
6.如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,
则∠BOC=
(A)130° (B)100° (C)50° (D)65°
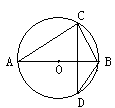 7.如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,
7.如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,
BC=6,AC=8,则sin∠ABD的值是
(A)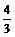 (B)
(B)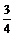 (C)
(C)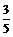 (D)
(D)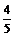
8.已知直线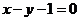 与抛物线
与抛物线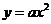 相切,则
相切,则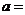
 (A)
(A)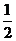 (B)
(B)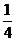 (C)
(C)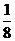 (D)
(D)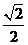
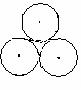
9.如图,某城市公园的雕塑是由三个半径为1m的圆两两相切
立在水平的地面上,则雕塑的最高点到地面的距离为
(A)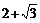 (B)
(B)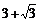 (C)
(C) (D)
(D)
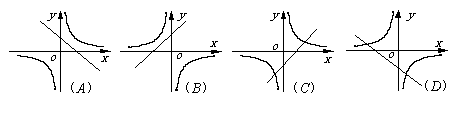 10.函数 y=
10.函数 y=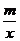 与y=mx-m(m≠0)在同一平面直角坐标系中的大致图象是
与y=mx-m(m≠0)在同一平面直角坐标系中的大致图象是
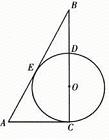
11.如图,在Rt△ABC中,AC=5,BC=12,⊙O分别与边AB、AC相切,切点分别为E、C,则⊙O的半径是
(A)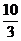 (B)
(B)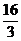 (C)
(C)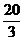 (D)
(D)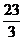
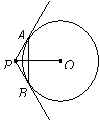 12.如图,直线
12.如图,直线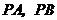 是⊙O的两条切线,
是⊙O的两条切线,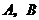 分别为切点,
分别为切点,
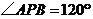 ,OP=8 cm,则弦
,OP=8 cm,则弦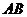 的长为
的长为
(A)4 cm (B)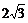 cm (C)
cm (C)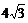 cm (D)
cm (D)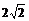 cm
cm
二、填空题:(本题共6小题,每小题4分,共24分)请把最终结果直接填在横线上。
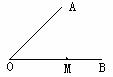 13.如图,已知∠AOB=45°,M为OB上一点,且OM=5cm,以M为圆心,以r=4cm为半径作圆,圆M与直线OA的位置关系是________.
13.如图,已知∠AOB=45°,M为OB上一点,且OM=5cm,以M为圆心,以r=4cm为半径作圆,圆M与直线OA的位置关系是________.
14.抛物线y=(k+1)x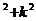 -9开口向下,且经过原点,则k=______.
-9开口向下,且经过原点,则k=______.
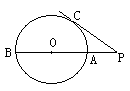 15.如图,已知AB是⊙O的直径,P为BA延长线上一点,PC切⊙O于C,若⊙O的半径是4cm,∠P=30°,则PC=_____cm, 弧AC的长是______cm.
15.如图,已知AB是⊙O的直径,P为BA延长线上一点,PC切⊙O于C,若⊙O的半径是4cm,∠P=30°,则PC=_____cm, 弧AC的长是______cm.
16.某市在旧城改造中计划在一块如图所示的三角形空 地上种植某种草皮以美化环境,AB=20m,AC=30m.已知这种草皮每平方米a元,则购买这种草皮至少需要___________元.
 17.在平面直角坐标系内,将抛物线y=2x2向左平移1个
17.在平面直角坐标系内,将抛物线y=2x2向左平移1个
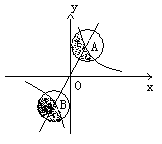 单位,再向下平移7个单位,所得到的抛物线的解析式是
单位,再向下平移7个单位,所得到的抛物线的解析式是
___________________.
18.如图,正比例函数和反比例函数的图象相交于A、B 两点,分别以A、B两点为圆心,画与y轴相切的两个圆。若点A的坐标为(1,2),则图中两个阴影面积的和是__________.
三、解答题:(本题共6 小题,共56分.解答题要用数学符号或文字写出解答过程或演算步骤)
19.(本题满分6分)
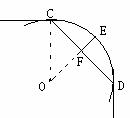 如图,一条公路的转弯处是一段圆弧
如图,一条公路的转弯处是一段圆弧 , 点O是
, 点O是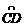 所在圆的圆心,其中CD=600m,
E为
所在圆的圆心,其中CD=600m,
E为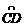 上一点,且OE⊥CD,垂足为F,EF=90m,求这段弯路的半径。
上一点,且OE⊥CD,垂足为F,EF=90m,求这段弯路的半径。
20.(本题满分8分)
元旦联欢会前某班布置教室,同学们利用彩纸条粘成一环套一环的彩纸链,小颖测量了部分彩纸链的长度,她得到的数据如下表:
纸环数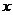 (个)
(个)
1
2
3
4
……
彩纸链长度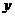 (cm)
(cm)
19
36
53
70
……
(1)把上表中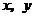 的各组对应值作为点的坐标,在如图的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在如图的平面直角坐标系中描出相应的点,猜想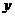 与
与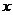 的函数关系,并求出函数关系式;
的函数关系,并求出函数关系式;
(2)教室天花板对角线长
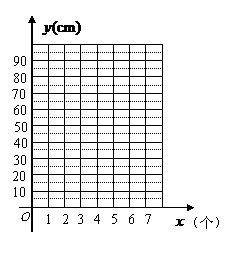
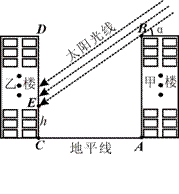
21. (本题满分10分)
如图,已知某小区的两幢10层住宅楼间的距离为AC=30 m,由地面向上依次为第1层、第2层、…、第10层,每层高度为
(1) 用含α的式子表示h(不必指出α的取值范围);
(2) 当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光 ?
22. (本题满分10分)
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系。
(1)求出以这一部分抛物线为图象的函数解析式,并写出x的取值范围;
 (2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?
(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?
23.(本题满分10分)
如图6,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度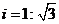 ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为 ,在山坡的坡顶D处测得铁架顶端
,在山坡的坡顶D处测得铁架顶端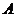 的仰角为
的仰角为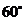 .
.
(1)求小山的高度;(4分)
(2)求铁架的高度.( ,精确到
,精确到
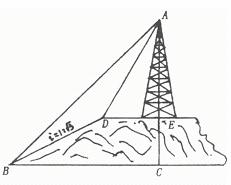
24.(本题满分12分)
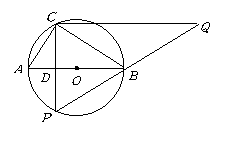
直径为5的⊙O中,直径AB的不同侧有定点C和动点P,已知BC:CA=4:3,点P在 上运动,过点
上运动,过点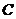 作
作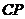 的垂线,与
的垂线,与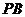 的延长线交于点Q.(1)当点
的延长线交于点Q.(1)当点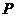 运动到与点C关于直径
运动到与点C关于直径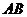 对称时,求CQ的长;
对称时,求CQ的长;
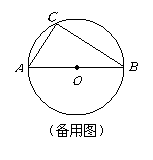 (2)当点
(2)当点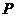 运动到什么位置时,CQ取到最大值,并求出此时CQ的长.
运动到什么位置时,CQ取到最大值,并求出此时CQ的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com