
2007年初中学业水平测试数学试卷
第Ⅰ卷
注意事项:
1.本试题分第Ⅰ卷和第Ⅱ卷两部分,共8页.第Ⅰ卷(1~2页)为选择题,共30分;第Ⅰ卷(3~8页)为非选择题,共70分.试题满分100分,考试时间90分钟.
2.答题前,请将密封线内的各项目填写清楚.选择题选出答案后,一律将其字母标号填写在第Ⅰ卷上的第Ⅰ卷答案栏内,不能答在第Ⅰ卷上.
第Ⅰ卷(选择题共30分)
一、选择题:本大题共10小题,每小题3分,共30分.在每小题所给的四个选项中,只有一项是符合题目要求的.
1.?-4?等于
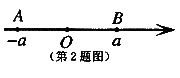 (A) -4 (B)4 (C)
(A) -4 (B)4 (C) 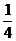 (D)?
(D)?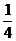
2.如图,数轴上A、B两点所表示的两个数的
(A)和为正数 (B)和为负数
(C)积为正数 (D)积为负数
3.若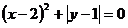 ,则x-y的值为
,则x-y的值为
(A)-1 (B)5 (C)1 (D)-5
4.下列运算中正确的是( )
(A)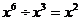 (B)
(B)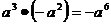
(C)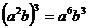 (D)
(D)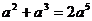
5.在同一直角坐标系中,函数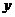 =
=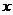 +l与
+l与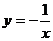 的图像大致为
的图像大致为
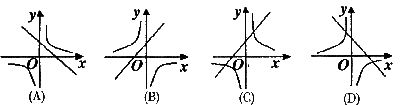
6.在一次男子马拉松长跑比赛中,抽得7名选手的成绩如下(单位:分):
136 145 129 180 124 154 145
这组样本数据的中位数和众数分别是
(A) 145 136 (B)145 145 (C)136 145 (D)154 136
7.下列说法正确的是
(A)过一点有且只有一条直线与已知直线平行
(B)同位角相等
(C)位似的两个图形一定相似
(D)三个点确定一个圆
8.已知两个圆的半径分别为3和4,圆心距为7,那么这两个圆的位置关系是
(A)内切 (B)外切 (C)外离 (D)相交
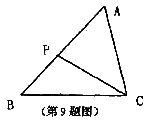 9.如图,在△ABC中,P是AB边上的一点,连接CP,以下条件中,不能判定△ACP∽△ABC的是
9.如图,在△ABC中,P是AB边上的一点,连接CP,以下条件中,不能判定△ACP∽△ABC的是
(A)∠ACP=∠B
(B) ∠APC=∠ACB
(C)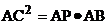
(D)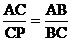
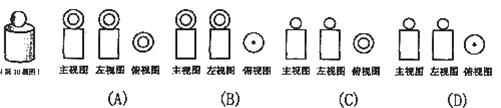
10.“圆柱与球的组合体”如图所示,则它的三视图是
第Ⅱ卷(非选择题共70分)
注意事项:
1.第Ⅰ卷共6页,用钢笔或圆珠笔直接答在试卷上.
2.答题前,请将密封线内的各项目填写清楚.
二、填空题:本大题共8小题,每小题4分,共32分.把答案填在题中横线上.
 11.
11.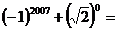 _____________
_____________
12.一元二次方程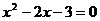 的根是___________
的根是___________
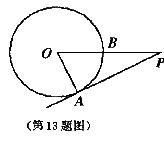
13.如图,PA为⊙O切线,A为切点,PO交⊙O于点B,PA=8,OA=4,则tan∠APO的值为_______.
14.在一个不透明的袋子中装有4个黑球和2个白球,这些球的形状、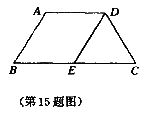 大小、质地等完全相同.若随机从袋子中摸出一球,则摸到黑球的概率是______________.
大小、质地等完全相同.若随机从袋子中摸出一球,则摸到黑球的概率是______________.
15.如图,在等腰梯形ABCD中,AD∥BC,∠B=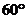 ,DE∥AB,则△DEC是_______三角形.(填:“不等边”、“等腰”或“等边”之一)
,DE∥AB,则△DEC是_______三角形.(填:“不等边”、“等腰”或“等边”之一)
16.如图,分别连接第1个等边三角形三边的中点得到第2个图形,再分别连接第2个图形中的中间小三角形三边的中点得到第3个图形,按此方法继续下去.已知第1个图形中三角形的面积为S,则第5个图形中中间最小的三角形的面积为______________.
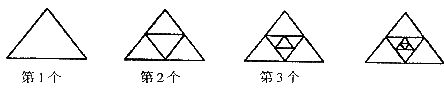
(第16题图)
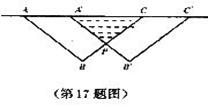 17.如图,把等腰Rt△ABC沿AC方向平移到等腰Rt△A′ B′C′的位置时,它们重叠部分的面积是Rt△ABC面积的
17.如图,把等腰Rt△ABC沿AC方向平移到等腰Rt△A′ B′C′的位置时,它们重叠部分的面积是Rt△ABC面积的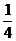 .若
.若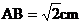 ,则它移动的距离AA′=___________ Cm.
,则它移动的距离AA′=___________ Cm.
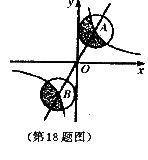 18.如图,正比例函数和反比例函数的图像相交于A、B两点,分别以A、B两点为圆心,画与
18.如图,正比例函数和反比例函数的图像相交于A、B两点,分别以A、B两点为圆心,画与 轴相切的两个圆.若点A的坐标为(1,2),则图中两个阴影部分的面积的和是__________.
轴相切的两个圆.若点A的坐标为(1,2),则图中两个阴影部分的面积的和是__________.
三、解答题:本大题共5小题,满分38分.解答应写出文字说明、证明过程或推演步骤.
19.(本小题满分5分)
有这样一道题:“计算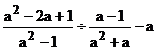 的值,其中a=2007”,甲同学把“a=2007”错抄成了“a=2070”,但他的计算结果也是正确的,你能说明这是为什么吗?
的值,其中a=2007”,甲同学把“a=2007”错抄成了“a=2070”,但他的计算结果也是正确的,你能说明这是为什么吗?
20.(本小题满分7分)
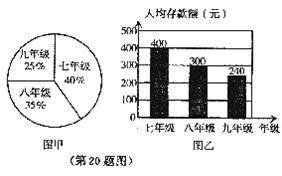 为了帮助贫困失学儿童,团市委发起“爱心储蓄”活动,鼓励学生将自己的压岁钱和零花钱存入银行,定期一年,到期后可取回本金,而把利息捐给贫困失学儿童.某中学共有学生1200人,图甲是该校各年级学生人数比例分布的扇形统计图,图乙是该校学生人均存款情况的条形统计图.
为了帮助贫困失学儿童,团市委发起“爱心储蓄”活动,鼓励学生将自己的压岁钱和零花钱存入银行,定期一年,到期后可取回本金,而把利息捐给贫困失学儿童.某中学共有学生1200人,图甲是该校各年级学生人数比例分布的扇形统计图,图乙是该校学生人均存款情况的条形统计图.
(1)九年级学生人均存款多少元;
(2)该校学生人均存款多少元;
(3)银行一年期定期存款的年利率是2.79%(“爱心储蓄”免收利息税),且每403元能提供给一位失学儿童一学年的基本费用,那么该校一学年能帮助多少贫困失学的儿童?
21.(本小题满分8分)
“五.一”黄金周期间,甲、乙两商店以同样价格出售同样的商品,但推出不同的优惠方案:在甲店累计购买100元商品后,再购买的部分按原价的90%收费;在乙店累计购买200元商品后,再购买的部分按原价的80%收费.若小明累计购物超过200元.
(1)请分别写出小明在甲、乙两商店实际付费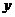 元与累计购物
元与累计购物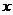 元之间的函数关系式;
元之间的函数关系式;
(2)选择在哪家商店购物,小明能获得更多的优惠?
 22.(本小题满分8分)
22.(本小题满分8分)
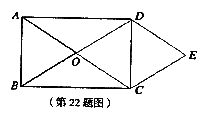
如图,矩形A8CD的对角线相交于点O,DE∥AC,CE∥BD。
(1)求证:四边形OCED是菱形;
(2)试写出使四边形OCED是正方形的一个条件.
23.(本小题满分10分)
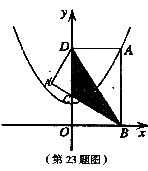 如图,在平面直角坐标系
如图,在平面直角坐标系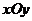 中,过A在抛物线
中,过A在抛物线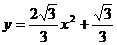 上,过A作AB⊥
上,过A作AB⊥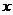 轴于点B,AD⊥
轴于点B,AD⊥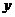 轴于点D,将矩形ABOD沿对角线BD折叠后得A的对应点为A′,A′B与OD交于点C,重叠部分(阴影)为△BDC.
轴于点D,将矩形ABOD沿对角线BD折叠后得A的对应点为A′,A′B与OD交于点C,重叠部分(阴影)为△BDC.
(1)求证:△BDC是等腰三角形;
(2)如果A点的坐标是(1, ),求△BDE的面积;
),求△BDE的面积;
(3)在(2)的条件下,求直线BC的解析式,并判断点A′是否落在已知的抛物线上?请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com