
2006-2007学年度菏泽市定陶县初三第二学期期中测评
数学试题
一、选择题(每小题3分,共36分)
1.如果 ,则a的取值是
( )
,则a的取值是
( )
A.a<0 B.a≤
2.估算 的值
( )
的值
( )
A.在5和6之间 B.在6和7之间 C.在7和8之间 D.在8和9之间
3.下面四个图形都是由相同的六个小正方形纸片组成,小正方形上分别贴有北京2008年奥运会五环标志和吉祥物五个福娃的卡通画,如果分别用“贝、晶、欢、迎、妮”五个字来表示五个福娃,那么折叠后能围成如图所示正方体的是 ( )
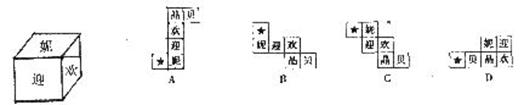
4.下列因式分解中,结果正确的是 ( )
A.
B.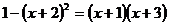
C.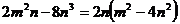
D.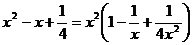
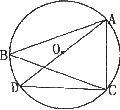
5.如图,△ABC内接于⊙O、AD是⊙O的直径,连接CD,若⊙O的半径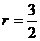 ,AC=2,则cosB的值为
(
)
,AC=2,则cosB的值为
(
)
A.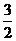 B.
B.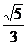 C.
C.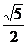 D.
D.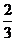
6.下列说法正确的是 ( )
A.一颗质地均匀的骰子已连续抛掷了200次,抛掷出5点的次数最少,则201次一定抛掷出5点
B.某种彩票中奖率是1%,因此买100张该种彩票一定会中奖
C.天气预报说,明天下雨的概率是50%,所以明天将有一半时间在下雨
D.抛掷一枚图钉、钉尖着地和朝上的概率不相等
7.为了美观,要用彩色纸对一个底面半径为
A.60° B.90° C.120° D.150°
8.如图在四边形ABCD中,AD//BC,E是AB的中点,若△DEC的面积为S,则四边形ABCD的面积为 ( )
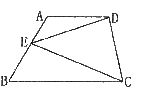
A.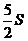 B.2S C.
B.2S C.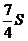 D.
D.
9.小兰和小芳分别用掷A、B两枚骰子的方法来确定P(x,y)的位置,她们规定:小兰掷得的点数为x,小芳掷得的点数为y,那么她们各掷一次所确定的点落在双曲线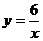 上的概率为
( )
上的概率为
( )
A.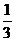 B.
B.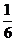 C.
C. D.
D.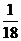
10.已知二次函数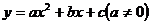 的图象如图所示。在下列结论 ( )
的图象如图所示。在下列结论 ( )
①c<0 ②a-b+c>0
③方程 有两个不相等的实数根
有两个不相等的实数根
④y随x的增大而增大中正确的个数是
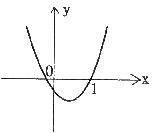
A.1个 B.2个 C.3个 D.4个
11.计算: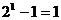
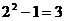
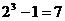

 ……归纳各计算结果中的个位数字规律猜测
……归纳各计算结果中的个位数字规律猜测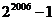 的个位数字是 ( )
的个位数字是 ( )
A.1 B.
12.某公司为赶制一批产品,先派甲车间单独工作2天,而后又派乙车间也参与生产,直至完成800件的产品任务,生产产品的件数与生产天数之间的函数关系如图所示,那么乙参与生产的天数是 ( )
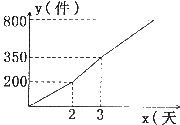
A.6天 B.5天 C.4天 D.3天
二、填空题(每题3分,共24分)
13.若2-m与
14.如图,将4根木条钉成的矩形木框变形成平行四边形ABCD的形状,并使面积为原矩形面积的一半,则这个平行四边形的一个最小内角的值等于 .

15.反比例函数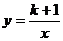 的图象上有两点A、B坐标分别是(x1,y1)(x2,y2),若x1<0<x2时,yl>y2,则k的取值范围是 .
的图象上有两点A、B坐标分别是(x1,y1)(x2,y2),若x1<0<x2时,yl>y2,则k的取值范围是 .
16.如图数轴上与1、 对应的点分别为A、B,点B关于点A的对称点为C,设点C表示的数为
对应的点分别为A、B,点B关于点A的对称点为C,设点C表示的数为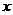 ,则
,则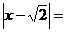 .
.
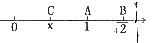
17.用“X”定义新运算时,对于任意实数a,b都有aXb=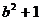 ;例如:7X4=
;例如:7X4=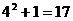 ,那么5X3= .当m为实数时,mX(mX2)= .
,那么5X3= .当m为实数时,mX(mX2)= .
18.如图,以BC为直径在半径为2,圆心角为90°的扇形内部作半圆交弦AB于点D,连接CD,则阴影部分的面积是 .

19.⊙O到直线 的距离为d,⊙O的半径为R,若d、R是方程
的距离为d,⊙O的半径为R,若d、R是方程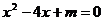 的两根,且直线
的两根,且直线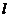 与⊙O相切,则m= .
与⊙O相切,则m= .
20.已知抛物线 经过点A(一2,7),B(6,7),C(3,一8)则该抛物线上纵坐标为一8的另一点的坐标是 .
经过点A(一2,7),B(6,7),C(3,一8)则该抛物线上纵坐标为一8的另一点的坐标是 .
三、解答题:(共60分)
23.(12分)求值:
(1)计算: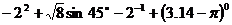
(2)求代数式的值。已知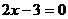 .
.
求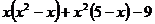 的值
的值
(3)课堂上李老师给大家出了这样一道题,当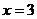 ,
,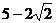 ,
,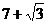 时,求代数式
时,求代数式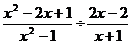 的值.小明一看“太复杂了怎么算呢?”你能帮小明解决这个问题吗?请你写出具体过程.
的值.小明一看“太复杂了怎么算呢?”你能帮小明解决这个问题吗?请你写出具体过程.
24.(8分)有两个可以自由转动的均匀转盘A、B分别被分成4等份、3等份,如图所示,小伟和小强同学用这个转盘做游戏,游戏规则如下:
①分别转动转盘A和B.
②两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止)
③如果和为0小伟获胜,否则小强获胜.
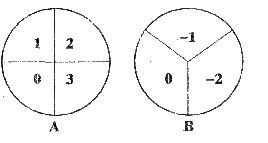
(1)用列表或树状图求小伟获胜的概率;
(2)你认为这个游戏对双方公平吗?请说明理由
25.(8分)如图矩形ABCD的对角线AC、BD相交于点O、E、F分别是OA、OB的中点.

(1)求证:△ADE≌△BCF
(2)若AD=
26.(10分)如图AB、AC分别是⊙O的直径和弦,点D为劣弧 上的一点,弦ED分别交⊙O于点E,交AB于点H,交AC于点F,过C点的切线交ED的延长线于点P.
上的一点,弦ED分别交⊙O于点E,交AB于点H,交AC于点F,过C点的切线交ED的延长线于点P.

(1)若PC=PF,求证:AB⊥ED
(2)点D在劣弧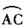 的什么位置时,才能使
的什么位置时,才能使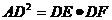 为什么?
为什么?
27.(10分)在2006年青岛崂山樱桃节前夕某果品批发公司为指导今年的樱桃销售,对往年的市场销售情况进了调查,统计得到如下数据:
销售价x(元/千克)
…
25
24
23
22
…
销售量y(千克)
…
2000
2500
3000
3500
…
(1)根据以上信息求出y与x之间的函数关系.
(2)若樱桃进价为13元/千克,试求销售利润P(元)与销售价x(元/千克)之间的函数关系,并求出当x为何值时,P的值最大?
28.(12分)已知m,n是方程 的两个实数根,且m<n.抛物线
的两个实数根,且m<n.抛物线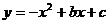 的图象经过点A(m,0),B(0,n).
的图象经过点A(m,0),B(0,n).
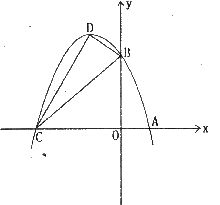
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与x轴的另一个交点为C,抛物线的顶点D.
试求出C、D的坐标和△BCD的面积.
(3)P是线段OC上的一点,过点P作PH⊥x轴与抛物线交于H点,若直线BC把APCH分成面积之比为2:3的两部分,请求出P点的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com