
2006--2007学年度菏泽市定陶县第二学期期中测评
初二数学试题
一、选择题(每小题3分,共33分)
1.有理式①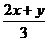 ; ②
; ②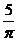 ; ③
; ③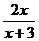 ; ④
; ④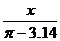 中是分式的是
中是分式的是
A.①② B.②③④ C.③ D.②④
2.要使分式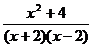 有意义,满足的条件是
有意义,满足的条件是
A.x≠O B.x≠
3.分式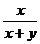 ,
,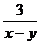 ,
,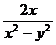 ,
,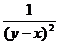 的最简公分母是
的最简公分母是
A.x2一y2 B.(y―x)
4. 计算(1+ )÷(1+
)÷(1+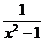 )的结果是
)的结果是
A.1 B.+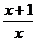 D.
D. 
5.将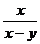 中,
中,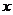 ,
, 都扩大2倍,则分式的值
都扩大2倍,则分式的值
A.不变 B.扩大2倍 C.缩小2倍 D.扩大4倍
6.面积为2的△ABC,一边长为x,这边上的高为y,则Y与x的变化规律用图像表示大致是
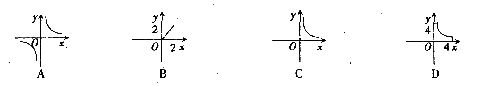
7.函数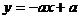 与
与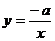 (a≠0)在同一坐标系中的图象可能是
(a≠0)在同一坐标系中的图象可能是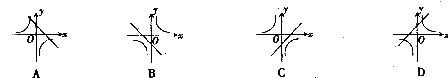
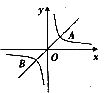
8.在函数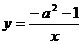 (a为常数)的图象有三点(x1,y1)(x2,y2),(x3,y3)且x1<x2<0<x3,则函数y1,y2,y3的大小关系是
(a为常数)的图象有三点(x1,y1)(x2,y2),(x3,y3)且x1<x2<0<x3,则函数y1,y2,y3的大小关系是
A.y2< y3< y1 B.y3< y2< y3
C.y1 < y2< y3 D.y3 < y1 < y2
9.若△ABC的三边长分别是8,15,17,则最短边上的中线长是
A. B.
B.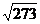 C.
C.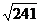 D.以上都不对
D.以上都不对
10.若一直角三角形周长为30,面积为30,则这个直角三角形的斜边长为
A.15 B.
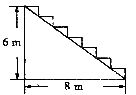
11.艺达宾馆在装修后,准备在大厅的主楼铺设红地毯,已知这种地毯每平方米售价30元,主楼梯道宽
A.1260元 B.900元 C.720元 D.540元
二、填空题(每小题3分,共j3分)
12.当x,y满足关系 时,分式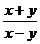 有意义。
有意义。
13.如图,过双曲线y=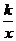 (k>0,x>0)的图象上两点A,B,作AC⊥x轴于C,BD⊥x轴于O,若S △AOC=6,则S△BOD=
.
(k>0,x>0)的图象上两点A,B,作AC⊥x轴于C,BD⊥x轴于O,若S △AOC=6,则S△BOD=
.
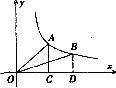
14.如图,直线y=kx(k>0)与双曲线y= 交于A(x1,y1),B(x2,y2)两点, 则2x1y2-7x2y1的值等于
。
交于A(x1,y1),B(x2,y2)两点, 则2x1y2-7x2y1的值等于
。
15.在公式L=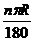 (n≠0)中,用L、n表示R的式子是 .
(n≠0)中,用L、n表示R的式子是 .
16.从家到学校的距离为
象限.
17.已知一次函数y=kx+b的图象经过第一、二、四象限,则反比例函数y= 的图象经过第
的图象经过第
18.反比例函数y=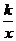 在x=2处自变量增加1,函数值相应地减少了
在x=2处自变量增加1,函数值相应地减少了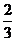 ,则k= .
,则k= .
19.已知菱形ABCD的边长为6,∠A=60°,如果点P是菱形内一点,且PB=PD=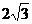 ,那么AP的长为 。
,那么AP的长为 。
20.在△ABC中,∠C=90°,若a:b=3:4,c=10,则a= ,b= .
21.若等腰直角三角形的斜边长为
22.--个容器装有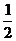 升水,第2次倒出水量是
升水,第2次倒出水量是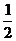 升的
升的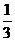 ,第3次倒出水量是
,第3次倒出水量是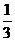 升的
升的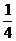 ,第4次倒出水量是
,第4次倒出水量是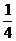 升的
升的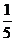 ,……按照这种倒水的方法,10次倒出的水的总量是
,……按照这种倒水的方法,10次倒出的水的总量是
三、解答题:(共34分)
23.(6分)计算:
(1)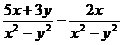
(2) 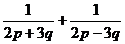
(3)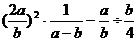
24.(5分)已知: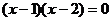 ,求
,求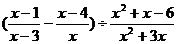 的值.
的值.
25.“丰收l号”小麦的试验田是边长为a米的正方形减去一个边长为
(1)哪种小麦的单位面积产量高?
(2)高的单位面积产量是低的单位面积产量的多少倍?
26.从2004年5月起某列车平均提速v千米/时,用相同的时间,列车提速前行驶s千米,提速后比提速前多行驶50千米,提速前列车的平均速度为多少?
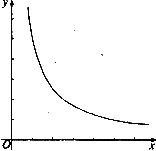
27.如图是反比例函数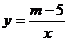 的图象的一支.根据图象回答下列问题:
的图象的一支.根据图象回答下列问题:
(1)图象的另一支在哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(a,b)和B(a′,b′).如果a>a′,那么b和b′有怎样的大小关系?
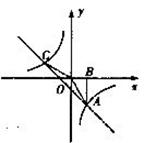
28.如图,Rt△AOB的顶点A是双曲线y=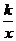 与直线y=-x+(k+1)在第四象限的交点,AB⊥x轴于B,且S△ABO=
与直线y=-x+(k+1)在第四象限的交点,AB⊥x轴于B,且S△ABO=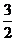 .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com