
2007年济南市市中区高中阶段学校招生模拟考试
九年级数学试题
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页,第Ⅱ卷3至8页,共120分。考试用时l20分钟。
第Ⅰ卷(选择题共48分)
注意事项:
1.数学考试中允许使用不含存储功能的计算器。
2.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。 3.选择题为四选一题目,每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案。不能答在测试卷上。
4.考试结束,监考教师将本试卷和答题卡一并收回。
一、选择题:本大题共l2个小题.每小题4分;共48分.在每小题给出 的四个选项中,只有一项是符合题目要求的。
1.-3的倒数是 ( )
A.一3
B.3 C. D.
D.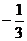
2.下列运算正确的是 ( )
A.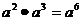 B.
B.
C. D.
D.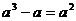
3.班主任为了解学生星期六、日在家的学习情况,家访了班内的六位学生,了解到他们在家的学习时间如下表所示.那么这六位学生学习时间的众数与中位数分别是 ( )
学生姓名
小丽
小明
小颖
小华
小乐
小恩
学习时间
(小时)
4
6
3
4
5
8
A.4小时和4.5小时 B.4.5小时和4小时
C.4小时和3.5小时 D.3.5小时和4小时
4.据“保护长江万里行”考察队统计,仅2006年长江流域废水排放量已达163.9亿吨!治长 江污染真是刻不容缓了!请将这个数据用四舍五入法,使其保留两个有效数字,再用科学记数法表示出来是 ( )
(A) 亿吨 (B)
亿吨 (B) 亿吨 (C)
亿吨 (C) 亿吨 (D)
亿吨 (D) 亿吨
亿吨
5.如图,水杯的俯视图是 ( )

6.已知圆锥侧面展开图的圆心角为 ,则该圆锥的底面半径与母线长的比为 ( ) A.1:2
B.2:1 C.1:4 D.4:1
,则该圆锥的底面半径与母线长的比为 ( ) A.1:2
B.2:1 C.1:4 D.4:1
7.在两根相距6米的木杆上系一根绳子,并在绳子上挂上一盏灯,则灯与两杆距离都大于2米的概率是 ( )
A. B.
B. C.
C.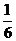 D.
D.
8.如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于 ( )

A. B.
B. C.
C.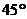 D.
D.
9.若关于 的方程
的方程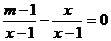 有增根,则
有增根,则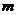 的值是
( )
的值是
( )
A 2 B.3 C.1 D.一l
10.如图,一个蓄水桶,60分钟可将一满桶水放干.其中,水位 随着放水时间
随着放水时间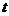 (分)的变化而变化.
(分)的变化而变化. 与
与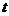 的函数的大致图像为 ( )
的函数的大致图像为 ( )

11.如图,⊙O是△ABC的内切圆,切点分别是D、E、F,已知∠A= ,∠C=
,∠C= ,则∠DFE的度数是
( )
,则∠DFE的度数是
( )

A.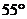 B.
B. C.
C. D.
D.
12.老师出示了小黑板上的题后(如图),小华说:过点(3,0);小彬说:过点(4,3);小明说: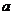 =1;小颖说:抛物线被
=1;小颖说:抛物线被 轴截得的线段长为2。你认为四人的说法中,正确的有 ( )
轴截得的线段长为2。你认为四人的说法中,正确的有 ( )

A.4个 B.3个 C.2个 D.1个
第Ⅱ卷(非选择题共72分)
注意事项:
1.第Ⅱ卷共6页,用蓝、黑钢笔或圆珠笔直接答在试卷上.
2.答卷前将密封线内的项目填写清楚.
二、填空题:本大题共5个小题,每小题3分,共15分,把答案填在题中横线上。
13.请你写出一个比 大的负无理数______________
大的负无理数______________
14.分解因式: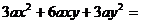 ___________
___________
15.计算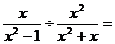 ______________
______________
16. 如图,直线 与
与 轴交于点A,与直线
轴交于点A,与直线 交于点B,且直线
交于点B,且直线 与
与 轴交于点C,则△ABC的面积为___________
轴交于点C,则△ABC的面积为___________

17.小宇同学在一次手工制作活动中,先把一张矩形纸片按图1的方式进行折叠,使折痕的左侧部分比右侧部分短lcm;展开后按图2的方式再折叠一次,使第二次折痕的左侧.部分比右侧部分长lcm,再展开后,在纸上形成的两条折痕之间的距离是________cm

三.解答题:本大题共7个小题,共57分.解答应写出文字说明,证明过程或演算步骤.
18.(本题满分7分)
(1)
(2)
19.(本题满分7分)
(1)已知:如图,平行四边形ABCD中,BD是对角线,AE⊥BD于E,CF⊥BD于F.
求证:BE=DF.

(2)如图,某一时刻太阳光从教室窗户射入室内,与地面的夹角∠BPC为 ,窗户的一部分在教室地面所形成的影长PE为3.5米,窗户的高度AF为2.5米。求窗外遮阳蓬外端一点D到窗户上椽的距离AD.(结果精确到0.1米)
,窗户的一部分在教室地面所形成的影长PE为3.5米,窗户的高度AF为2.5米。求窗外遮阳蓬外端一点D到窗户上椽的距离AD.(结果精确到0.1米)

20.(本题满分8分)
(1)解方程: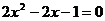
(2)解不等式组
21.(本题满分8分)
一枚均匀的正方体骰子,六个面分别标有数字l,2,3,4,5,6,连续抛掷两次,朝上的数字分别是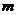 ,
,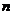 作为点A的横、纵坐标,那么点A(
作为点A的横、纵坐标,那么点A(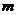 ,
,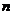 )在函数
)在函数 的图像上的概率是多少?
的图像上的概率是多少?
22.(本题满分9分)
某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加l0件.
(1) 求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价 元,商场一天可获利润
元,商场一天可获利润 元.
元.
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出 与
与 之间的函数关系式,并通过画该函数图像的草图,观察其图像的变化趋势,结合题意写出当
之间的函数关系式,并通过画该函数图像的草图,观察其图像的变化趋势,结合题意写出当 取何值时,商场获利润不少于2160元?
取何值时,商场获利润不少于2160元?
23.(本题满分9分)
如图,已知直线 与抛物线
与抛物线 交于A、B两点.
交于A、B两点.
(1)求A、B两点的坐标;
(2)求线段AB的垂直平分线的解析式;
(3)如图,取与线段AB等长的一根橡皮筋,端点分别固定在A、B两处.用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A、B构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时P点的坐标;如果不存在,请简要说明理由.


24.(本题满分9分)
如图,在平面直角坐标系中,直线 分别交
分别交 轴
轴 轴于A、B亮点.
轴于A、B亮点.
(1)求A、B两点坐标;
(2)设P是直线AB上一动点(点P与点A不重合),⊙P始终和 的轴相切,和直线AB交于C、D两点(点C的横坐标小于点D的横坐标),设P点的横坐标为
的轴相切,和直线AB交于C、D两点(点C的横坐标小于点D的横坐标),设P点的横坐标为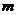 ,试用含有
,试用含有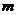 的代数式表示C点的横坐标;
的代数式表示C点的横坐标;
(3)在(2)的条件下,若点C在线段AB上,求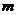 为何值时,△BOC为等腰三角形.
为何值时,△BOC为等腰三角形.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com