
2007年日照市初中毕业生学业水平测试(大纲卷)
数学试卷
温馨提示:1.本试卷满分100分,考试时间100分钟,请合理利用时间。
2.本试卷分为卷I选择题和卷Ⅱ综合题。
3.请把答案写到相应位置,字迹工整,条理清晰。
第Ⅰ卷 选择题(总分30分)
一、选择题:本题中有10小题,每小题3分,共30分。每题给出的四个选项中只有一项符合题目要求,请将正确选项代号填入题后括号内。
1.计算: 的结果是( )
的结果是( )
(A) (B)
(B)
 (C)
(C) (D)
(D)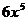
2.下列说法中,正确的是( )
(A)  的系数是
的系数是
(B)在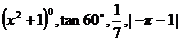 这几个数中,实数有2个
这几个数中,实数有2个
 (C)若
(C)若 则
则
(D)单项式 与单项式
与单项式 不可能是同类项
不可能是同类项
3.如图,梯子的各条横档互相平行,若∠1=110°,则∠2的度数为( )
(A)50° (B)70°
(C)90° (D)110°
4.样本数据10,10, ,8的众数与平均数相同,那么这组数据的中位数是( )
,8的众数与平均数相同,那么这组数据的中位数是( )
(A)12 (B)lO (C)9 (D)8
5.关于 的不等式
的不等式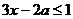 的解集如图所示,则a的值为( )
的解集如图所示,则a的值为( )
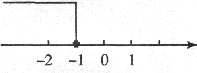
(A)1 (B)-1 (C)2 (D)-2
6.已知圆锥的底面半径为
(A)90° (B)120° (C)240° (D)270°
7.直线 经过第二、三、四象限,那么下列结论正确的是( )
经过第二、三、四象限,那么下列结论正确的是( )
(A)
(B)点 在第一象限内
在第一象限内
(C)反比例函数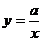 当
当 >O时函数值随
>O时函数值随 的增大而减小
的增大而减小
(D)抛物线 的对称轴过二、三象限
的对称轴过二、三象限
8.如图:AB是⊙O的直径,CD是弦,若AB=
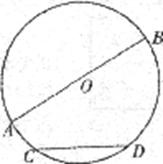
(A)
9. 若弹簧的总长度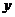 (cm)是所挂重物
(cm)是所挂重物 (千克)的一次函数,图象如图所示,由图可知,不挂重物时,弹簧的长度是( )
(千克)的一次函数,图象如图所示,由图可知,不挂重物时,弹簧的长度是( )
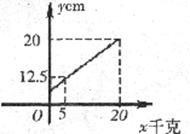
(A)
10.如图所示为信息联网工程,小圆圈表示网络的结点,结点之间的连线标注的数字表示该段网线单位时间内可以通过的最大的信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )

(A)15 (B)20 (C)54 (D)64
第Ⅱ卷 综合分析题(共12小题 总分70分)
二、填空题:本题中有5小题,每小题3分,共15分.请将答案直接填在题中的横线上.
11.据“保护长江万里行”考察队统计,长江流域废水排放量每年已达163.9亿吨!治理长江污染真是刻不容缓了!请将163.9亿吨这个数据保留两个有效数字,并用科学记数法表示是 吨.
12.如图,是用4个全等的等腰梯形镶嵌成的图形,则这个图形中等腰梯形上、下两底的比是 .

13.一元二次方程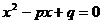 的两根分别为1和2,那么将
的两根分别为1和2,那么将 因式分解的结果为 .
因式分解的结果为 .
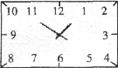
14.如图,是长方形时钟钟面示意图,时钟的中心在长方形对角线的交点上,长方形的宽为
15.如图,△ 都是等腰直角三角形,点
都是等腰直角三角形,点 在函数
在函数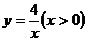 的图象上,斜边
的图象上,斜边 都在
都在 轴上,则点
轴上,则点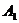 的坐标是 ,点
的坐标是 ,点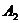 的坐标是
,点
的坐标是
,点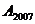 的坐标是 .
的坐标是 .

三、解答题:本题中有7小题,共55分.解答时应写出文字说明、证明过程或推演步骤.
16.(本题满分5分)
化简:
17.(本题满分7分)
“五一”旅游黄金周期间,几名同学包租一辆面包车前往“浮来山”游玩,面包车的租价为180元,出发时又增加了几名学生,实际参加游玩的学生数是原来准备参加游玩的学生数的1.2倍,结果每个同学比原来少分担3元车费,求实际参加游玩的同学数是多少?
18.(本题满分7分)
如图,在梯形ABCD中,AD//BC,AB=DC=AD,∠ADC=120°.

(1)求证:BD⊥DC;
(2)若AB=4,求梯形ABCD的面积.
19.(本题满分8分)
甲、乙两个商场在同一周内经营同一种商品,每天的获利情况如下表:
日期
星期一
星期二
星期三
星期四
星期五
星期六
星期日
甲商场获利/万元
2.5
2.4
2.8
3
3.2
3.5
3.6
乙商场获利/万元
1.9
2.3
2.7
2.6
3
4
4.5
(1)请你计算出这两个商场在这周内每天获利的平均数.
(2)在图中所示的网格图内画出两个商场每天获利的折线图;(甲商场用虚线,乙商场用实线)
(3)根据折线图请你预测下周一哪个商场的获利会多一些?并简单说出你的理由.

20.(本题满分8分)
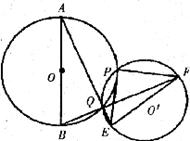
如图,AB为⊙O的直径,P为AB弧的中点,⊙O'为过点P的圆,与⊙O相交于点Q,连接AQ、BQ并延长分别交⊙O'于点E、F,请判断△PEF的形状,并证明你的结论.
21.(本题满分10分)
某工厂生产某种产品,每件产品的出厂价为1万元,其原材料成本价(含设备损耗等)为0.55万元,同时在生产过程中平均每生产一件产品有1吨的废渣产生.为达到国家环保要求,需要对废渣进行脱硫、脱氮等处理,现有两种方案可供选择:
方案二、工厂将废渣集中到废渣处理厂统一处理,每处理1吨废渣需付O.1万元的处理费.
问:(1)设工厂每月生产 件产品,每月利润为
件产品,每月利润为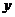 万元,分别求出方案一和方案二处理废渣时,
万元,分别求出方案一和方案二处理废渣时,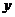 与
与 之间的函数关系式(利润=总收入一总支出);
之间的函数关系式(利润=总收入一总支出);
(2)若你作为工厂负责人,如何根据月生产量选择处理方案,既可达到环保要求又最合算.
22.(本题满分10分)
如图,A(O,1)是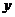 轴上一定点,B是
轴上一定点,B是 轴上一动点,以AB为边,在∠OAB的外部作∠BAE=∠OAB,过B作BC⊥AB,交AE于点C.
轴上一动点,以AB为边,在∠OAB的外部作∠BAE=∠OAB,过B作BC⊥AB,交AE于点C.
(1)当点B在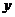 轴上运动时,设点C的纵、横坐标分别为
轴上运动时,设点C的纵、横坐标分别为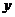 、
、 ,试求
,试求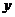 与
与 的函数关系式(当点B运动到O点时,点C也与0点重合);
的函数关系式(当点B运动到O点时,点C也与0点重合);
(2)设过点P(O,-1)的直线L与(2)中所求函数的图象有两个公共点 ,求直线L的解析式.
,求直线L的解析式.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com