1．下面是一名同学所做的5道练习题：①；②；③；④；⑤；他做对的题数是（    ）

A．0    B．1    C．2    D．3

2．世界文化遗产长城的总长度约为670 000m，用科学记数法表示为（    ）

A．    B．    C．    D．

3．关于的一元二次方程的一个根是0，则的值为（    ）

A．1    B．0    C．―1    D．±1

4．用两块边长为a的等边三角形纸片拼成的四边形是(    )

A．等腰梯形    B．正方形    C．矩形    D．菱形

5．如果用□表示1个立方体，用表示两个立方体重叠，用表示三个立方体重叠，那么，如图1，是由7个立方体叠成的几何体，从正前方观察，可画出的平面图形是（    ）

6．因式分解：=_________________________．

7．函数中自变量的取值范围是____________________________．

8．图2是一组数据的折线统计图，这组数据的极差是_________，平均数约是_______．（保留到整数位）

9、将矩形ABCD沿AE折叠，得到如图3所示的图形，已知∠CED=60°，则∠EAD=______．

10．用一张面积为8πcm的扇形，纸张卷成一个如图4所示的圆锥，已知圆锥的母线是底面半径的两倍，则圆锥底面半径是__________．

11．

12．老师布置了一道计算题：计算的值，其中a=2006，b=2007，小明把a、b错抄成a=2007，b=2006，但老师发现他的答案还是正确的，你认为这是怎么回事？说说你的理由．

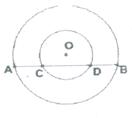
13、如图5，两圆都以点O为圆心，直线分别交两园A、B两点和C、D两点，请你找出线段AC和BD的数量关系，并证明你的结论。

14、有一个抛两枚硬币的游戏，规则是：若出现两个正面，则甲赢；若出现一正一反，则乙赢；若出现两个反面，则甲、乙都不赢。

（1）这个游戏是否公平？请说明理由；

（2）如果你认为这个游戏不公平，那么请你改变游戏规则，设计一个公平的游戏；如果你认为这个游戏公平，那么请你改变游戏规则，设计一个不公平的游戏。

15、如图所示，请你用三种方法，把左边的小正方形分别平移到右边三个图形中，使各个图形成为轴对称图形，并分别画出其对称轴所在的位置。

16、如图，某公司入口处原有三级台阶，每级台阶高为20cm，深为30cm，为方便残疾人士，拟将台阶改成斜坡，高台阶的起点为A，斜坡的起始点为C（如图所示），现将斜坡的坡角∠BCA设计为12°，那么斜坡起点C应离A点多远？（精确到1cm，sin12°=0.208，cos12°=0.978，tan12°=0.213）

17、某校初二年级全体320名学生，在电脑培训前后各参加了一次水平相同的考试，考分都以同一标准划分成“不及格”、“及格”、“优秀”三个等级，为了了解电脑培训的效果，用抽签方式得到其中32名学生的两次考试考分等级，所绘制的统计图如图所示，试结合图形信息回答下列问题：

（1）这32名学生培训前考分的中位数所在的等级是______________，培训后考分的中位数所在的等级是__________________．

（2）这32名学生经过培训，考分等级“不合格”的百分比由__________下降到________．

(3)估计该校整个初二年级中，培训后考分等级为“合格”与“优秀”的学生共有_______名．

（4）你认为上述估计合理吗？理由是什么？

答：________________，理由是___________________________________________．

18．某校七年级在学校团委的组织下，围绕“八荣八耻”开展了一次知识竞赛活动，竞赛规则：每班代表队都必须回答27道题，答对一题得5分，答错或不答都倒扣1分。

（1）在比赛到第18题结束时，（3）班代表队得分为78分，这时（3）班答对了多少道题？

（2）比赛规定，只有得分超过100分（含100分）时才能获奖。在第（1）小题的条件下，（3）班代表队在后面的比赛中至少还要答对多少题才有可能获奖？请简要说明理由．

19．如图所示，在⊙O中，AB是直径，半径为r，弧AB=，

求：（1）∠AOC的度数；

（2）若D为弧BC上一动点，且AD与半径OC交于点E，当D在什么位置时，△AEC≌△EDO．

五、解答题(每题9分，共27分)

20．如图（a），已知AB是⊙O的直径，CB是⊙O的切线，B为切点，D是⊙O上一点（不A、B重合）

（1）求证：∠DAB=∠DBC．

（2）若AB不是⊙O的直径，其它条件不变，（1）中的结论还成立吗？若成立则给出你的证明；若不成立，请说明理由．

21．某公司试销一种成本单价为500元/件的新产品，规定试销时的销售单价不低于成本单价，又不高于800元/件，经试销调查发现销售量（件）与销售单价（元/件）可近似看作一次函数的关系（如图所示）．

(1)根据图象，求一次函数的表达式；

(2)设公司获得毛利润（毛利润=销售总价―成本总价）为S元．①试用销售单价表示毛利润S；②试问销售单价定为多少时，该公司获得最大毛利润？最大毛利润是多少？此时的销售量是多少？

22．如图所示，在平面直角坐标系中，正方形ABCD的边长为4，点B在系原点上，P是BC上一动点，QP⊥AP交DC于Q，设PB=，△ADQ的面积为．

(1)求与之间的函数关系式，并写出自变量的取值范围．

(2) (1)中函数若是一次函数，求出直线与两坐标轴围成的三角形面积，若是二次函数，请利用配方法求出抛物线的对称轴和顶点坐标．

(3)点P是否存在这样的位置，使△APB的面积是△ADQ的面积的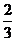，若存在，求出点P的坐标，若不存在，请说明理由．