
2007年北京海淀区初三下学期期中练习数学试卷
满分120分,考试时间120分钟。
一、选择题(本题共32分,每小题4分。)
1.4的平方根等于
A. B.-
B.-
2.据报道,在“十一五”期间,我国民用航天工作排在首位的大事是做好月球探测工程的研制工作,确保2007年飞行成功。已知月球与地球的距离约为
A. B.
B.
C. D.
D.
3.在函数 中,自变量x的取值范围是
中,自变量x的取值范围是
A. B.
B.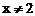 C.
C.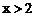 D.
D.
4.如图1,在△ABC中,∠C=90°,BC=3,AB=5,则下列结论正确的是
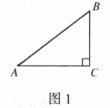
A. B.
B. C.
C. D.
D.
5.一个口袋中放着8个红球和16个黑球,这两种球除了颜色以外没有任何区别。袋中的球已经搅匀。从口袋中任取一个球,这个球是红球的概率为
A. B.
B. C.
C. D.
D.
6.如图2,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=125°,则∠DBC的度数为

A.55° B.65° C.75° D.125°
7.图3是一个电脑桌面背景图,左右两个“京”字图的面积比约是

A.2:1 B.4:
8.科技馆为某机器人编制一段程序,如果机器人在平地上按照图4中的步骤行走,那么该机器人所走的总路程为
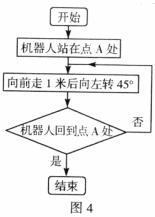
A.
二、填空题(本题共16分,每小题4分。)
9.已知关于x的方程 有两个不相等的实数根,则m的取值范围是________。
有两个不相等的实数根,则m的取值范围是________。
10.若实数p、q满足 ,则
,则 的值为_____________。
的值为_____________。
11.甲、乙两人进行射击比赛,在相同条件下各射击10次。他们的平均成绩均为7环,10次射击成绩的方差分别是 ,则成绩较为稳定的是____________。(填“甲”或“乙”)
,则成绩较为稳定的是____________。(填“甲”或“乙”)
12.如图5,小明将一块边长为 的正方形纸片折叠成领带形状,其中
的正方形纸片折叠成领带形状,其中 ,B点落在CF边上的
,B点落在CF边上的 处,则
处,则 的长为______________。
的长为______________。

三、解答题(本题共30分,每小题5分。)
13.计算: 。
。
14.解不等式组: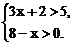
15.已知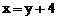 ,求代数式
,求代数式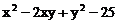 的值。
的值。
16.解方程:
17.已知:如图6,在△ABC中,∠ABC=90°。以点C为圆心,AC长为半径画弧,点D为圆弧上一点,且∠ACD=90°,过点D作直线BC的垂线DF,垂足为F。求证: 。
。

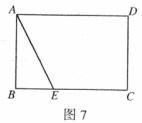
18.如图7,在矩形ABCD中, 点E为BC边上一点,且
点E为BC边上一点,且 ,求点D到AE的距离。
,求点D到AE的距离。
四、解答题(本题共20分,每小题5分。)
19.图8-①是北京市

(1)根据图8-①提供的信息,在图8-②中补全频数分布直方图;
(2)这10天的最低气温的众数是___________℃,中位数是___________℃,平均数是___________℃。
20.如图9,线段AB经过圆心O,交⊙O于A、C两点,点D在⊙O上,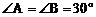 。
。
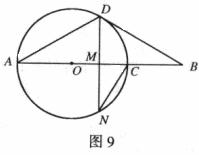
(1)求证:BD是⊙O的切线;
(2)若点N在⊙O上,且DN⊥AB,垂足为M,NC=10,求AD的长。
21.如图10,一次函数 的图象与反比例函数
的图象与反比例函数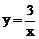 的图象相交于A、B两点。
的图象相交于A、B两点。
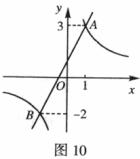
(1)利用图象中的信息,求一次函数的解析式;
(2)已知点 在一次函数的图象上,点
在一次函数的图象上,点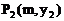 在反比函数的图象上。当
在反比函数的图象上。当 时,直接写出m的取值范围。
时,直接写出m的取值范围。
22.已知:p为实数。

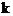

…
…
…
3


4
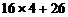

5


6


7
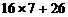

…
…
…
根据上表中的规律,回答下列问题:
(1)当p为何值时, ?
?
(2)当p为何值时,k与q的值相等?
五、解答题(本题共22分,第23题6分,第24题8分,第25题8分。)

探究1:当我们把半径为 (间隙如图11所示),求
(间隙如图11所示),求 的长;(
的长;(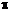 取3.14,结果精确到
取3.14,结果精确到
探究2:将探究1中的足球分别换成乒乓球和地球,其他条件都不改变。设乒乓球的半径为r,细线与乒乓球表面的间隙为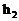 ;地球的半径为R,细线与地球表面的间隙为
;地球的半径为R,细线与地球表面的间隙为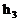 ,试比较
,试比较 的大小,并说明理由。
的大小,并说明理由。
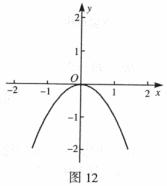
24.已知,如图12,在平面直角坐标系 中,抛物线
中,抛物线 的解析式为
的解析式为 ,将抛物线
,将抛物线 平移后得到抛线物
平移后得到抛线物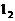 ,若抛物线
,若抛物线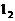 经过点(0,2),且其顶点A的横坐标为最小正整数。
经过点(0,2),且其顶点A的横坐标为最小正整数。
(1)求抛物线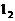 的解析式;
的解析式;
(2)说明将抛物线 如何平移得到抛物线
如何平移得到抛物线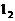 ;
;
(3)若将抛物线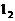 沿其对称轴继续上下平移,得到抛物线
沿其对称轴继续上下平移,得到抛物线 ,设抛物线
,设抛物线 的顶点为B,直线OB与抛物线
的顶点为B,直线OB与抛物线 的另一个交点为C。当
的另一个交点为C。当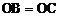 时,求点C的坐标。
时,求点C的坐标。
25.如图13,在平面直角坐标系 中,直线
中,直线 分别交x轴、y轴于C、A两点。将射线AM绕着点A顺时针旋转45°得到射线AN。点D为AM上的动点,点B为AN上的动点,点C在∠MAN的内部。
分别交x轴、y轴于C、A两点。将射线AM绕着点A顺时针旋转45°得到射线AN。点D为AM上的动点,点B为AN上的动点,点C在∠MAN的内部。

(1)求线段AC的长;
(2)当 轴,且四边形ABCD为梯形时,求△BCD的面积;
轴,且四边形ABCD为梯形时,求△BCD的面积;
(3)求△BCD周长的最小值;
(4)当△BCD的周长取得最小值,且 时,△BCD的面积为_____________。
时,△BCD的面积为_____________。
(第(4)问只需填写结论,不要求书写过程)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com