
2007年北京市宣武区初三下学期第一次质量检测
数学试卷2007.5
第I卷(选择题 共32分)
一、选择题(共8个小题,每小题4分,共32分)下列各题均有四个选项,其中只有一个是符合题目要求的。
1.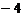 的绝对值是( )
的绝对值是( )
A.4 B.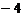 C.2 D.
C.2 D.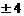
2.已知△ABC∽△DEF,AB:DE=1:2,则△ABC与△DEF的周长比等于( )
A.2:1 B.4:
3.如果要用正三角形和正方形两种图形镶嵌平面,那么至少需要( )
A.三个正三角形,三个正方形 B.两个正三角形,三个正方形
C.两个正三角形,两个正方形 D.三个正三角形,两个正方形
4.如图所示几何体的左视图是( )
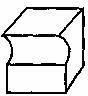
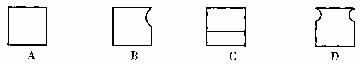
5.有一个数值转换器,原理如下:

当输入的x为64时,输出的y是( )
A.8 B.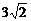 C.
C.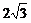 D.
D.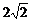
6.甲、乙两户居民家庭全年各项支出的统计图如下:
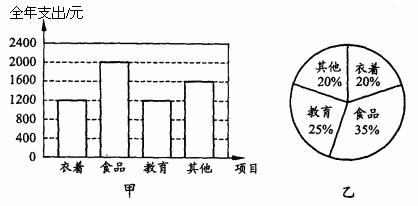
根据统计图,下列对两户教育支出占全年总支出的百分比作出的判断中,正确的是( )
A.乙户比甲户大 B.甲户比乙户大
C.甲、乙两户一样大 D.无法确定哪一户大
7.某农场租用收割机收割小麦,甲收割机单独收割2天后,又调来乙收割机参与收割,直至完成800亩的收割任务,收割亩数与天数之间的函数关系如图所示,那么乙参与收割的天数是( )
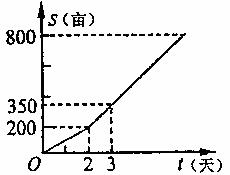
A.3天 B.4天 C.5天 D.6天
8.如图,将一张矩形纸对折再对折,然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是( )
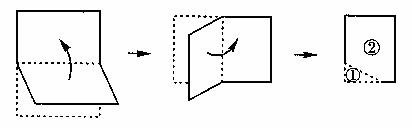
A.矩形 B.三角形 C.菱形 D.梯形
第II卷(非选择题 共88分)
二、填空题(共4个小题,每小题4分,共16分)
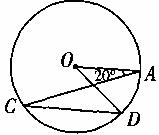
9.如图,在⊙O中,已知∠OAC=20°,OA//CD,则∠AOD=_____________。
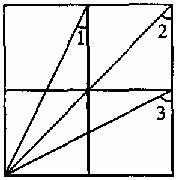
10.如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3=_____________。
11.在不透明的袋中装有仅颜色不同的一个红球和一个蓝球,从此袋中随机摸出一个小球,然后放回,再随机摸出一个小球,则第一次摸出红球,第二次摸出蓝球的概率是_____________。
12.已知一列数,1,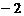 ,3,
,3,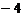 ,5,
,5,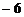 ,7,…
,7,…
将这列数排成下列形式:
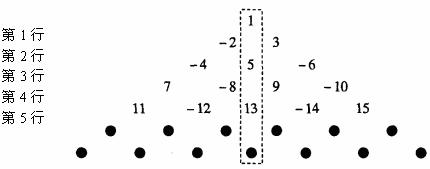
中间用虚线围的一列数,从上至下依次为1、5、13、25、……,按照上述规律排下去,那么虚线框中的第7个数是_____________。
三、解答题:(共5个小题,每小题4分,共20分)
13.计算: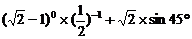 。
。
14.解方程: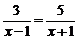 。
。
15.解不等式组: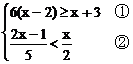
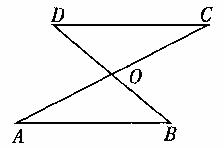
16.如图,AC交BD于点O,请你从下面三项中选出两个作为条件,另一个为结论,写出一个真命题,并加以证明。
(1)OA=OC
(2)OB=OD
(3)AB//DC
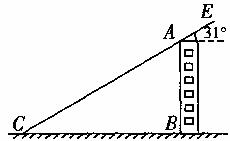
17.某地某时刻太阳光线与水平线的夹角为31°,此时在该地测得一幢楼房在水平地面上的影长为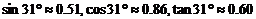 )
)
四、解答题(共3个小题,每小题5分,共15分)
18.在日常生活中如取款、上网等都需要密码。有一种用“因式分解”法产生的密码,方便记忆。原理是:如对于多项式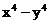 ,因式分解的结果是
,因式分解的结果是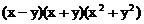 ,若取
,若取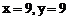 时,则各个因式的值是:
时,则各个因式的值是: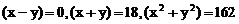 ,于是就可以把“
,于是就可以把“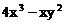 ,取x=10,y=10时,写出一个用上述方法产生的密码,并说明理由。
,取x=10,y=10时,写出一个用上述方法产生的密码,并说明理由。
19.△ABC和△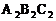 在方格纸中的位置如图所示。
在方格纸中的位置如图所示。
(1)将△ABC向下平移4格得到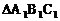 ,画出
,画出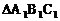 ;
;
(2)请在方格纸中建立直角坐标系,使得A、B两点的坐标分别为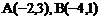 ,并写出C点坐标;
,并写出C点坐标;
(3)请将△ABC变换到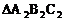 的过程描述出来。
的过程描述出来。
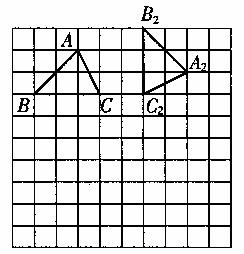
20.已知:∠MAN=30°,O为边AN上一点,以O为圆心、2为半径作⊙O,交AN于D、E两点,设AD=x。
(1)如图1,当⊙O与AM相切于点F时,求x的值;
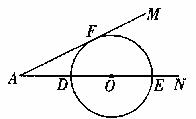
图1
(2)如图2,当⊙O与AM相交于B、C两点,且∠BOC=90°时,求x的值。
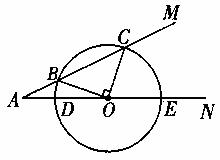
图2
五、解答题(共2个小题,每小题6分,共12分)
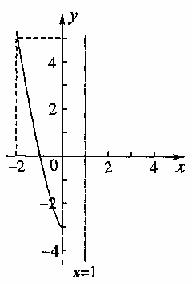
21.已知二次函数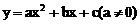 的图象与y轴相交于点
的图象与y轴相交于点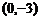 ,并经过点
,并经过点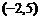 ,它的对称轴是x=1,如图为函数图象的一部分。
,它的对称轴是x=1,如图为函数图象的一部分。
(1)求函数解析式,写出函数图象的顶点坐标;
(2)在原题图上,画出函数图象的其余部分;
(3)如果点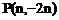 在上述二次函数的图象上,求n的值。
在上述二次函数的图象上,求n的值。
22.某市《居住区供配电设施建设标准》规定,住房面积在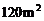 及以下的居民住宅,用电的基本配置容量(电表的最大功率)应为8千瓦。为了了解某区该类住户家用电器总功率情况,有关部门从中随机调查了50户居民,所得数据(均取整数)如下:
及以下的居民住宅,用电的基本配置容量(电表的最大功率)应为8千瓦。为了了解某区该类住户家用电器总功率情况,有关部门从中随机调查了50户居民,所得数据(均取整数)如下:
家用电器总功率(单位:千瓦)
2
3
4
5
6
7
户数
2
4
8
12
16
8
(1)这50户居民的家用电器总功率的众数是___________千瓦,中位数是___________千瓦;
(2)若该区这类居民约有2万户,请你估计这2万户居民家用电器总功率的平均值;
(3)若这2万户居民原来用电的基本配置容量都为5千瓦,现市供电部门拟对家用电器总功率已超过5千瓦用户的电表首批增容,改造为8千瓦,请计算该区首批增容的用户约有多少户?
六、解答题(共3个小题,第23题7分,第24题8分,第25题10分,共25分)
23.某商店经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克,销售单价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况请解答以下问题:
(1)当销售单价定为每千克55元时,计算月销售量和月销售利润;
(2)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
24.已知直线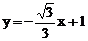 与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°,点
与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°,点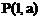 为坐标系中的一个动点。
为坐标系中的一个动点。
(1)求△ABC的面积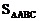 ;
;
(2)证明:不论a取任何实数,△BOP的面积是一个常数;
(3)要使得△ABC和△ABP的面积相等,求实数a的值。
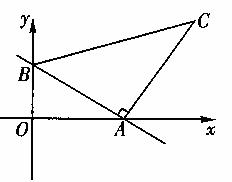
25.如图1,△ACB≌△DCE,其中∠ACB=∠DCE=90°,AC=4,BC=2,点D、C、B在同一条直线上,点E在边AC上。
图1
(1)直线DE与AB有怎样的位置关系?请证明你的结论;
(2)如图2,△DCE沿着直线DB向右平移,若点E恰好落在边AB上,求平移距离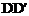 ;
;
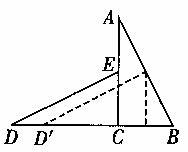
图2
(3)在△DCE沿着直线DB向右平移的过程中,当△DCE与△ACB的公共部分是四边形时,设平移过程中的平移距离为x,这个四边形的面积为y,求y与x的函数关系式,并写出x的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com