
2007年枣庄市滕州七年级数学试题
一、选择题(每小题3分,共36分)
1.下列运算,正确的是
A.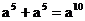 B.
B.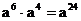
C.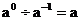 D.
D.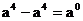
2.下列计算,错误的是
A.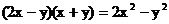
B.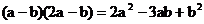
C.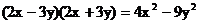
D.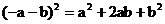
3.某种奖券的中奖率是l%,小花买了100张奖券,下列说法正确的是
A.小花一定会中奖 B.小花一定不中奖
C.小花中奖的可能性较大 D.小花中奖的可能性很小
4.有两根木棒,它们的长分别为
A.
5.如下图所示,一束光线垂直照射水平地面,在地面上放一个平面镜,欲使这束光线经过平面镜反射后成水平光线,则平面镜与地面所成的锐角的度数为
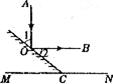
A.45° B.60° C.75° D.80°
6.下列命题:(1)相等的角是对顶角;(2)同位角相等;(3)直角三角形的两个锐角互余;(4)若两条线段不相交,则这两条线段平行。其中,正确命题的个数为
A.l个 B.2个 C.3个 D.4个
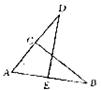
7.如图, 的依据是
的依据是
A.ASA B.AAS C.SAS D.SSS
8.如图, 是直角三角形,且
是直角三角形,且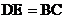 ,以D、E为顶点,做出位置不同的三角形,使所作的三角形与
,以D、E为顶点,做出位置不同的三角形,使所作的三角形与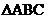 全等,则这样的三角形一共可以做出
全等,则这样的三角形一共可以做出
A.2个 B.4个 C.5个 D.6个
9.如图,L甲、L乙分别表示甲、乙两名运动员在自行车比赛中所走路程与时间的关系,则它们的平均速度的关系是
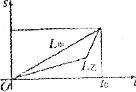
A.甲比乙快 B.乙比甲快 C.甲、乙同速 D.不一定
10.某人账户存款a元,每月支出b元,收入c元(b<a),则账户余额与月份的之间的关系是下列图中的
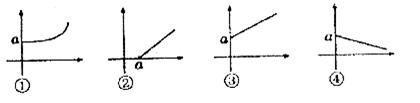
A.① B.②和③ C.③和④ D.③
11.如图,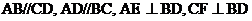 垂足分别为E、F两点,则图中全等的三角形有
垂足分别为E、F两点,则图中全等的三角形有

A.1对 B.2对 C.3对 D.4对
12.在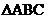 和
和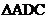 ,有下列三个论断:(1)
,有下列三个论断:(1)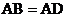 ,(2)
,(2)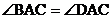 ,(3)
,(3)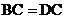 。将两个论断作为条件,另一个论断作为结论构成三个命题:
。将两个论断作为条件,另一个论断作为结论构成三个命题:
(1)若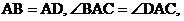 则
则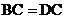 ;
;
(2)若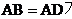
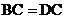 ,则
,则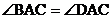 ;
;
(3)若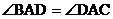 ,
,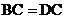 ,则
,则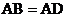 ;
;
其中,正确命题的个数为
A.l个 B.2个 C.3个 D.0个
二、填空题:(每小题4分,共24分,答案填在题中横线中。)
13.1纳米=0.
14.制作矩形门框时,常常在其相邻两边上钉上一根木条,这样做的目的是 ,涉及的数学道理是 。
15.一个三角形两边的长分别是质数2和5,若第三边的长也是个质数,那么第三边的长是 。
16.如图,在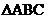 ,
,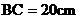 ,AD是
,AD是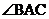 的平分线,BD:CD=2:3,则点D到AC边的距离是
。
的平分线,BD:CD=2:3,则点D到AC边的距离是
。

17.如图,要得到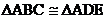 ,除公共角
,除公共角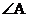 外,在下列横线上写出还需要具备的两个条件,并在括号内写出这些条件得到两个三角形全等的理由。
外,在下列横线上写出还需要具备的两个条件,并在括号内写出这些条件得到两个三角形全等的理由。
(1)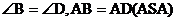
(2) , ( )
18.如图,长方形 的四个顶点在互相平行的两条直线上,AD=
的四个顶点在互相平行的两条直线上,AD=
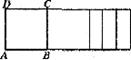
(1)如果设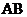 的长为
的长为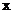 (cm),长方形
(cm),长方形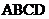 面积为
面积为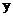 (cm2),则可以表示为
;
(cm2),则可以表示为
;
(2)当长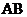 从
从
三、解答题:本大题共7小题,满分60分。
19.(本题满分8分)
利用你所学的知识判断: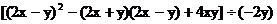 的值与字母
的值与字母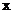 、
、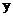 的取值是否有关?
的取值是否有关?
20.(本题满分8分)
如图,C、D、E在同一直线上,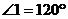 ,
,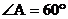 ,直线
,直线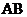 与
与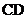 平行吗?请补全所空内容。
平行吗?请补全所空内容。
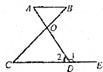
解:直线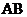 与
与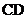 平行。
平行。
因为C、D、E在同一直线上,所以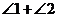 =
。
=
。
因为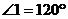 ,所以
,所以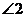 =
。
=
。
因为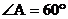 ,所以
,所以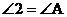
所以 ,理由是 。
21.(本题满分8分)
育人中学初一(1)班学生到野外活动,为测量一池塘两端A、B的距离,设计了如下两种方案:
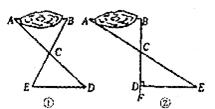
(a)如图①,先在平地上取一个可直接到达 、
、 的点
的点 ,再连结
,再连结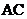 、
、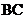 。并分别延长
。并分别延长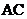 至
至 ,
,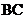 至
至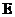 ,使
,使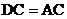 ,
,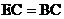 ,最后测出
,最后测出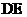 的长即为
的长即为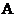 、
、 的距离;
的距离;
22.(本题满分10分)
小明某天上午9时骑自行车离开家,l5时回家,他有意描绘离家的距离与时间的变化情况(如图所示)。
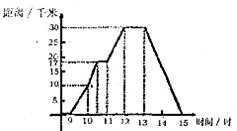
(1)图像表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和l3时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他由离家最远的地方返回的平均速度是多少?
23.(本题满分8分)
如图,在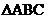 中,
中,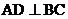 ,
,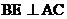 ,垂足分别为
,垂足分别为 、
、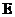 ,AD与
,AD与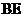 相交于点
相交于点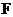 ,若
,若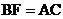 ,求
,求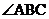 的大小。
的大小。
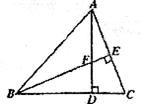
24.(8分)
如图所示,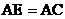 ,
,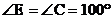 ,
,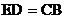 ,
,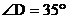 ,
,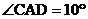 ,求
,求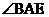 的度数。
的度数。
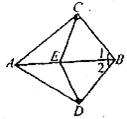
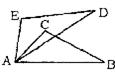
25.(10分)
如图所示,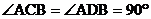 ,
,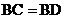 ,
,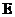 为
为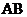 上一点,求证:
上一点,求证: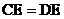 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com