
2007年德州市陵县中考第二次练兵考试
数学试题
(满分:120分,时间:120分钟)
第I卷
一、选择题(本大题共8个小题,每小题3分, 24分,在每小题给出的四个选项中,只有一项是符合题目要求的)。
1.对于任意实数 ,下列各式不一定正确的是( )
,下列各式不一定正确的是( )
A. B.
B.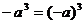 C.
C. D.
D.
2.设 ,
, ,用含
,用含 、
、 的式子表示
的式子表示 ,则下列表示正确的是( )
,则下列表示正确的是( )
A. B.
B. C.
C. D.
D.
3.使式子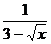 有意义的
有意义的 的值是( )
的值是( )
A. B.
B.
C. D.
D.
4.不等式 的解集是
的解集是 ,则m的取值范围是( )
,则m的取值范围是( )
A.m≤2 8.m≥
 5.一张圆桌旁有四个座位,A先坐在如图所示的座位上,B、C、D三人随机坐到其他三个座位上,则A与B不相邻而坐的概率是( )
5.一张圆桌旁有四个座位,A先坐在如图所示的座位上,B、C、D三人随机坐到其他三个座位上,则A与B不相邻而坐的概率是( )
A. B.
B.
C. D.
D.
6.李大伯承包了一个果园,种植了100棵樱桃树,今年已进入收获期。收获时,从中任选并采摘了l0棵树的樱桃,分别称得每棵树所产樱桃的质量如下表:
序号
l
2
3
4
5
6
7
8
9
10
质量(千克)
14
21
27
17
18
20
19
23
19
22
据调查,市场上今年樱桃的批发价格为每千克l5元。用所学的统计知识估计今年此果园樱桃的总产量与按批发价格销售樱桃所得的总收入分别约为( )
A.200千克,3000元 B.1900千克,28500元
C.2000千克,30000元 D.1850千克,27750元
7.将五边形纸片ABCDE按如图所示的方式折叠,折痕为AF,点E、D分别落在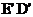 ,已知∠AFC=76º,则
,已知∠AFC=76º,则 等于( )
等于( )
A.3lº B.28º C.24º D.22º


8.已知:如图,动点P在函数 的图像上运动,PM⊥
的图像上运动,PM⊥ 轴于点M,PN⊥
轴于点M,PN⊥ 轴于点N,线段PM、PN分别与直线AB:
轴于点N,线段PM、PN分别与直线AB: 交于点E、F,则AF?BE的值是( )
交于点E、F,则AF?BE的值是( )
A.4 B.2 C.1 D.
 第Ⅱ卷(非选择题 96分)
第Ⅱ卷(非选择题 96分)
二、填空题(本大题共8小题,每小题3分,共24分)
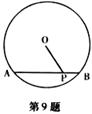
9.已知如图,AB是⊙O的弦、P是AB上的一点,若AB=10cm, PB=4cm,OP=5cm则⊙O的半径是 cm。
10.已知抛物线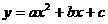 经过点A(-2, 7)、B(6, 7)、C(3, -8),则该抛物线上纵坐标为-8的另一个点的坐标是
。
经过点A(-2, 7)、B(6, 7)、C(3, -8),则该抛物线上纵坐标为-8的另一个点的坐标是
。
 11.已知方程组
11.已知方程组 的解为
的解为 则
则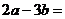 。
。
12.如图,AB是半⊙O的直径,C、D是弧AB的三等分点,如果⊙O的半径为1,P是线段AB上的任意一点,那么图中阴影部分的面积为 。
13.已知菱形ABCD的边长为6,∠A=60º,如果点P是菱形内一点,且PB=PD=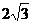 ,那么AP的长为
。
,那么AP的长为
。
14.圆锥的底面半径为6cm,高为8cm,则这个圆锥的侧面展开图的圆心角为 度。
15.如图,O为矩形ABCD的中心,将直角三角板的直角顶点与O点重合转动三角板使两直角边始终与BC、AB相交,交点分别为M、N.如果AB=4,AD=6,OM= ,ON=
,ON= ,则
,则 与
与 的关系式为
。
的关系式为
。


16.如图所示, 、
、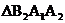 ,是等腰直角三角形,
,是等腰直角三角形, ,点B1、B2在函数
,点B1、B2在函数 (
( )的图像上,斜边
)的图像上,斜边 、
、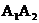 在
在 轴上,则A2的坐标是
。
轴上,则A2的坐标是
。
三、解答题(本大题共8个小题,共72分)
17.(6分)当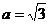 ,
, 时,计算
时,计算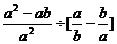 的值。
的值。
 18.(6分)某气象研究中心观测一场沙尘暴从发生到结束的全过程。开始时风速平均每小时增加2千米/时,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米/时。一段时间,风速保持不变,当沙尘暴遇到绿色植被区时,其风速平均每小时减l千米/时,最终停止。结合右侧风速与时间的图像回答下列问题:
18.(6分)某气象研究中心观测一场沙尘暴从发生到结束的全过程。开始时风速平均每小时增加2千米/时,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米/时。一段时间,风速保持不变,当沙尘暴遇到绿色植被区时,其风速平均每小时减l千米/时,最终停止。结合右侧风速与时间的图像回答下列问题:
(1)在 轴( )内填入相应的数值;
轴( )内填入相应的数值;
(2)沙尘暴从发生到结束,共经过 小时;
(3)当 时,风速
时,风速 (千米/时)与时间
(千米/时)与时间 (小时)之间的函数关系式为
。
(小时)之间的函数关系式为
。
19.(满分8分)如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60º,沿山坡向上走到P处再测得点C的仰角为45º,已知PA=100m,山坡的坡度为l∶2且O、A、B在同一条直线上,求电视塔OC的高度以及此人所在位置点 P的铅直高度(结果保留根号形式)。

20.(8分)学习了统计知识后,小刚就本班同学的上学方式进行了一次调查统计。图(1)和图(2)是他通过采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
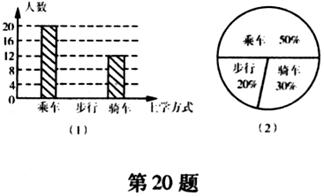
(1)求该班共有多少名学生;
(2)在图(1)中,将表示“步行”的部分补充完整;
(3)在扇形统计图中,计算出“骑车”部分所对应的圆心角的度数;
(4)如果全年级共500名同学,请你估算全年级步行上学的学生人数。
21.(满分l0分)某省公路建设发展速度越来越快,通车总里程已位居全国第一,公路的建设促进了广大城乡客运的发展,某市扩建了市县际公路,运输公司根据实际需要计划买大、中两型客车共l0辆,大型客车每辆为25万元,中型客车每辆15万元。
(1)设购买大型客车 辆,购车总费用为
辆,购车总费用为 万元,求
万元,求 与
与 的函数关系;
的函数关系;
(2)若购车资金为180万元至200万元(含180万元和200万元)那么有几种购车方案?在确保交通安全的前提下,根据客流量调查,大型客车不能少于4辆,此时如何确定购车方案可使该运输公司购车费用最少?
22.(10分)(1)如图a所示,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连结 AD交OC于点E。求证:CD=CE;
(2)若将图a的半径OB所在直线向上平行移动交OA于点F,交
⊙O于点 ,其他条件不变(如图b所示),那么上述结论CD=CE还成立吗?为什么?
,其他条件不变(如图b所示),那么上述结论CD=CE还成立吗?为什么?
(3)若将图a中的半径OB所在直线向上平行移动到⊙O外的CF,点E是DA的延长线与CF的交点,其他条件不变(如图C所示),那么上述结论CD=CE还成立吗?为什么?



23.(12分)某机械租赁公司有同一型号的机械设备40套。经过一段时间的经营发现:当每套机械设备的月租金为270元时,恰好全部租出。在此基础上,当每套设备的月租金每提高l0元时,这种设备就少租出一套,且未租出的一套设备每月需要支出费用(维护费、管理费等)20元。设每套设备的月租金为 (元),租赁公司出租该型号设备的月收益(收益=租金收入-支出费用)为
(元),租赁公司出租该型号设备的月收益(收益=租金收入-支出费用)为 (元)。
(元)。
(1)用含 的代数式表示未租出的设备数(套)以及所有未租出设备(套)的支出费用;
的代数式表示未租出的设备数(套)以及所有未租出设备(套)的支出费用;
(2)求 与
与 之间的二次函数关系式;
之间的二次函数关系式;
(3)当月租金分别为300元和350元时,租赁公司的月收益分别是多少元?此时应该出租多少套机械设备?
(4)请把(2)中所求出的二次函数配方成 的形式,并据此说明:当
的形式,并据此说明:当 为何值时,租赁公司出租该型号设备的月收益最大?最大月收益是多少?
为何值时,租赁公司出租该型号设备的月收益最大?最大月收益是多少?
 24.(12分)如右图,正方形ABCD中,有直径为BC的半圆,BC=2cm,现有E、F两点,分别从B点、A点同时出发,点E沿线段BA以1cm/秒的速度向点A运动,点F沿折线A―D―C以2cm/秒的速度向点C运动,设点E离开B点的时间为t(秒)。
24.(12分)如右图,正方形ABCD中,有直径为BC的半圆,BC=2cm,现有E、F两点,分别从B点、A点同时出发,点E沿线段BA以1cm/秒的速度向点A运动,点F沿折线A―D―C以2cm/秒的速度向点C运动,设点E离开B点的时间为t(秒)。
(1)当t为何值时,线段EF与BC平行?
(2)设l<t<2,当t为何值时,EF与半圆相切?
(3)当1≤t<2时,设EF与AC相交于P点,问E、F运动时,点P的位置是否发生变化?若发生变化,请说明理由;若不发生变化,请给予证明,并求AP∶PC的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com