
2006-2007学年度德州市第二学期期中质量检测
七年级数学试题
一、精心选一选,慧眼识金。(每小题3分,共24分,各小题的四个选项中,有且只有一个是符合题意的,把你认为符合题意的答案选出来,选错或不选或答案超过一个,均记零分)
1、如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )。

A、同位角相等,两直线平行
B、内错角相等,两直线平行
C、同旁内角互补,两直线平行
D、两直线平行,同位角相等
2、现有两根木棒,它们的长度分别为
A、
3、如图 ,直线
,直线 分别交
分别交 、
、 于
于 、
、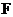 ,
, 的平分线交
的平分线交 于点
于点 ,若
,若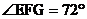 ,则
,则 等于(
)。
等于(
)。

A、36° B、54° C、72° D、108°
4、如图是象棋盘的一部分,若帅位于点 上,相位于点
上,相位于点 上,则炮位于( )点上。
上,则炮位于( )点上。

A、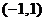 B、
B、 C、
C、 D、
D、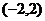
5、如图在直角三角形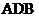 中,
中, ,
, 为
为 上一点,则
上一点,则 可能是(
)。
可能是(
)。
A、 B、
B、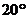 C、
C、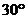 D、
D、

6、为迎接2008年奥运会的到来,某大型商城进行装修,准备用一种彩色砖对地面密铺,下列图形中仅能用同一种作平面镶嵌的是( )。
A、正三角形 B、正方形 C、正五边形 D、正六边形
7、如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需移动( )。

A、8格 B、9格 C、11格 D、l2格
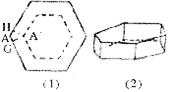
8、将一块正六边形硬纸片如图(1),做成一个底面仍为正六边形且高相等的无盖纸盒,侧面均垂直于底面,见图(2),需在每一个顶点处剪去一个四边形,例如图(1)中的四边形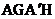 ,那么
,那么 的大小是(
)。
的大小是(
)。
A、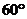 B、
B、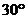 C、
C、 D、只要小于
D、只要小于 均可
均可
二、细心填一填,一锤定音。(本大题共8小题,每小题3分,共24分)
9、现实生活中有利用三角形稳定性的例子吗?请你写出来 。(至少写3个)
10、如图,直线 、CD
、CD 相交于O,且
相交于O,且 ,则
,则 的度数为 。
的度数为 。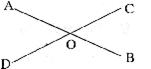
第10题图 第13题图
11、已知点 在第二象限,到
在第二象限,到 轴的距离是2,到
轴的距离是2,到 轴的距离是3,则点
轴的距离是3,则点 的坐标为 。
的坐标为 。
12、将命题“一个锐角的补角大于这个锐角的余角”改写成“如果……那么……”的形式为 。
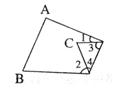
13、如上图,三角形纸片 中,
中, ,将纸片的一角折叠,使点
,将纸片的一角折叠,使点 落在
落在 内,若
内,若 ,则
,则 的度数为 。
的度数为 。
14、小明到工厂去进行社会实践活动,发现工人师傅生产了一种如图所示的零件,工人师傅告诉他: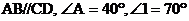 ,小明马上运用已学的数学知识得出了
,小明马上运用已学的数学知识得出了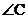 的度数,聪明的你一定知道
的度数,聪明的你一定知道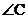 =
。
=
。
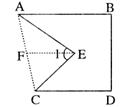
15、如图,图中利用有序实数对标出了部分方格的位置,请认真分析归纳,然后分别写出方格A、B、C、D,E,F对应的有序数对。
(3,3)
A
E
(4,3)
(1,1)
(2,1)
B
(0,0)
D
(1,2)
(2,2)
(3,4)
F
C
(4,4)
A: B: C:
D: E: F:
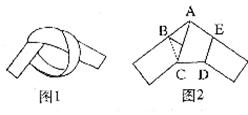
16、用一条宽相等的足够长的纸条,打一个结,如图l所示,然后轻轻拉紧、压平就可以得到如图2所示的正五边形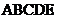 ,其中
,其中 = 度。
= 度。
三、用心解一解,马到成功。(本大题共8小题,总计72分)
17、(本题满分6分)
如图,修一条公路将村庄A、B与公路连结,该怎样修,才能使所修公路最短?画出线路图。你能根据作图,说出一个一般性的结论吗?

18、(本题满分6分)
已知 的三个顶点坐标如下表,将下表补充完整,并在直角坐标系中画出
的三个顶点坐标如下表,将下表补充完整,并在直角坐标系中画出 。
。
( )
)
(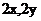 )
)
A(2, 1)
A′(4, 2)
B(4, 3)
B′( , )
C(5, 1)
C′( , )

19、(本题满分l0分)
已知一个多边形的内角和等于外角和的2倍,求这个多边形的边数及对角线的条数。
(1)已知:如图1, ,试说明
,试说明 ,过点
,过点 画
画 ,则
,则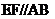 ,所以
,所以 ,
, ,所以
,所以 。
。
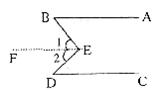
(2)如果上图中的E点位置发生变化,变为图2中的①、②、③,那么 、
、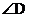 、
、
之间又有何关系?试说明理由。

21、(本题满分9分)
如图,按规定 、
、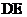 的延长线相交成
的延长线相交成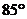 的角,因交点不在板上,不便测量,工人师傅连结
的角,因交点不在板上,不便测量,工人师傅连结 ,测得
,测得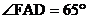 ,
, ,这时,
,这时, 、
、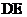 的延长线相交所成的角是不是符合规定?为什么?
的延长线相交所成的角是不是符合规定?为什么?

22、(本题满分l0分)
如图是某市旅游景点的示意图。科技大学、影月湖、大成殿、钟楼、中心广场、碑林、雁塔各景点分别都在格点上。

(1)若设一个方格的边长为一个单位,某人从影月湖去钟楼可选择怎样的方格线路最快到达目的地?若去碑林呢?
(2)若以科技大学为坐标原点,取向右和向上为数轴的正方向,一个方格的边长为一个单位,写出各个景点的坐标。
(3)想一想:建立怎样的直角坐标系,可以使大成殿和碑林在你选定的坐标系中的坐标分别为 和
和 ?
?
23、有趣玩一玩。(本题满分l0分)
中国象棋中的马颇有骑士风度,自古有“马踏八方”之说,如图(1),按中国象棋中“马”的行棋规则,图中的马下一步有A、B、C、D、E、F、G、H八种不同选择,它的走法就象一步从“日”字形长方形的对角线的一个端点到另一个端点,不能多也不能少。
要将图(2)中的马走到指定的位置P处,即从(四,6)走到(六,4),现提供一种走法:
(四,6)→(六,5)→(四,4)→(五,2)→(六,4)
(1)下面提供的另一走法,请你填上其中所缺的一步:
(四,6)→(五,8)→(七,7)→ →(六,4)
(2)请你再给出另一种走法(只要与前面的两种走法不完全相同即可,步数不限),你的走法是:

24、(本题满分l2分)
探索
在如图l至4中, 的面积为a。
的面积为a。
(1)如图l,延长 的边
的边 到点D,使
到点D,使 ,连结
,连结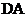 。若
。若 的面积为
的面积为 ,则
,则 =
(用含a的代数式表示);
=
(用含a的代数式表示);
(2)如图2,延长 的边
的边 点D,延长边
点D,延长边 到点E,使
到点E,使 ,连结
,连结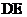 。若
。若 的面积为
的面积为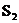 ,则
,则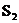 =
(用含a的代数式表示),并写出理由:
=
(用含a的代数式表示),并写出理由:
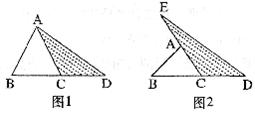
(3)在图2的基础上延长 到点F,使
到点F,使
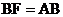 ,连结
,连结 、
、 ,得到
,得到 (如图3)。若阴影部分的面积为
(如图3)。若阴影部分的面积为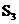 ,则
,则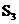 =
(用含
=
(用含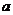 的代数式表示)。
的代数式表示)。
发现
像上面那样,将 各边均顺次延长一倍,连结所得端点,得到
各边均顺次延长一倍,连结所得端点,得到 (如图3),此时,我们称
(如图3),此时,我们称 向外扩展了一次。可以发现,扩展一次后得到的
向外扩展了一次。可以发现,扩展一次后得到的 的面积是原来
的面积是原来 面积的 倍。
面积的 倍。
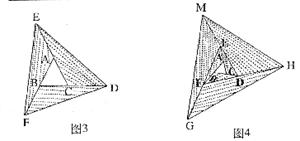
应用
去年在面积为 的
的 空地上栽种了某种花卉。今年准备扩大种植规模,把
空地上栽种了某种花卉。今年准备扩大种植规模,把 向外进行两次扩展,第一次由
向外进行两次扩展,第一次由 扩展成
扩展成 ,第二次由
,第二次由 扩展成
扩展成 (如图4)。求这两次扩展的区域(即阴影部分)面积共为多少
(如图4)。求这两次扩展的区域(即阴影部分)面积共为多少 ?
?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com