
2007年山东省莱芜市中等学校招生考试
数 学 试 题
注意事项:
1.答卷前,考生务必在试卷的规定位置将自己的姓名、准考证号等内容填写准确。
2.本试卷分第Ⅰ卷和第Ⅱ卷两部分。第Ⅰ卷为选择题,36分;第Ⅱ卷为非选择题,84分,满分120分。考试时间为120分钟。
3.请将第Ⅰ卷选择题的答案填写在第Ⅱ卷卷首答案栏内填写在其它位置不得分。
4.考试结束后,由监考老师把第Ⅰ卷和第Ⅱ卷一并收回。
第Ⅰ卷(选择题 共36分)
一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
1. 的绝对值是
的绝对值是
A.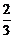 B.
B. C.
C. D.
D.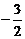
2.下列算式中,正确的是
A.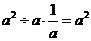
B.
C.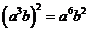
D.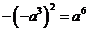
3.2007年4月,全国铁路进行了第六次大提速,提速后的线路时速达200千米,共改造约6000千米的提速线路,总投资约296亿元人民币,那么,平均每千米提速线路投资人民币的数额约是(用科学技术法,保留两个有效数字)
A. 亿元 B.
亿元 B.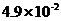 亿元
亿元
C. 亿元 D.
亿元 D. 亿元
亿元
4. 成立,则x的取值范围是
成立,则x的取值范围是
A. B.
B. C.
C.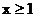 D.
D.
5.不等式2x-7<5-2x的正整数解有
A.1个 B.2个 C.3个 D.4个
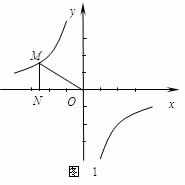
6.反比例函数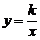 的图象如图1所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果
的图象如图1所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果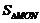 =2,则k的值为
=2,则k的值为
A.2 B.-
7.图2是韩老师早晨出门散步时,离家的距离(y)与时间(x)之间的函数图象.若用黑点表示韩老师家的位置,则韩老师散步行走的路线可能是



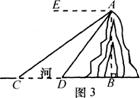
8.如图3,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,C、D、B在同一水平线上,又知河宽CD为
(A) +1)米 (D)
+1)米 (D)
9.如图4,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于

A.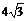 B.
B.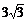 C.
C. D.8
D.8
10.对于任意的非零实数m,关于x的方程 根的情况是
根的情况是
A.有两个正实数根
B.有两个负实数根
C.有一个正实数根,一个负实数根
D.没有实数根
11.一个圆锥的高为3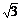 ,侧面展开图是半圆,则圆锥的侧面积是
,侧面展开图是半圆,则圆锥的侧面积是
A.9 B.
B. C.27
C.27 D.39
D.39
12.王英同学从A地沿北偏西60º方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地
A.150m B. m C.100 m D.
m C.100 m D. m
m
第Ⅱ卷(非选择题 共84分)
注意事项:
1.第Ⅱ卷共6页,用钢笔或圆珠笔直接写在试卷上.
2.答卷前将密封线内的项目填写清楚.
二、填空题:(每小题3分,共18分)
13.如果正数m的平方根为 和
和 ,则m的值是___________。
,则m的值是___________。
14.分解因式: .
.
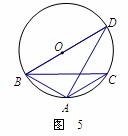
15.如图5,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则BC等于 .
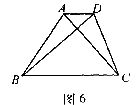
16.如图6,在梯形 中,
中,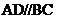 ,对角线
,对角线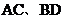 互相垂直,
互相垂直, ,中位线长为
,中位线长为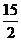 ,则对角线
,则对角线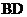 的长是______.
的长是______.
17.观察下列各式: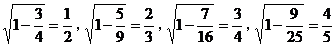 ,…,请你将猜想到的规律用含自然数n(n≥l)的代数式表示出来_____________________.
,…,请你将猜想到的规律用含自然数n(n≥l)的代数式表示出来_____________________.
18.线段AB,CD在平面直角坐标系中的位置如图7所示,O为坐标原点.若线段AB上一点P的坐标为(a,b),则直线OP与线段CD的交点的坐标为

三、解答题:本大题共7小题,共66分.解答要写出必要的文字说明、证明过程或演算步骤.
19. (本题满分8分)
解方程:
20. (本题满分9分)
数据段
频 数
频 率
30~40
10
0.05
40~50
36
50~60
0.39
60~70
70~80
20
0.10
总 计
1
将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数及频率如下表(未完成):
注:30~40为时速大于等于30千米而小于40千米,其它类同.
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果此地汽车时速不低于60千米即为违章,则违章车辆共有多少辆?

21.(本题满分9分)
已知:如图9,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

22. (本题满分9分)
在济青高速公路南线的施工过程中,某工程队承包了一段长18千米的道路修建工程,为了加快修建速度,工程负责人将工程队分为甲乙两组,从路的两端同时开工,两个组修建道路的长度与施工天数的关系如图10所示.

求:(1)开工多少天时,两个组修建道路的长度相同?
(2)此工程队完成任务共需要多少天?
23.(本题满分l0分)
如图11,△ABC是⊙O的内接三角形, ,D为⊙O中
,D为⊙O中 一点,延长DA至点E,使CE=CD.
一点,延长DA至点E,使CE=CD.
(1)求证: ;
;
(2)求证: ;
;
(3)若 ,求证:
,求证:  .
.

 24. (本题满分10分)
24. (本题满分10分)
已知:如图12,在△ABC中,D为AB边上一点, ,
,


(1)证明:△ADC和△BDC都是等腰三角形;
(2)若AB=1,求AC的值;
(3)试构造一个等腰梯形,该梯形连同它的两条对角线,得到了8个三角形,要求构造出的图形中有尽可能多的等腰三角形.(标明各角的度数)
25. (本题满分12分)
在平面直角坐标系中,△AOB的位置如图13所示,已知∠AOB=90º,AO=BO,点A的坐标为(-3,1).

(1)求点B的坐标;
(2)求过A,O,B三点的抛物线的解析式;
(3)设抛物线的对称轴为直线 ,P是直线
,P是直线 上的一点,且△PAB的面积等于△AOB.求点P的坐标。
上的一点,且△PAB的面积等于△AOB.求点P的坐标。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com