
2007-2008学年度济宁市嘉祥县第一学期期中考试
九年级数学试题
一、选择题(把正确答案写在答题栏中,每小题3分,共36分)
1.化简 的结果是
的结果是
A.10 B. C.4
C.4 D.20
D.20
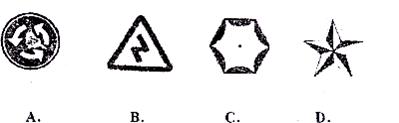
2.下列图形中既是轴对称图形又是中心对称图形的是
3.一元二次方程 的解是
的解是
A.
B.
C.
D.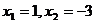
4.为执行“两免一补”政策,某地区2006年投入教育经费2500万元,预计2008年投入3600万元。设这两年投入教育经费的年平均增长百分率为 ,则下列方程正确的是
,则下列方程正确的是
A.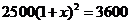 B.
B.
C.  D.
D.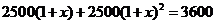
5.小明不慎把家里的圆形玻璃打碎了,其中四块碎片(如图所示),为配成与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是
A.第①块 B.第②块 C.第③块 D.第④块

6.如图,等边三角形ABC内接于圆O,动点P在圆周的劣弧AB上,且不与A、B重合,则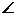 BPC等于
BPC等于
A.60º B.30º C.90º D.45º
7.如图,Rt ABC绕O点旋转90º得Rt
ABC绕O点旋转90º得Rt BDE,其中
BDE,其中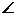 ACB=
ACB=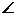 BED=90º,AC=3,DE=5,则OC的长为( )
BED=90º,AC=3,DE=5,则OC的长为( )
A. 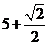 B.
B. 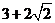 C.
C. D.
D.
8.已知 与
与 的半径长是方程
的半径长是方程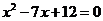 的两根,且
的两根,且
 =4,则
=4,则 与
与 的位置关系是
的位置关系是
A.相交 B.内切 C.内含 D.外切
9.边长分别为3、4、5的三角形的内切圆半径与外接圆半径之比为
A.1:5 B.4:5 C.3:5 D.2:5
10.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为
A.2cm B. cm C.2
cm C.2 cm D.2
cm D.2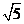 cm
cm

11.如图,在直角坐标系中, 的半径为1,则直线的位置关系是
的半径为1,则直线的位置关系是
A.相离 B.相交
C.相切 D.以上三种情形都有可能
12.已知半径为5的 中,弦AB=5
中,弦AB=5 ,弦AC=5,
,弦AC=5, BAC的度数是
BAC的度数是
A.15º B.210º C.210º或30º D.105º或l5º
二、填空题(每小题3分,共18分)
13.已知 是关于
是关于 的方程
的方程 的一个根,则
的一个根,则 = 。
= 。
14.如图,PA、PB切 于点A、B,点C是
于点A、B,点C是 上一点,
上一点,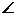 ACB=65º,则
ACB=65º,则 P= 。
P= 。


15.如图,两个圆的圆心都在 轴上,交点为A、B,已知点A的坐标为(
轴上,交点为A、B,已知点A的坐标为( 2,3),则点B的坐标为 。
2,3),则点B的坐标为 。
16.将4个数排成2行、2列,两边各加一条竖直线记成 ,定义
,定义 ,上述记号就叫做2阶行动式,若
,上述记号就叫做2阶行动式,若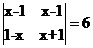 ,则x= 。
,则x= 。
17.为了测量一个圆形铁环的半径,某同学采用如下方法:将铁环平放在水平桌面上,用一个锐角为30º的三角板和一把刻度尺,按照如图所示的方法得到相关数据,进而可求得铁环的半径,若测得PA=5cm,则铁环的半径是 cm。

18.观察下列各式:
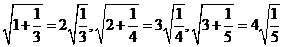 ……
……
请你将发现的规律用含自然数n(n≥1)的等式表示出来 。
三、解答题:
19. (8分)
(8分)
20.(8分)如图,方格纸中的每个小方格都是边长为l个单位的正方形,在建立平面直角坐标系后, ABC的顶点均在格点上,点C的坐标为(4,
ABC的顶点均在格点上,点C的坐标为(4, l)
l)
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1,并写出点C1的坐标;
(2)以原点O为对称中心,再画出与△A1B1C1关于原点O对称的△A2B2C2,并写出点C2的坐标;

21.(9分)某农场去年种植了l0亩地的南瓜,亩产量为2000kg,根据市场需要,今年该农场扩大了种植面积;并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率。
22.(9分)张宇同学是一名天文爱好者,他通过查阅资料得知:地球、火星的运行轨道可以近似地看成足以太阳为圆心的两个同心圆,且这两个同心圆在同一平面上(如图所示)。由于地球和火星的运行速度不同,所以二者的位置不断发生变化。 当地球、太阳和火星三者处在一条直线上,且太阳位于地球和火星中间时,称为“合”;当地球、太阳和火星三者处在一条直线上,且地球位于太阳与火星中间时,称为“冲”,另外,从地球上看火星与太阳,当两条视线互相垂直时,分别称为“东方照”和“西方照”,已知地球距太阳15(千万千米),火星距太阳20.5(千万千米)。
(1)分别求“合”、“冲”、“东方照”、“西方照”时,地球与火星的距离(结果保留准确值)。
(2)如果从地球上发射宇宙飞船登上火星,为了节省燃料,应选择在什么位置发射较好,说明你的理由。(注:从地球上看火星,火星在地球左、右两侧时分别做“东方照”、“西方照”)。

23.(10分)如图,AB是 的弦,矩形ABCD的边CD与
的弦,矩形ABCD的边CD与 交于点E、F,AF和BE相交于点G,连结AE、BF。
交于点E、F,AF和BE相交于点G,连结AE、BF。

(1)写出图中每一对全等的三角形(不再添加辅助线):
(2)选择你在(1)中写出的全等三角形中的任意一一对进行证明。
24.(10分)如图,在 中,AB是直径,
中,AB是直径,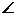 BOC=120º,PC是
BOC=120º,PC是 的切线,切点是C,点D在劣弧BC上运动。当
的切线,切点是C,点D在劣弧BC上运动。当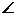 CPD满足什么条件时,直线PD与直线AB垂直?证明你的结论。
CPD满足什么条件时,直线PD与直线AB垂直?证明你的结论。

25.(12分)在△ABC中,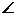 BAC=90º,AB=AC=2
BAC=90º,AB=AC=2 ,圆A半径为1,如图所示。若点O在BC边上运动(与点B,C不重合),设BO=
,圆A半径为1,如图所示。若点O在BC边上运动(与点B,C不重合),设BO= ,
, AOC的面积为
AOC的面积为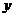 。
。

(1)求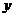 关于
关于 的函数解析式,并写出自变量
的函数解析式,并写出自变量 的取值范围。
的取值范围。
(2)以点O为圆心,BO长为半径作圆O,求当圆O与圆A相切时, AOC的面积。
AOC的面积。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com