
2007-2008学年度淄博市淄川第一学期期中考试
初二数学试题
亲爱的同学们:
这份试题将再次记录你的自信、沉着、智慧和收获,老师会一直投给你信任的目光。请你认真审题,看清要求,仔细答题。别忘了,还有5分的卷面分等你拿!祝你考出好成绩!为初二学年的期中数学学习画上圆满的句号!
一、精心选一选(本题县14小题,在每小题所给出的四个选项中,只有一个是正确的,请选出你认为唯一正确的答案,每小题3分,计42分)。
1.国旗是一个国家的象征。观察下面的国旗,其中是轴对称图形的有( )面

2.如下图,点D在△ABC的边BC上,且BC=BD+AD,则点D在线段( )的垂直平分线上
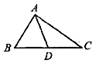
A.AB B.BC C.AC D.不能确定
3.在 (相邻两个l之间的0的个数逐次加2),
(相邻两个l之间的0的个数逐次加2), 中,无理数的个数是( )
中,无理数的个数是( )
A.5 B.
4.下列事件:(1)掷出一枚均匀的硬币,“国徽”面朝上(2)3人分成两组,一定有两人在一组(3)中国“飞人”刘翔1小时可以跑60千米(4)掷出一枚均匀的小正方体(每个面上分别标有l,2,3,4,5,6),朝上的数字小于6.上述事件发生的可能性标在图中 与
与 之间的有( )件
之间的有( )件

A.4 B.
5.如下图, 与
与 关于直线
关于直线 对称,则
对称,则 的度数为( )
的度数为( )

A.100
B.
6.观察下列数组:3,4,5;6,8,10;9,12,15;12,16.20;…21, , …。根据你观察并发现的规律,横线上应填的数字为( )
A.16,20 B.20,
7.下列说法正确的是( )
A.4的平方根是2 B.11没有平方根
C.(?25)2的平方根是±25 D.对于任意数 ,总有
,总有
8.现有四个袋子,标号分别为①②③④,每个袋子中所装的白球和黑球的个数如下表所示:如果闭着眼睛从袋子中任取一球,那么从哪个袋子最有可能摸到黑球?( )
①号袋
②号袋
③号袋
④号袋
黑球个数
20
12
12
20
白球个数
20
4
6
10
A.①号袋 B.②号袋 C.③号袋 D.④号袋
9.如下图,在△ABC中,∠A=90°,AB=AC,BD是∠ABC的平分线,DE⊥BC于E,若AB=a,AD=b,则△DEC的周长为( )
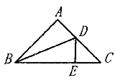
A.a B.b C.a+b D.以上都不对
10.若规定误差小于1,则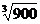 的估算值为( )
的估算值为( )
A.30 B.9或
11.小亮用一枚均匀的硬币做实验,前7次掷得的结果都是正面朝上,如果将第8次掷得正面朝上的概率记为P,则( )
A.p> B.p=
B.p= C.p<
C.p< D.无法确定
D.无法确定
12.有一个数值转换器,原理如下:

当输入的x为256时,输出的y是( )
A.2 B.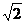
13.如下图,在Rt ABC中。分别以AB,AC,BC为直径作半圆,3个半圆的面积依次分别为S1,S2,S3。则S1,S2,S3的关系为( )
ABC中。分别以AB,AC,BC为直径作半圆,3个半圆的面积依次分别为S1,S2,S3。则S1,S2,S3的关系为( )
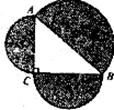
A.S1= S2+ S3 B.S1> S2+ S
14.小明从A点先向北行进
A.
二,细心填一填(本题共8小题,满分24分,只要求填写最后结果,每小题填对得3分)。
15.请你列举一个不确定事件: 。
16.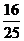 的平方根是 ;
的平方根是 ;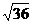 的算术平方根是 ;-0.125的立方根是 。
的算术平方根是 ;-0.125的立方根是 。
17.如图,将长方形ABCD沿AE折叠,若∠BAD′=26°,则∠AE D′ 度。
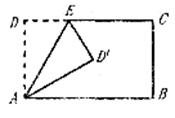
18。现有50张大小、质地及背面图案均相同的北京奥运会吉祥物福娃卡片,正面朝下放置在桌面上,从中随机抽取l张并记下卡片正面所绘福娃的名字后原样放回,洗匀后再抽,不断重复上述过程,最后记录抽到“欢欢”的频率为20%,则这些卡片中“欢欢”约为 张。
19.若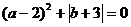 ,则
,则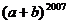 = 。
= 。
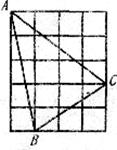
20.如图,正方形网格中,每个小正方形的边长为1,则网格上的三条边中,边长为无理数的有 条。
21.已知等腰三角形的一个内角为50°,则这个三角形腰上的高与底边的夹角是 度。
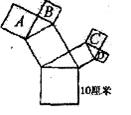
22.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为
三、耐心做一做,相信你能写出正确的解答过程(共54分,注意审题要细心,书写要规范和解答要完整)。
23.(本题满分9分)
如图,在 ABC中,D为BA延长线上的一点,AE平分∠CAD,且AE//BC,那么
ABC中,D为BA延长线上的一点,AE平分∠CAD,且AE//BC,那么 ABC一定为等腰三角形吗?为什么?
ABC一定为等腰三角形吗?为什么?

24.(本题满分7分)如图所示有九张卡片,每张卡片上分别标有如下的数字。将它们背面朝上洗匀后,任意抽出一张,分别计算下列事件发生的概率。

(1)P(抽到数字9)= ;
(2)P(抽到两位数)= ,P(抽到一位数)= ;
(3)P(抽到的数大于6)= ,P(抽到的数小于6)= ;
(4)P(抽到奇数)= ,P(抽到偶数)= 。
25.(本题满分12分)
(1) (2)
(2)
(3) (4)
(4)
(5)若 ,试求
,试求 的值。
的值。
26.正方形网格中的每个小正方形的边长都是1,任意连接这些小正方形的顶点,可得到一些线段。(1)请在图中画出线段 ,并选择其中的一条说明这样画的道理;(2)以
,并选择其中的一条说明这样画的道理;(2)以 为边组成的三角形是直角三角形吗?为什么?
为边组成的三角形是直角三角形吗?为什么?

27.(本题满分9分)
如图,AB=AC,DE是AB的垂直平分线,∠A=36°,CE=4, BCE的周长为24,求AB的长。
BCE的周长为24,求AB的长。
28.(本题满分7分)
(1)四年一度的国际数学家大会于
(2)现有一张长为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com