
2007临沂市中考模拟试题(四)
数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至8页,满分l20分。考试时间l20分钟。
第Ⅰ卷(选择题 共42分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试卷上。
3.考试结束,将本试卷和答题卡一并交回。
一、选择题(每小题3分,在给出的四个选项中,只有一项是符合题目要求的)
1.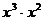 的运算结果是
的运算结果是
A.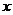 B.
B. C.
C.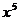 D.
D.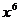
2.不等式组 的解集为
的解集为
A. B.
B. C.
C. D.
D.
3.已知不等边三角形的一边等于5,另一边等于3,若第三边长为奇数,则周长等于
A.13 8.
4.北京等5个城市的国际标准时间(单位:小时)可在数轴上表示如下,如果将两地国际标准时间的差简称为时差。那么

A.汉城与纽约的时差为13小时 B.汉城与多伦多的时差为13小时
C.北京与纽约的时差为14小时 D.北京与多伦多的时差为14小时
5.一只小狗正在平面镜前欣赏自己的全身像(如图)。此时,它所看到的全身像是

6.在函数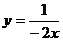 的图像上有三点
的图像上有三点 ,
, ,
, 。若
。若 ,则下列正确的是
,则下列正确的是
A. B.
B.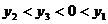
C. D.
D.
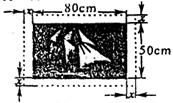
7.在一幅长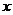 cm,那么
cm,那么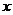 满足的方程是
满足的方程是
A. B
B
C.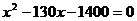 D.
D.
8.已知两圆的圆心距小于两圆的半径和,那么这两圆的位置关系为
A.相交 B.内切 C.内含 D.以上情况都有可能
9.下图可以看作是一个等腰直角三角形旋转若干次而生成的,则每次旋转的度数可以是

A.90º B.60º C.45º D.30º
10.用一把带有刻度尺的直角尺,①可以画出两条平行的直线 和
和 ,如图(1);②可以画出∠AOB的平分线OP,如图(2);③可以检验工件的凹面是否为半圆,如图(3);④可以量出一个圆的半径,如图(4)。这四种说法正确的有
,如图(1);②可以画出∠AOB的平分线OP,如图(2);③可以检验工件的凹面是否为半圆,如图(3);④可以量出一个圆的半径,如图(4)。这四种说法正确的有
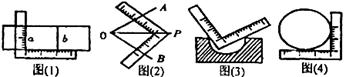
A.4个 B.3个 C.2个 D.1个
11.下列命题正确的个数是
①等腰三角形的腰长大于底边长;
②三条线段 、
、 、
、 ,如果
,如果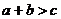 ,那么这三条线段一定可以组成三角形;
,那么这三条线段一定可以组成三角形;
③等腰三角形是轴对称图形。它的对称轴是底边上的高;
④面积相等的两个三角形全等。
A.0个 B.1个 C.2个 D.3个
12.在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度。则下图能反映弹簧称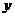 (单位N)与铁块被提起的高度
(单位N)与铁块被提起的高度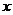 (单位cm)之间的函数关系的大致图象是
(单位cm)之间的函数关系的大致图象是

13.顺次连结四边形四条边的中点,所得的四边形是菱形,则原四边形一定是
A.平行四边形 B.对角线相等的四边形
C.矩形 D.对角线互相垂直的四边形
14.如图是测量一物体体积的过程:
步骤一:将180ml的水装进一个容量为300ml的杯子中。
步骤二:将三个相同的玻璃球放入水中,结果水没有满。
步骤三:同样的玻璃球再加一个放入水中,结果水满溢出。

根据以上过程,推测一颗玻璃球的体积在下列哪一范围内?(1ml=
A.
C.
15.法国的“小九九”从“一一得一”到“五五二十五”和我国的“小九九”是一样的,后面的就改用手势了。下面两个图框使用法国“小九九”计算7×8和8×9的两个示例。若用法国的“小九九”计算7×9,左、右手依次伸出手指的个数是
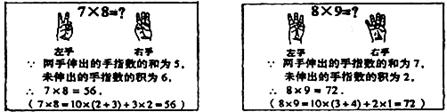
A.2,3 B.3,
第Ⅱ卷 非选择题(78分)
二,填空题(本大总共5小题,每小题3分,共l5分.将答案填写在对应题号的横线上。)
15.一射击运动员在一次射击练习中打出的成绩是(单位:环):7,8,9,8,6,8,10,7,这组数据的众数是 环。
16.如图,∠ACB∠ADB。要使△ACB≌△BDA,请写出一个符合要求的条件 。

17.如图所示,在边长为 的正方形中剪去一个边长为
的正方形中剪去一个边长为 的小正方形(
的小正方形( ),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分的面积,验证了公式
。
),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分的面积,验证了公式
。
18.如图的围棋盘放在某个平面直角坐标系内,白棋②的坐标为(-8, -5),白棋④的坐标为(-7, -9),那么黑棋①的坐标应该是 。
19.如图,在世界杯足球比赛中.甲带球向对方球门PQ进攻,当他带球冲到A点时,同伴乙已经助攻冲到B点。有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门,仅从射门角度考虑,应选择 种射门方式。

20.右上图是一回形图,其圆形通道的宽和OB的长均为1,回形线与射线OA交于Al,A2,A3,…。若从O点到A1点的圆形线为第1圈(长为7)。从点A1到点A2的回形线为第2圈,…依此类推。则第10圈的长为 。
三、解答题:
20.计算(满分6分)
计算: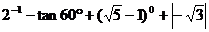
21.(本题满分8分)
如图所示,秋千链子的长度为
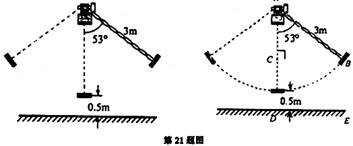
22.(本题满分7分)
如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P。
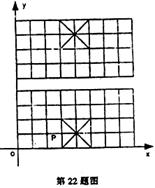
(1)写出下一步“马”可能到达的点的坐标 ;
(2)顺次连接(1)中的所有点,得到的图形是 图形(填“中心对称”、“旋转对称”、“轴对称”);
(3)指出(1)中关于点P成中心对称的点 。
23.(本题满分6分)
如图,一条毛毛虫要从A处去吃树叶,毛毛虫在交叉路口B、C、D、E处选择任何树杈都是可能的。求下列概率:
(1)吃到树叶l的概率;
(2)吃到树叶的概率;

24.(本题满分8分)
为了配合“八荣八耻”宣传教育,针对闯红灯的现象时有发生的实际情况,八年级某班开展一次题为“红灯与绿灯”的课题学习活动,它们将全班学生分成8个小组,其中第①~⑥组分别负责早、中、晚三个时段闯红灯违章现象的调查,第⑦小组负责查阅有关红绿灯的交通法规,第⑧小组负责收集有关的交通标志。数据汇总如下:
部分时段车流量情况调查表
时间
负责组别
车流总量
每分钟车流量
早晨上学6:30―7:00
①②
2747
92
中午放学11:20―11:50
③④
1449
48
下午放学5:00―5:30
⑤⑥
3669
122

回答下列问题:
(1)请你写出2条交通法规:① ,② 。
(2)画出2枚交通标志并说明标志的含义。

(3)早晨、中午、晚上三个时段每分钟车流量的极差是 ,这三个时段的车流总量的中位数是 。
(4)观察表中的数据及条形统计图,写出你发现的一个现象并分析其产生的原因。
(5)通过分析写一条合理化建议。
25.(本题满分8分)
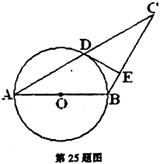
已知:如图,AB是⊙O的直径,⊙O过AC的中点D,DE切⊙O于点D,交BC于点E。
(1)求证:DE⊥BC;
(2)如果CD=4,CE=3.求⊙O的半径。
26.(本题满分l0分)
某公司试销一种成本为30元/件的新产品,按规定试销时的销售单价不低于成本单价,又不高于80元/件。试销中每天的销售量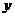 (件)与销售单价
(件)与销售单价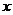 (元/件)满足下表中的函数关系。
(元/件)满足下表中的函数关系。
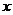 (元/件)
(元/件)
35
40t
45
50
55
y(件)
550
500
450
400
350
(1)试求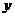 与
与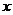 之间的函数表达式;
之间的函数表达式;
(2)设公司试销该产品每天获得的毛利润为S(元),求S与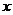 之间的函数表达式(毛利润=销售总价-成本总价);
之间的函数表达式(毛利润=销售总价-成本总价);
(3)当销售单价定为多少时,该公司试销这种产品每天获得的毛利润最大?最大毛利润是多少?此时每天的销售量是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com