
2007年镇江市初中毕业、升学统一考试
数 学
本试卷共3大题,28题,满分120分,考试时间120分钟.闭卷考试。
希望你沉着冷静,相信你一定能成功!
一、填空题(本大题共9小题,每小题2分,共18分.请将答案填在题中横线上)
1.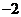 的相反数是
,
的相反数是
,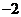 的绝对值是 .
的绝对值是 .
2.计算: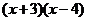 =_____________,分解因式:
=_____________,分解因式: =_______ .
=_______ .
3.若代数式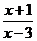 的值为零,则x=________;若代数式
的值为零,则x=________;若代数式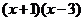 的值为零,则x=_______。
的值为零,则x=_______。
4.如图(1),∠ABC=∠DBC,请补充一个条件:_________________,使△ABC≌△DBC。
如图(2),∠1=∠2,请补充一个条件:__________________,使△ABC∽△ADE。
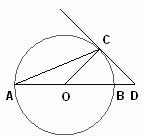
5. 如图,AB是⊙O的直径,C是⊙O上一点,过点C的切线交AB的延长线于点D。若∠BAC=25°,则∠COD的度数为_______,∠D的度数为________。
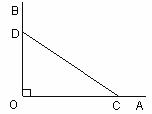
6.如图,矩形ABCD的对角线相交于O,AB=2,∠AOB=60°,则对角线AC的长为 .

7.按下图中的程序运算:当输入的数据为4时,则输出的数据是________。

8.如图,菱形ABCD的对角线相交于O,AC=8,BD=6,则边AB的长为_______。

9.在一张三角形纸片中,剪去其中一个50°的角,得到如图所示的四边形,则图中∠1+∠2的度数为______________。

二、选择题:本大题共9小题,每小题3分,共27分。每小题都给出代号为A、B、C、D的四个结论,其中有且只有一个结论是正确的,请将正确结论的代号填在题后的括号内。
10.下列运算正确的是( )
A.  B.
B.
C. D.
D.
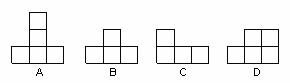
11.由若干个小立方块所搭成的几何体的主视图、左视图如下图所示,则该几何体的俯视图不可能是( )

12.为了了解某小区居民的用水情况,随机抽查了该小区10户家庭的月用水量,结果如下:
月用水量(t)
10
13
14
17
18
户 数
2
2
3
2
1
则这10户家庭月用水量的众数和中位数分别为( )
A.14t,13.5t B.14t,13t C.14t,14t D.14t,10.5t
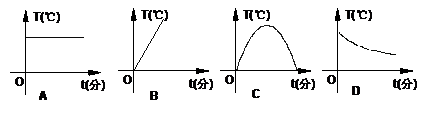
13.一杯水越晾越凉,则可以表示这杯水的水温T(℃)与时间t(分)的函数关系的图像大致是( )
14.如图,AB是⊙O的弦,OC⊥AB,垂足为C,若⊙O的半径为5,OC=3,则弦AB的长为( )

A.4 B.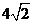
15.如图,在△ABC中,∠BAC=90°,AB=AC,O为△ABC内一点,AO=2,如果把△ABO绕点A按逆时针方向旋转90°,使AB与AC重合,则点O运动的路径长为( )
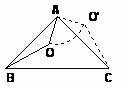
A.2 B.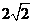 C.
C. D.π
D.π
16.一个机器人从数轴原点出发,沿数轴正方向。以每前进3步后退2步的程序运动。设该机器人每秒钟前进或后退1步,并且每步的距离是1个单位长,xn表示第n秒时机器人在数轴上的位置所对应的数。给出下列结论:⑴ ;⑵
;⑵ ;⑶
;⑶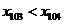 ;⑷
;⑷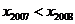 。
。
其中,正确结论的序号是( )
A.⑴、⑶ B.⑵、⑶ C.⑴、⑵、⑶ D.⑴、⑵、⑷
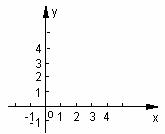
17.已知对应关系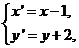 ,其中,(x,y)、(x’,y’)分别表示△ABC、△A’B’C’的顶点坐标。若△ABC在直角坐标系中的位置如图所示,则△A’B’C’的面积为( )
,其中,(x,y)、(x’,y’)分别表示△ABC、△A’B’C’的顶点坐标。若△ABC在直角坐标系中的位置如图所示,则△A’B’C’的面积为( )
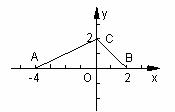
A.3 B.6 C.9 D.12
18.在直角坐标系中有两条直线l1、l2,直线l1所对应的函数关系式为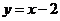 ,如果将坐标纸折叠,使l1与l2重合,此时点(-1,0)与点(0,-1)也重合,则直线l2所对应的函数关系式为(
)
,如果将坐标纸折叠,使l1与l2重合,此时点(-1,0)与点(0,-1)也重合,则直线l2所对应的函数关系式为(
)
A.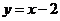 B.
B.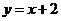 C.
C. D.
D.
三、解答题(本大题共10小题,共75分.解答应写出文字说明、证明过程或推演步骤)
19.(本小题满分10分)计算或化简:
(1) ;
(2)
;
(2) .
.
20.(本小题满分10分)解方程或解不等式组:
(1) ;
(2)
;
(2)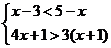
21.(本小题满分6分)
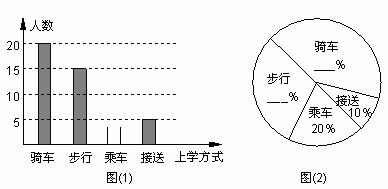
学生的上学方式是初中生生活自理能力的一种反映。为此,某校教导处组织部分初三学生,运用他们所学的统计知识,对初一学生上学的四种方式:骑车、步行、乘车、接送,进行抽样调查,并将调查的结果绘制成图(1)、图(2)。
请根据图中提供的信息,解答下列问题:
(1) 抽样调查的样本容量为________,其中步行人数占样本容量的_____%,骑车人数占样本容量的______%。
(2) 请将图(1)补完整。
(3) 根据抽样调查结果,你估计该校初一年级800名学生中,大约有多少名学生是由家长接送上学的?
(4) 你有什么话想对由家长接送上学的同学说?(一般不超过20个字)
22.(本小题满分6分)
已知,如图,在 中,E、F分别是AD、BC的中点.
中,E、F分别是AD、BC的中点.
求证:⑴ △ABE≌△CDF.
⑵ BE=DF.
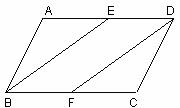
23.(本小题满分6分)

如图,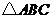 是⊙O的内接三角形,D是
是⊙O的内接三角形,D是 的中点,BD交AC于点E.
的中点,BD交AC于点E.
(1)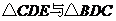 相似吗?为什么?;
相似吗?为什么?;
(2)若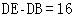 ,求DC的长.
,求DC的长.
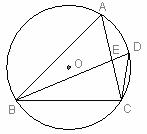
24.(本小题满分6分)
已知抛物线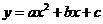 的对称轴是经过点(2,0)且与y轴平行的直线,抛物线与x轴相交于点A(1,0),与y轴相交于点B(0,3),其在对称轴左侧的图像如图所示。
的对称轴是经过点(2,0)且与y轴平行的直线,抛物线与x轴相交于点A(1,0),与y轴相交于点B(0,3),其在对称轴左侧的图像如图所示。
⑴ 求抛物线所对应的函数关系式,并写出抛物线的顶点坐标。
⑵ 画出抛物线在对称轴右侧的图像,并根据图像,写出当x为何值时,y<0。
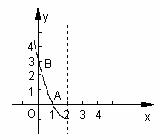
25.(本小题满分6分)
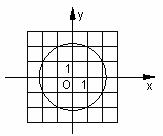
如图,⊙O的半径是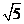 ,圆心与坐标原点重合,在直角坐标系中,把横坐标、纵坐标都是整数的点称为格点。
,圆心与坐标原点重合,在直角坐标系中,把横坐标、纵坐标都是整数的点称为格点。
⑴ 写出⊙O上所有格点的坐标:
___________________________________________________。
⑵
设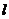 为经过⊙O上任意两个格点的直线。
为经过⊙O上任意两个格点的直线。
① 满足条件的直线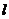 共有多少条?
共有多少条?
② 求直线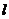 同时经过第一、二、四象限的概率。
同时经过第一、二、四象限的概率。
26.(本小题满分7分)
画图、证明:如图, ,点C、D分别在OA、OB上。
,点C、D分别在OA、OB上。
⑴ 尺规作图(不写作法,保留作图痕迹):作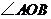 的平分线OP;作线段CD的垂直平分线EF,分别与CD、OP相交于E、F;连结OE、CF、DF。
的平分线OP;作线段CD的垂直平分线EF,分别与CD、OP相交于E、F;连结OE、CF、DF。
⑵ 在所画图中,
① 线段OE与CD之间有怎样的数量关系:_____________。
② 求证:△CDF为等腰直角三角形。
27.(本小题满分8分)
探索、研究:仪器箱按如图方式堆放(自下而上依次为第1层、第2层、……),受堆放条件限制,堆放时应符合下列条件:每层堆放仪器箱的个数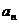 与层数
与层数 之间满足关系式
之间满足关系式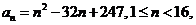
 为整数。
为整数。
⑴ 例如,当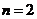 时,
时,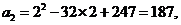 则
则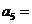 _____,
_____,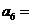 _____。
_____。
⑵ 第n层比第(n+1)层多堆放多少个仪器箱?(用含n的代数式表示)。
⑶ 如果不考虑仪器箱堆放所承受的压力,请根据题设条件判断仪器箱最多可以堆放几层?并说明理由。
⑷ 设每个仪器箱重54N(牛顿),每个仪器箱能承受的最大压力为160N,并且堆放时每个仪器箱承受的压力是均匀的。
① 若仪器箱仅堆放第1、2两层,求第1层中每个仪器箱承受的平均压力。
② 在确保仪器箱不被损坏的情况下,仪器箱最多可以堆放几层?为什么?
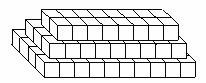
28.(本小题满分10分)
探索、研究:下图是按照一定的规律画出的一列“树型”图,下表的n表示“树型”图的序号,an表示第n个“树型”图中“树枝”的个数。
图:
n
1
2
3
4
…
an
1
3
7
15
…
表:
⑴ 根据“图”、“表”可以归纳出an关于n的关系式为____________________。
若直线 经过点
经过点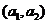 、
、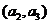 ,求直线
,求直线 对应的函数关系式,并说明对任意的正整数n,点
对应的函数关系式,并说明对任意的正整数n,点 都在直线
都在直线 上。
上。
⑵ 设直线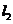 :
: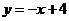 与x轴相交于点A,与直线
与x轴相交于点A,与直线 相交于点M,双曲线
相交于点M,双曲线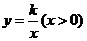 经过点M,且与直线
经过点M,且与直线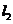 相交于另一点N。
相交于另一点N。
① 求点N的坐标,并在如图所示的直角坐标系中画出双曲线及直线 、
、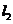 。
。
② 设H为双曲线在点M、N之间的部分(不包括点M、N),P为H上一个动点,点P的横坐标为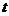 ,直线MP与x轴相交于点Q,当
,直线MP与x轴相交于点Q,当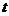 为何值时,
为何值时,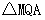 的面积等于
的面积等于 的面积的2倍?又是否存在
的面积的2倍?又是否存在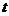 的值,使得
的值,使得 的面积等于1?若存在,求出
的面积等于1?若存在,求出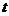 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
③ 在y轴上是否存在点G,使得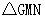 的周长最小?若存在,求出点G的坐标;若不存在,请说明理由。
的周长最小?若存在,求出点G的坐标;若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com