
2007-2008学年度德州市陵县第一学期期末考试
九年级数学试题
一、选择题(每题A、B、C、D四个选项中只有一个是最符合要求的,每小题3分,共24分)
1.已知关于 的方程
的方程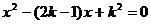 有两个不相等的实数根,那么k的最大整数值是( )
有两个不相等的实数根,那么k的最大整数值是( )
A.一2 B.一l C.0 D.1
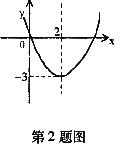
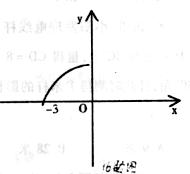
2.小明从图示的二次函数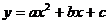 的图象中,观察得出以下五条信息①a<0 ②c=0 ③函数的最小值为一3 ④当
的图象中,观察得出以下五条信息①a<0 ②c=0 ③函数的最小值为一3 ④当 <0时,y>0。⑤当0<
<0时,y>0。⑤当0< <2时,
<2时,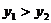 你认为其中正确的个数是( )
你认为其中正确的个数是( )
A.2 B.
3.把抛物线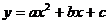 的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为
的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为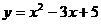 ,则有( )
,则有( )
A.b=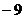 c=
c=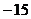 C.b=
C.b=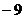 c=21
c=21
4.一袋子中有4颗球,分别标记号码1,2,3,4,已知每颗球被取出的机会相同,若第一次从袋中取出一颗球后放回,第二次从袋中再取出一球,则第二次取出球的号码比第一次大的几率为( )
A. B.
B.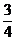 C.
C.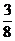 D.
D.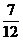
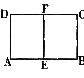
5.如图,一张矩形报纸ABCD的长AB=acm,宽BC=bcm,E、F分别是AB、CD的中点,将这张报纸沿着直线EF折叠后,矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比,则a:b等于( )
A.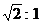 B.1:
B.1: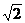 C.
C.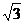 :1 D.1:
:1 D.1: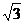
6.如图,△ABC与△DEF是位似图形,相似比为2:3,已知AB=4,则DE的长等于( )
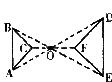
A.6 B.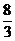
7.每年的正月十五,德州市都要举办放礼花的活动,今年预计一种新型的礼炮,这种礼炮的升空高度h(m)与飞行的时间t(s)的关系式是: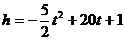 若这种礼炮在点火升空到最高点引爆,则从点火升空到引爆需要的时间是( )
若这种礼炮在点火升空到最高点引爆,则从点火升空到引爆需要的时间是( )
A.3s B.4s C.5s D.6s
8.如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=

A.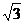 )米 D.(14+2
)米 D.(14+2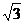 )米
)米
二、填空(每题3分,共24分)
9.如图所示的抛物线是二次函数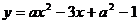 的图象,那么a的值是 。
的图象,那么a的值是 。

10.如图,在Rt△ABC中,∠C=90°,AC=BC=a,分别以A、B、C为圆心,以 AC为半径画弧,三条弧与边AB所围成的阴影部分面积为
。
AC为半径画弧,三条弧与边AB所围成的阴影部分面积为
。

11.已知二次函数 的部分图象如图所示,则关于
的部分图象如图所示,则关于 的一元二次方程
的一元二次方程 的解为
。
的解为
。

12.已知⊙O的半径等于
13.如图将一块斜边为

14.在一张比例尺为l:50000的地图上,一个多边形地块的周长为
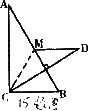
15.如图,Rt△ABC中,∠ACB=90°,∠A<∠B,以AB边上的中线CM为折痕将△ACM折叠,使点A落在点D处,如果CD恰好与AB垂直,则tanA=
16.抛物线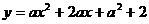 的一部分如图所示,那么该抛物线在y轴右侧与
的一部分如图所示,那么该抛物线在y轴右侧与 轴交点坐标是
轴交点坐标是
三、解答题(17、18每题6分,19、20每题8分,21、22每题10分,23、24每题12分,共72分)
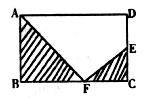
17.将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边F点处,已知CE=
18.关于 的一元二次方程
的一元二次方程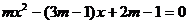 ,其根的判别式的值为1,求 m的值及该方程的根
,其根的判别式的值为1,求 m的值及该方程的根
19.在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的转盘,(如图所示,转盘被平均分成16份)并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会;如果转盘停止后,指针正好对准红色,黄色,绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物。如果顾客不愿意转转盘,那么可以直接得购物券10元

(1)求每转动一次转盘所获得的购物券金额的平均数
(2)如果你在商场消费125元,你会选择转转盘还是直接获得购物券,试说明理由
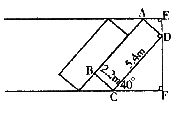
20.如图,ABCD是供一辆机动车停放的车位示意图,请你参考图中数据,计算车位所占街道的宽度EF(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84.结果精确到0.
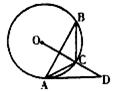
21.如图,△ABC内接于⊙O,点D在OC的延长线上,sinB= ,∠CAD=30°
,∠CAD=30°
(1)求证:AD是⊙O的切线
(2)若OD⊥AB,BC=5,求AD的长
22.等腰直角三角形ABC的面积为
23.如图,对称轴为直线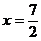 的抛物线过点A(0,6)和B(0,4)
的抛物线过点A(0,6)和B(0,4)
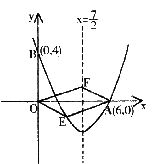
(I)求抛物线的解析式及顶点坐标
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求平行四边形OEAF的面积S与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围:
的取值范围:
①当S平行四边形OEAF=24时,请判断平行四边形OEAF是否为菱形。
②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标,若不存在,请说明理由。
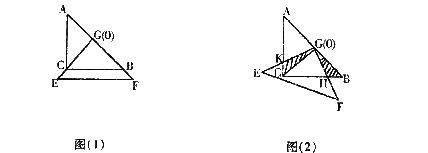
24.把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起(如图①所示),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,现将三角板EFO绕O点按顺时针方向旋转(旋转角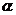 满足条件:0°<
满足条件:0°<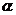 <90°)四边形CHGK是旋转过程中两三角板的重叠部分(如图②所示)
<90°)四边形CHGK是旋转过程中两三角板的重叠部分(如图②所示)
(1)在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论。
(2)连接HK,在上述旋转过程中,设BH= ,△GKH的面积为y,求y与
,△GKH的面积为y,求y与 的函数关系式,并写出
的函数关系式,并写出 的取值范围。
的取值范围。
(3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的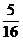 ?若存在,求出此时
?若存在,求出此时 的值,若不存在,说明理由。
的值,若不存在,说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com