
2007年安徽省初中毕业学业考试
数学试卷
考生注意:本卷共八大题,计23小题,满分 150 分,考试时间 120 分钟。
一、选择题(本题共10 小题,每小题4 分,满分40分)
1. 相反数是
( )
相反数是
( )
A. B.
B. C.
C. D.
D. 
2.化简(-a2)3的结果是 ( )
A.-a5
B. a
3.今年“五一”黄金周,我省实现社会消费的零售总额约为94亿元。若用科学记数法表示,则94亿可写为 ( )
A.0.94×109
B. 9.4×
4.下列调查工作需采用的普查方式的是 ( )
A.环保部门对淮河某段水域的水污染情况的调查
B.电视台对正在播出的某电视节目收视率的调查
C.质检部门对各厂家生产的电池使用寿命的调查
D.企业在给职工做工作服前进行的尺寸大小的调查
5.下列图形中,既是中心对称又是轴对称的图形是 ( )

6.化简 的结果是
( )
的结果是
( )
A.-x-1 B.-x+ D.
D. 
7.如图,已知AB∥CD,AD与BC相交于点P,AB=4,CD=7,AD=10,则AP的长等于( )

A.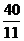 B.
B.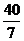 C.
C.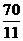 D.
D. 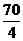
8.挂钟分针的长
A.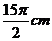 B.
B.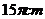 C.
C.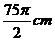 D.
D. 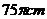
9.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示,设小矩形的长和宽分别为x、y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是 ( )

10.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ= ( )
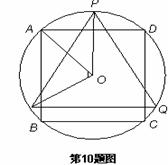
A.60° B. 65° C. 72° D. 75°
二、填空题(本题共 4 小题,每小题 5 分,满分 20 分)
11.5-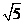 的整数部分是_________
的整数部分是_________
12.如图,已知∠1=100°,∠2=140°,那么∠3=______

13.两个小组进行定点投篮对抗赛,每组6名组员,每人投10次。两组组员进球数的统计如下:
组别
6名组员的进球数
平均数
甲组
8
5
3
1
1
0
3
乙组
5
4
3
3
2
1
3
则组员投篮水平较整齐的小组是____________________组。
14.如图是由四个相同的小立方体组成的立体图形的主视图和左视图,那么原立体图形可能是___________________。(把下图中正确的立体图形的序号都填在横线上)。

三.(本题共 2 小题,每小题 8 分,满分 16 分)
15.解不等式3x+2>2 (x-1),并将解集在数轴上表示出来。

16.△ABC和点S在平面直角坐标系中的位置如图所示:
⑴将△ABC向右平移4个单位得到△A1B
⑵将△ABC绕点S按顺时针方向旋转90°,画出旋转后的图形。

四、(本题共2小题,每小题8分,满分16分)
17.在“妙手推推推”的游戏中,主持人出示了一个9位数 ,让参加者猜商品价格。被猜的价格是一个4位数,也就是这个9位中从左到右连在一起的某4个数字。如果参与者不知道商品的价格,从这些连在一起的所有4位数中,任意猜一个,求他猜中该商品价格的概率。
,让参加者猜商品价格。被猜的价格是一个4位数,也就是这个9位中从左到右连在一起的某4个数字。如果参与者不知道商品的价格,从这些连在一起的所有4位数中,任意猜一个,求他猜中该商品价格的概率。
18.据报道,我省农作物秸杆的资源巨大,但合理利用量十分有限,2006年的利用率只有30%,大部分秸杆被直接焚烧了,假定我省每年产出的农作物秸杆总量不变,且合理利用量的增长率相同,要使2008年的利用率提高到60%,求每年的增长率。(取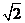 ≈1.41)
≈1.41)
五、(本题共2小题,每小题10分,满分20分)
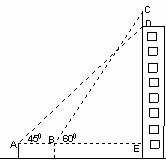
19.如图,某幢大楼顶部有一块广告牌CD,甲乙两人分别在相距 ≈1.73,计算结果保留整数)
≈1.73,计算结果保留整数)
20.如图,DE分别是△ABC的边BC和AB上的点,△ABD与△ACD的周长相等,△CAE与△CBE的周长相等。设BC=a,AC=b,AB=c。
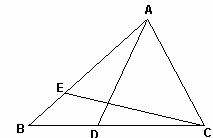
⑴求AE和BD的长;
⑵若∠BAC=90°,△ABC的面积为S,求证:S=AE?BD
六、(本题满分 12 分)
21.探索n×n的正方形钉子板上(n是钉子板每边上的钉子数),连接任意两个钉子所得到的不同长度值的线段种数:
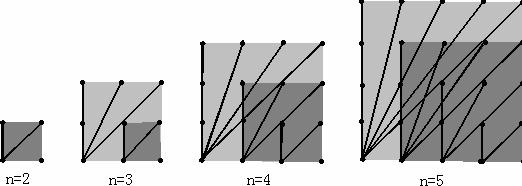
当n=2时,钉子板上所连不同线段的长度值只有1与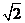 ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1,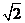 ,2,
,2,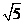 ,2
,2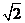 五种,比n=2时增加了3种,即S=2+3=5。
五种,比n=2时增加了3种,即S=2+3=5。
(1) 观察图形,填写下表:
钉子数(n×n)
S值
2×2
2
3×3
2+3
4×4
2+3+( )
5×5
( )
(2) 写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可)
(3)对n×n的钉子板,写出用n表示S的代数式。
七、(本题满分 12 分)
22..如图1,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点P是对角线BD上的一点,PQ∥BA交AD于点Q,PS∥BC交DC于点S,四边形PQRS是平行四边形。
(1)当点P与点B重合时,图1变为图2,若∠ABD=90°,求证:△ABR≌△CRD;
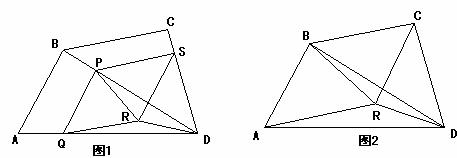
(2)对于图1,若四边形PRDS也是平行四边形,此时,你能推出四边形ABCD还应满足什么条件?
八、(本题满分 14 分)
23.按右图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
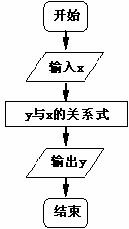
(Ⅰ)新数据都在60~100(含60和100)之间;
(Ⅱ)新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大。
(1)若y与x的关系是y=x+p(100-x),请说明:当p=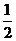 时,这种变换满足上述两个要求;
时,这种变换满足上述两个要求;
(2)若按关系式y=a(x-h)2+k (a>0)将数据进行变换,请写出一个满足上述要求的这种关系式。(不要求对关系式符合题意作说明,但要写出关系式得出的主要过程)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com