
2007-2008学年度聊城市阳谷县第一学期期末学业水平检测与反馈
九年级数学试题
一、选择题(每小题3分,共30分)
1. 的绝对值等于(
)
的绝对值等于(
)
A. B.
B.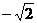 C.
C. D.
D.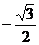
2.已知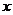 =1是一元二次方程
=1是一元二次方程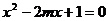 的一个解,则m的值是( )
的一个解,则m的值是( )
A.1 B.
3.A、B两地实际距离是
A.1:10 B.1:
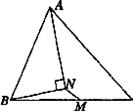
4.如图所示,在△ABC中,M为BC的中点,AN平分∠BAC,BN⊥AN,若AB=14,AC=19,则MN的长为( )
A.2 B.
5.△ABC中,∠A、∠B均为锐角,且有 ,则△ABC是 ( )
,则△ABC是 ( )
A.直角(不等腰)三角形 B.等腰直角三角形
C.等腰(不等边)三角形 D.等边三角形
6.在一个暗箱里放入除颜色外其它都相同的3个红球和11个黄球搅拌均匀后随机任取一个球,取到红球的概率是( )
A.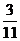 B.
B.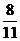 C.
C. D.
D.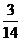
7.某市在旧城改造中计划在一块如图所示的三角形空地上种植某种草皮以美化环境,已知这种草皮每平方米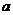 元,则购买这种草皮至少要( )
元,则购买这种草皮至少要( )

A.450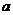 元
B.225
元
B.225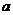 元
C.150
元
C.150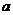 元 D.300
元 D.300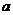 元
元
8.已知直线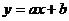 和抛物线
和抛物线 在同一坐标系中的大致图象正确的是 ( )
在同一坐标系中的大致图象正确的是 ( )

9.将抛物线 向左平移2个单位,再向下平移3个单位,所得的抛物线是( )
向左平移2个单位,再向下平移3个单位,所得的抛物线是( )
A.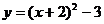 B.
B.
C. D.
D.
10.已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后点D落在CB的延长线上的D’处,那么tan∠BAD’等于( )

A.1 B. C.
C. D.
D.
二、填空题(每小题3分,共30分)
1.把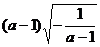 根号外面的因式移到根号内,结果为
根号外面的因式移到根号内,结果为
2.已知2<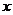 <5,化简
<5,化简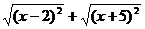 =
=
3.对于一元二次方程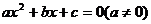 ,当
,当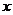 =1时,
=1时,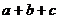 =
=
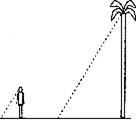
4.在同一时刻,小明测得他的影长为
5.将点A(3,1)绕原点O按顺时针方向旋转90°到点B,则点B的坐标是
6.已知△ABC∽△A1B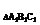 之比为
之比为
7.已知sin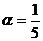 ,
,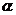 为锐角,则cos
为锐角,则cos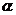 =
=
8.小华与父母一同乘火车从阳谷到聊城孔繁森纪念馆参观,火车车厢里每排有左、中、右三个座位,小华一家三口随意坐某排的三个座位,则小华恰好在中间的概率是 .
9.已知二次函数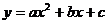 的图象如下图所示,则这个二次函数的关系式为:
的图象如下图所示,则这个二次函数的关系式为:
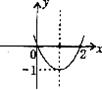
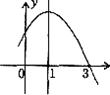
10.已知二次函数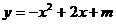 的部分图象如图所示,则关于
的部分图象如图所示,则关于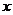 的一元二次方程
的一元二次方程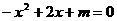 的解为
的解为
三、计算题(每小题8分,共24分)
1.解方程: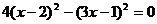
2.sin230°+cos230°+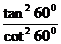
3.已知: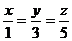 ,求:
,求: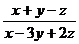
四、解答下列各题(共66分)
1.(10分)某农户种植花生,原种植的花生亩产量为200千克,出油率为50%(即每100千克花生可加工成花生油50千克),现在种植新品种花生后,每亩收获的花生可加工成花生油132千克,其中花生出油率的增长率是亩产量增长率的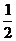 ,求新品种花生亩产量的增长率.
,求新品种花生亩产量的增长率.
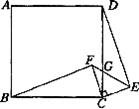
2.(11分)如图所示,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.
(1)求证:△BCF≌△DCE
(2)若BC=5,CF=3,∠BFC=90°,求:DG:GC的值.
3.(12分)北京2008奥运会吉祥物是“贝贝,晶晶、欢欢、迎迎、妮妮”,现将三张分别印有“欢欢、迎迎、妮妮”这三个吉祥物图案的卡片(卡片的形状大小一样,质地相同)放入盒子里.
(1)小玲从盒子中任取一张,取到印有“欢欢”图案的卡片的概率是多少?
(2)小玲从盒子中任取一张卡片,记下名字后放回,再从盒子中任取第二张卡片,记下名字,用列表或画树状图,列出小玲取到的卡片的所有可能情况,并求出小玲两次都取到印有“欢欢”图案的卡片的概率.
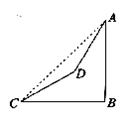
4.(10分)已知:如图,在山脚的C处测得山顶A的仰角为45°,沿着坡度为30°的斜坡前进
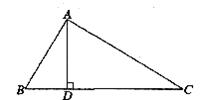
5.(10分)如图已知AD是△ABC边BC上的高,且AD2=BD?DC.
求证:∠BAC=90°.
6.(13分)已知二次函数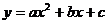 (
(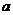 ≠0,
≠0,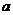 ,b,c是常数)中,自变量
,b,c是常数)中,自变量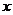 与函数y的部分对应值如下表:
与函数y的部分对应值如下表:
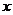
…
一l
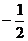
0
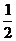
1
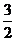
2
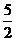
3
…
y
…
一2
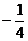
l
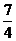
2
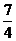
1
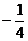
―2
…
(1)求该二次函数的解析式;
(2)说明二次函数图象的开口方向,并写出它的顶点坐标及对称轴;
(3)在如图所示的坐标系中画出显示其数量特征的抛物线草图;
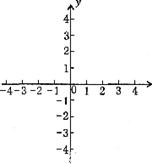
(4)求抛物线与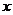 轴交点的坐标;
轴交点的坐标;
(5)当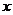 为多少时,函数取得最大(或最小)值,其最大(或最小)值是多少?
为多少时,函数取得最大(或最小)值,其最大(或最小)值是多少?
(6)写出不等式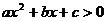 的解集.
的解集.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com